
|
1. Функциональная полнота системы булевых функций. Булевы функции. СДНФ, СКНФ. Теорема о функциональной полноте. Примеры функционально полных базисов.
Функция
Булеву функцию от n переменных можно задать таблицей истинности:
|
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
Существенные и не сущ переменные
Булевые
ф-и
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Для
ф-и
Булевы функ одной переменной
|
Простой конъюнкцией называется конъюнкция одной или нескольких переменных, при этом каждая переменная встречается не более одного раза (либо сама, либо ее отрицание).
Например,
![]() является простой конъюнкцией,
является простой конъюнкцией,
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.
Например,
выражение ![]() является ДНФ.
является ДНФ.
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные данного списка (либосами, либо их отрицания), причем в одном и том же порядке.
Например,
выражение ![]() является ДНФ, но не СДНФ. Выражение
является ДНФ, но не СДНФ. Выражение
![]() является СДНФ.
является СДНФ.
Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.
Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная входит не более одного раза (либо сама, либо ее отрицание).Например,
выражение ![]() – простая дизъюнкция,
– простая дизъюнкция,
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций (например
выражение ![]() – КНФ).
– КНФ).
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.
Например,
выражение ![]() является СКНФ.
является СКНФ.
Приведем алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы:
а) переход от ДНФ к КНФ
Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:
![]()
Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки;
б) переход от КНФ к ДНФ
Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения)
![]()
Таким образом, получили ДНФ.
Обратный переход (от СДНФ к ДНФ) связан с проблемой минимизации ДНФ. Подробнее об этом будет рассказано в разд. 5, здесь же мы покажем, как упростить ДНФ (или СДНФ) по правилу Блейка. Такая ДНФ называется сокращенной ДНФ;
в) сокращение ДНФ (или СДНФ) по правилу Блейка
Применение этого правила состоит из двух частей:
-
если среди дизъюнктных слагаемых в ДНФ
имеются слагаемые ![]() ,
то ко всей дизъюнкции добавляем
слагаемое К1К2.
Проделываем эту операцию несколько раз
(можно последовательно, можно одновременно)
для всех возможных пар слагаемых, а
затем, применяем обычное поглощение;
,
то ко всей дизъюнкции добавляем
слагаемое К1К2.
Проделываем эту операцию несколько раз
(можно последовательно, можно одновременно)
для всех возможных пар слагаемых, а
затем, применяем обычное поглощение;
-
если добавляемое слагаемое уже содержалось
в ДНФ, то его можно отбросить совсем,
например, ![]()
или
![]()
Разумеется,
сокращенная ДНФ не определяется
единственным образом, но все они содержат
одинаковое число букв (например, имеется
ДНФ ![]() ,
после применения к ней правила Блейка
можно прийти к ДНФ, равносильной данной):
,
после применения к ней правила Блейка
можно прийти к ДНФ, равносильной данной):
![]()
в) переход от ДНФ к СДНФ
Если
в какой-то простой конъюнкции недостает
переменной, например, z,
вставляем в нее выражение ![]() ,после
чего раскрываем скобки (при этом
повторяющиеся дизъюнктные слагаемые
не пишем). Например:
,после
чего раскрываем скобки (при этом
повторяющиеся дизъюнктные слагаемые
не пишем). Например:

г) переход от КНФ к СКНФ
Этот
переход осуществляется способом,
аналогичным предыдущему: если в простой
дизъюнкции не хватает какой-то переменной
(например, z,
то добавляем в нее выражение ![]() (это не меняет самой дизъюнкции), после
чего раскрываем скобки с использованием
распределительного закона):
(это не меняет самой дизъюнкции), после
чего раскрываем скобки с использованием
распределительного закона):
![]()
Таким образом, из КНФ получена СКНФ.
Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.
Будем использовать логическую функцию “эквивалентность”, записанную в виде ху. Напомним, что 00= 1; 01=0; 10= 0; 11= 1.Таким образом, ху = 1 тогда и только тогда, когда х = у.
Лемма. Любая логическая функция f(x1, x2, …, xn) может быть представлена в виде дизъюнкции 2п дизъюнктных слагаемых, причем дизъюнкция берется по всевозможным наборам из En.Этот факт будем записывать следующим образом:
![]() (*)
(*)
где дизъюнкция проводится по всевозможным наборам (s1, s2, …, sп) из Еп.
Доказательство леммы.
а)
Пусть f(x1, x2, …, xn)=
1. Тогда слева в формуле (* ) стоит 1.
Докажем, что и справа в этом случае стоит
1, для чего достаточно указать одно
дизъюнктное слагаемое, равное 1. Но среди
всех наборов (s1,
s2, …,
sп)
имеется набор s1 = х1,
s2 = х2, …,
sп = хп.
Очевидно, что для этого набора слагаемое
![]() равно
1 (так как и
равно
1 (так как и ![]() .
.
б) Пусть f(x1, x2, …, xn) = 0. Предположим, что справа стоит не ноль, а единица, тогда какое-то слагаемое тоже должно равняться 1, т. е. для некоторого набора
![]()
Это
означает (по свойствам конъюнкции), что
![]() ,
откуда следует, что х1=1,
х2=,…, хп=n,
но в этом случае f ( 1, n) f(x1,x2, …,xn)
= 0 и, значит, справа нет слагаемого,
равного 1, т. е. в этом случае и справа
и слева в формуле (* ) стоит 0. Лемма
доказана.
,
откуда следует, что х1=1,
х2=,…, хп=n,
но в этом случае f ( 1, n) f(x1,x2, …,xn)
= 0 и, значит, справа нет слагаемого,
равного 1, т. е. в этом случае и справа
и слева в формуле (* ) стоит 0. Лемма
доказана.
Теорема. Если булева функция не равна тождественному нулю, то ее можно представить в виде СДНФ по ее таблице истинности следующим образом: берем только те наборы переменных(х1,х2, …,хn), для которых f(х1,х2, …,хn)
=1, и составляем простую конъюнкцию для этого набора так: если хi = 0, то берем в этой конъюнкции![]() , если хi =
1, то берем хi. Составляядизъюнкцию этих простых конъюнкций, придем к СДНФ.
, если хi =
1, то берем хi. Составляядизъюнкцию этих простых конъюнкций, придем к СДНФ.
Доказательство. Пусть f(x1,x2,…,xn) не равна тождественному нулю, тогда в дизъюнкции можно не записывать слагаемые, равные нулю, а из формулы (* ) следует следующее представление для данной функции

Запись
означает, что дизъюнкция берется по
всем наборам ( 1, n) , для которых
f ( 1, n) = 1.
Так как ![]() (если 1=0),
из формулы (**) следует утверждение
теоремы.
(если 1=0),
из формулы (**) следует утверждение
теоремы.
Следствие. Любую логическую (булеву) функцию можно выразить через три логические функции: конъюнкцию, дизъюнкцию и отрицание.
Из
предыдущей теоремы видно, что следствие
верно для любой функции, не равной
тождественному нулю. Однако
если f(x1, x2,…, xn)
=0,
то ее также можно выразить через
конъюнкцию, дизъюнкцию и отрицание,
например, так: f(x1, x2,…, xn)
= x1![]() ,и,
несмотря на то, что последнее выражение
не является простой конъюнкцией (и,
значит, не является СДНФ), тем не менее
тождественный ноль также выражен через
нужные три функции.
,и,
несмотря на то, что последнее выражение
не является простой конъюнкцией (и,
значит, не является СДНФ), тем не менее
тождественный ноль также выражен через
нужные три функции.
Набор функций, через которые можно выразить любые другие функции, называется полным набором (более точные формулировки даны в разд. 7). Таким образом, конъюнкция, дизъюнкция иотрицание являются полным набором.
По
аналогии с представлением любой функции
(не равной тождественному нулю) в виде
СДНФ можно функцию (не равную тождественной
1) представить в виде
СКНФ: простая дизъюнкциясоставляется для тех наборов переменных (х1, х2, …, хп), для которых f(x1, x2,…, xn)
= 0, причем если хi =
1, то в этой дизъюнкции берем ![]() , если же хi =
0, то берем хi.
, если же хi =
0, то берем хi.
Пример. Составить для импликации и сложения по модулю 2 СДНФ и СКНФ.
|
х
|
у
|
х у |
х + у |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
Тогда СДНФ для этих функций:
![]()
СКНФ для этих функций:
![]()
Полиномы Жегалкина
Полиномом (многочленом) Жегалкина от п переменных называется функция
P = a0 + a1x1 +a2x2 + ...anxn +an +1x1x2 +...+an +C2nxn-1xn + ...+a2n-1x1x2..xn
Всего здесь 2п слагаемых. Напомним, что + сейчас означает сложение по модулю 2, коэффициенты a0, a1,..., a2n-1 являются константами (равными нулю или единице).
Теорема. Любая функция п переменных может быть представлена полиномом Жегалкина и это представление единственно.
Доказательство. Любая функция f(x1, x2, …, xn) имеет свою таблицу истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределенными коэффициентами. Затем по очереди подставляем всевозможные наборы переменных и находим коэффициенты. Легко видеть, что за каждую подстановку находим только один коэффициент. Так как число наборов равно числу коэффициентов (и равно 2п), отсюда следует утверждение теоремы.
Доказательство этой теоремы показывает, как по таблице истинности построить полином Жегалкина.
Имеется
2-й способ нахождения полинома Жегалкина
для функций, заданных в
виде ДНФ.
Этот способ основан на том, что х+1
= ![]() .
Если функция задана в виде ДНФ, то сначала
убираем дизъюнкцию, используя при этом
правило де Моргана, а все отрицания
заменяем прибавлением единицы. После
этого раскрываем скобки по обычным
правилам, при этом учитываем, что четное
число одинаковых слагаемых равно нулю
(так как х+
х =
0), а нечетное число одинаковых слагаемых
равно одному такому слагаемому.
.
Если функция задана в виде ДНФ, то сначала
убираем дизъюнкцию, используя при этом
правило де Моргана, а все отрицания
заменяем прибавлением единицы. После
этого раскрываем скобки по обычным
правилам, при этом учитываем, что четное
число одинаковых слагаемых равно нулю
(так как х+
х =
0), а нечетное число одинаковых слагаемых
равно одному такому слагаемому.
Пример.
![]() (
xy + 1)((x + 1)(y + 1) + 1)((y + 1)z + 1) + 1 = (xy + 1)(xy + x +
y)(yz + z + 1) + 1 = (x + y)(yz + z + 1) + 1= xyz + yz + xz +yz + x +
y + 1 = xyz + xz + x +y + 1.
(
xy + 1)((x + 1)(y + 1) + 1)((y + 1)z + 1) + 1 = (xy + 1)(xy + x +
y)(yz + z + 1) + 1 = (x + y)(yz + z + 1) + 1= xyz + yz + xz +yz + x +
y + 1 = xyz + xz + x +y + 1.
Последнее выражение и есть полином Жегалкина данной функции.
Функция f (x1,x2,…,xn) называется линейной, если ее полином Жегалкина содержит только первые степени слагаемых. Более точно функция называется линейной, если ее можно представить в виде
f(x1, x2, …, xn) = a0 + a1 x1 + a2 x2 +…+ an xn.
Класс линейных функций часто обозначают через L. (Заметим, что число линейных функций п переменных равно 2п+1).
Замечание. Если
пі 2 то
линейная функция в таблице истинности может
содержать только четное число
единиц. Действительно,
если f(x1,x2,…, xn)
= x1+
x2+…+xn, то
легко видеть что такая функция в таблице
истинности содержит одинаковое число
нулей и единиц а именно 2п /2
единиц и нулей, т. е. число это четно
при пі 2.
Столько же нулей и единиц имеет функция
![]() . Добавление же фиктивной переменной
приводит к
увеличению числа единиц (и нулей) в два
раза. Разумеется, нелинейная функция
может иметь в таблице истинности как
четное, так и нечетное число единиц.Одна
из сфер применения булевых функций —
синтез логических схем; при этом булевым
функциям соответствуют определённые
функциональные элементы (детали). Полнота
системы функций означает, что, пользуясь
только элементами соответствующих этим
функциям типов, можно собрать любую
логическую схему. При схемной реализации
константы 0 и 1 специальных элементов
не требуют. Поэтому существует ослабленное
понятие функциональной полноты.
. Добавление же фиктивной переменной
приводит к
увеличению числа единиц (и нулей) в два
раза. Разумеется, нелинейная функция
может иметь в таблице истинности как
четное, так и нечетное число единиц.Одна
из сфер применения булевых функций —
синтез логических схем; при этом булевым
функциям соответствуют определённые
функциональные элементы (детали). Полнота
системы функций означает, что, пользуясь
только элементами соответствующих этим
функциям типов, можно собрать любую
логическую схему. При схемной реализации
константы 0 и 1 специальных элементов
не требуют. Поэтому существует ослабленное
понятие функциональной полноты.
Определение.
Система функций S называется полной в
слабом смысле, если система ![]() является
полной (в сильном смысле, т. е. в смысле
определения в пункте 1).
является
полной (в сильном смысле, т. е. в смысле
определения в пункте 1).
Теорема 1. (Пост). Для того, чтобы система функций S была полной в слабом смысле необходимо и достаточно, чтобы она содержала хотя бы одну нелинейную функцию и хотя бы одну немонотонную функцию.
Теорема 2. (Пост). Для того, чтобы система функций была полной (в сильном смысле) необходимо и достаточно, чтобы она не содержалась целиком ни в одном из замкнутых классов K0, K1, KS, KM и KL.
Схема доказательства. Необходимость очевидна, поскольку никакой из перечисленных классов не совпадает целиком с множеством всех булевых функций.
Достаточность доказывается в 3 этапа:
построение
констант 0 и 1 с помощью функций ![]() ,
, ![]() и
и ![]() ;
построение функции–отрицания с помощью
констант 0, 1 и функции
;
построение функции–отрицания с помощью
констант 0, 1 и функции ![]() ;
построение конъюнкции с помощью констант
0, 1, функции
;
построение конъюнкции с помощью констант
0, 1, функции ![]() и
и ![]() .
.
После этого учитывая, что дизъюнкция представляется через конъюнкцию и отрицание
![]() и
что система
и
что система ![]() полная,
достаточность доказана.
полная,
достаточность доказана.
Замечание. Из теоремы, в частности, следует, что всякий замкнутый класс, отличный от множества всех булевых функций, содержится в одном из классов K0, K1, KS, KM, KL. По этой причине перечисленные классы называют основными замкнутыми классами пространства булевых функций.
Пример.
Рассмотрим совокупность булевых
функций ![]() .
Составим и заполним следующую таблицу,
отмечая знаком «+» функции, принадлежащие
соответствующим классам. Заполнение
первых трех строчек очевидно. Кроме
того, непосредственно видно, что
функция
.
Составим и заполним следующую таблицу,
отмечая знаком «+» функции, принадлежащие
соответствующим классам. Заполнение
первых трех строчек очевидно. Кроме
того, непосредственно видно, что
функция ![]() сохраняет
константы 0 и 1. Уже по форме записи она
является линейной. Самодвойственоость
функции
сохраняет
константы 0 и 1. Уже по форме записи она
является линейной. Самодвойственоость
функции ![]() вытекает
из таблицы значений (см. на следующей
странице), а монотонность очевидна
из диаграммы Хассе.
вытекает
из таблицы значений (см. на следующей
странице), а монотонность очевидна
из диаграммы Хассе.
Из
таблицы видно, что множество функций S
не содержится полностью ни в одном из
пяти основных замкнутых классов (нет
ни одного столбца целиком заполненного
символами «+»). Следовательно, система
функций S является полной (в сильном
смысле), а совокупность ![]() –
полная в слабом смысле.
–
полная в слабом смысле.
2 . Основные понятия теории графов.
Основные определения. Псевдограф. Мультиграф. Ориентированный граф. Мар-
шрут, цепь, цикл. Связные графы. Изоморфные графы. Гамильтоновы графы. Эйлеровы
графы. Независимые множества и клики. Представления графов.
Конечным
графом наз тройка Г=(X,U,Ф),
где х-конечное мн-во вершин, U-конечное
мн-во ребер(дуг), Ф-отношение инцидентности,
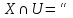 .
Отношение инцидентности Ф яв-ся трехмерным
отнешением Ф(x,u,y),где
х
.
Отношение инцидентности Ф яв-ся трехмерным
отнешением Ф(x,u,y),где
х
 ,
которое может выполся(быть истин), либо
не выполн(быть ложным) и удовлетворяют
св-ам:
,
которое может выполся(быть истин), либо
не выполн(быть ложным) и удовлетворяют
св-ам:
-
 -
ребро всегда соединяет пару вершин
-
ребро всегда соединяет пару вершин -
 -ребро
и соответствует не более чем одной паре
вершин x,y.
-ребро
и соответствует не более чем одной паре
вершин x,y.
Граф представл графов
|
Элементы графов |
Геом обьекты |
|
х
|
Точка в пространстве |
|
|
Направл отрезок |
|
|
отрезок |
|
|
Замкн отрезок |
 и
и
 н-ся изоморфными
(
н-ся изоморфными
( ),
если существуют 2 взаимно однозна
соответсвия
),
если существуют 2 взаимно однозна
соответсвия
 и
и
 сохр отношение инцидентности:
сохр отношение инцидентности: где
где
 ,
,
 .
Из определения следует, что изоморфные
графы можно одинаково изображать
графически и отличатся они будут только
метками вершин.
.
Из определения следует, что изоморфные
графы можно одинаково изображать
графически и отличатся они будут только
метками вершин.
Граф
наз-ся ориентированным(орграф),
если каждое его ребро ориентировано: .
Иногда удобно преобразовать неориент
граф в ориентир- заменой каждого неоринт
ребра парой ориент ребер с противоп
ориентацией.
.
Иногда удобно преобразовать неориент
граф в ориентир- заменой каждого неоринт
ребра парой ориент ребер с противоп
ориентацией.
Подграфом
графа
Г=(X,U,Ф)
наз такой граф Г’=(X’,U’,Ф),что
 .
Обозначают Г’
.
Обозначают Г’ Г
Г
Граф
наз псевдографом,
если в нем допускаются петли и кратные
ребра, т. Е. 2 вершины могут быть соединены
более чем одним ребром. Псевдограф без
петель наз мультиграфом.


Неориент граф нся простым, если он не имее петель и любая пара вершин соединена не более чем оним ребром.
Простой
граф
нся полным, если каждая пара вершин
соединена ребром. Такой граф с n
вершинами содержит
 ребер.
ребер.
Дополнением
простого графа
Г наз граф
 ,
имеющий те же вершины, а его ребра яв-ся
дополнением Г до полного графа.
,
имеющий те же вершины, а его ребра яв-ся
дополнением Г до полного графа.
Граф
наз плоским(планарным)
если он может быть изображен на плоскости
так, что все пересечения ребер яв-ся его
вершинами.

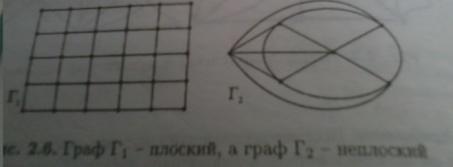
 Если
вершины x
и y
соед. ребром u,
то говорят, что вершины x
и y
смежные, а ребро u
инцидентно вершинам x
и y.
Два ребра наз смежными,
если они имеют общую вершину.
Если
вершины x
и y
соед. ребром u,
то говорят, что вершины x
и y
смежные, а ребро u
инцидентно вершинам x
и y.
Два ребра наз смежными,
если они имеют общую вершину.
Степенью вершины графа наз количество ребер, инцидентно данной вершине. Вершина графа, имеющая степень 0, наз изолированной, а если степень равна 1, то висячей.
Граф нся помеченным(или пронумер)если его вершины отличаются друг от друга каким –либо пометками.
Пусть
(маршрут) на графе Г=(X,U,Ф)
определяется последовательностью
вершин и ребер
 ,
где
,
где
 Ребро
Ребро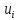 соед вершину
соед вершину
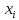 с
вершиной
с
вершиной
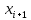 т.е.
выполняется отношение инцидентности
т.е.
выполняется отношение инцидентности

Маршрут наз цепью, если все его ребра различные.
Маршрут
наз замкнутым, если

Замкнутая цепь назыв циклом.
Цепь наз простой, если не содержит одинаковых вершин.
Простая замкнутая наз простым циклом.
Гамильтоновой цепью наз простая цепь, содержащей все вершины графа.
Гамильтоновым циклом наз простой цикл, содерж все вершины графа.
Граф
Г=(X,U,Ф)
наз связным,
если для всех
 существует путь из вершины х в вершину
у(вершины х и у связанны маршрутом).
Связанный ориентированный граф нся
сильно
связным.
Орграф
наз слабо связанным, если соответсвующий
ему неориентированный граф(игнорируется
ориентацией ребер) связный.
существует путь из вершины х в вершину
у(вершины х и у связанны маршрутом).
Связанный ориентированный граф нся
сильно
связным.
Орграф
наз слабо связанным, если соответсвующий
ему неориентированный граф(игнорируется
ориентацией ребер) связный.
Связный неориент ациклический граф нся деревом, мн-ва деревьев нся лесом.
Эйлеровы графы.
Пусть Г=(X,U,Ф)-неор псевдограф. Цепь в Г назся эйлеровой, если она проходит по одному разу через каждое ребро псевдографа Г. Такой граф назся эйлеровым. Замкнутая эйлерова цепь назся эйлеровым циклом.
Теорема Эйлера
Эйлерова цепь в псевдографе Г=(X,U,Ф) существует ТиТТК вып след условия:
-
Граф связный
-
Степени внутренних вершин четные(внутр вершины не явся началом и концом цепи)
-
Если вершины a и b явся началом и концом цепи и a ≠ b, то степени их не четны
-
Если вершины a и b явся началом и концом цепи и a = b, то их степени четные.
Вывод если граф содержит более 2 вершин то граф будет не эйлеровой
НЕ зависимые мн-ва и клики
Пусть Г=(X,U,Ф) –ориент или неор граф
Подмнож-во
Д=х нся доминирующим
мн-ва графа,
если каждая не
 Д-вершина
явся конечной вершиной некот ребра от
вершины
Д-вершина
явся конечной вершиной некот ребра от
вершины
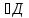 .
.
Минимальным доминирующим мн-ом нся такое доминирующее мнво что никакое его подмнво не обладает этим свом
Числом
доминирования
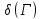 графа
нся наименьшее число вершин составляющее
м/п доминирующее мнво.
графа
нся наименьшее число вершин составляющее
м/п доминирующее мнво.
Пусть
Г=(X,U,Ф)
неор и без петель I Xнся
независимым,
если м/у любыми его вершинами нет
соединяющих ребер.
Xнся
независимым,
если м/у любыми его вершинами нет
соединяющих ребер.
В зависимом мнве хотя бы 2 вершины соединены ребром.
Мнво Q нся полностью зависимым, если каждая его пара вершин соединена ребром.
Вершина графа составляющая Q, образует полный подграф.
Максим незав мнво есть незав мнво, которое становится зависимым после добавления к нему любой вершины.
Заметим, что каждая незав мнво содержится в некот мак незав мнве.
Макс
число
 вершин
составляющих независ-е мнво нся числом
вершиной независимого графа.
вершин
составляющих независ-е мнво нся числом
вершиной независимого графа.
Определение незав мнва ребер
Подобно незав мнва вершин рассм незав мнва ребер, сост из ребер, не имеющ общих вершин.
Макс число ребер в макс незав мнве нся числом ребер независимости графов
Пример:


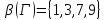 =4
=4
Независ
мн-во мах
когда оно доминирующе, а значит

Клика есть полностью завис мнво, которое теряет это свво после добавления к нему любой вершины.
Замеч!!!
Если
F=(x,u,ф)-простой,
то полностью зависим-е мнва(клики) в Г
становятся мах незав мнве в дополнит
графе
 .
Верно и обратное.
.
Верно и обратное.
 1,2,3-клика.5-4,4-3
клика
1,2,3-клика.5-4,4-3
клика

 ,
где
,
где
 называются функциями
алгебры логики, или булевыми фукциями.
Множество булевых функций от n
переменных обозначим
называются функциями
алгебры логики, или булевыми фукциями.
Множество булевых функций от n
переменных обозначим
 ,
где
,
где
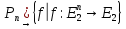 .
.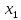
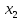

 .Если
число переменных n,
то в табл. Истинности имеется
.Если
число переменных n,
то в табл. Истинности имеется
 строк. Следовательно всего разл ф-ий
составляет
строк. Следовательно всего разл ф-ий
составляет
 ,
то есть
,
то есть

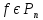 существенно зависит от переменной
существенно зависит от переменной
 ,
если существует такой набор значений
,
если существует такой набор значений
 что
что
 в
этом случае
в
этом случае
 -сущ
перемен,
в противном
-сущ
перемен,
в противном
 наз-ют не
сущ перем
(фиктивной). Пример:
наз-ют не
сущ перем
(фиктивной). Пример: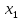

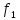
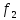
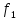
 -не
сущ перм, а
-не
сущ перм, а
 -сущ.
-сущ.
 -вершина
-вершина
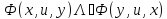 ориен
ребро, дуга
ориен
ребро, дуга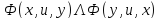 неориент
ребро
неориент
ребро петля
петля