Раздел 1. Элементы векторной алгебры в пространстве

Тема 1.1.Направленные отрезки. Векторы.

Сложение и вычитание векторов

Литература: [1], §§ 1-4, стр. 1-5; [2], §§ 2-4, стр. 10-14.

Основные определения, теоремы и формулы

Отрезок называется направленным, если указаны его начало и конец. Если A – начало, а B – конец направленного отрезка, то такой направленный отрезок обозначается так: .

Два направленных отрезка называются эквипаллентными, если они одинаково направлены и имеют равные длины.

Например, пусть ABCD – квадрат. Тогда направленные отрезкииэквиполлентны,ине эквиполлентны, они имеют одинаковые длины, но разные направления.

Вектор – это множество направленных отрезков, любые два из которых эквиполлентны. Вектор обозначается одной буквой, над которой ставится стрелка: . Если направленный отрезок- представитель вектора, то направленный отрезок вполне определяет весь класс ему эквиполлентных направленных отрезков. Поэтому если, то векторобозначают также через.

Возьмем произвольные векторы и . От какой-нибудь точки А отложи вектор=, а затем от точки В отложим вектор. Векторназываетсясуммой векторов и и обозначается так:. Это правило сложения векторов называетсяправилом треугольника: +=.

Иногда векторы удобно складывать поправилу параллелограмма, например, на приведенном ниже рисунке сумма векторов найдена по правилу параллелограмма: .

Теорема: Для произвольных векторов ,исправедливы следующие равенства:

1. (свойство коммутативности)

2. (свойство ассоциативности)

Разностью двух векторов иназывается вектортакой, что+=. Разность векторов иобозначается-. По правилу треугольника=-.

Вопросы для самоконтроля

1. Как определяется прямое произведение двух множеств?

2. Что такое отношение  на множестве М?

3. Какие можете привести примеры отношений на множестве?

4. Какое отношение называется отношением эквивалентности? Приведите примеры отношений, которые:

а) являются,

б) не являются

отношением эквивалентности.

5. Какой отрезок называется направленным?

6. Какие направленные отрезки называются эквиполлентными? Какие отрезки будут не эквиполлентными?

7. Сформулируйте и докажите признак эквивалентности направленных отрезков.

8. Что такое вектор? Нуль-вектор? Какие величины в природе изображаются векторами? Является ли векторной величиной: 1) работа; 2) объем; 3) вес? Если да, то куда эта величина направлена?

9. Сформулируйте и докажите лемму о равенстве векторов.

10. Сформулируйте и докажите утверждение об откладывании вектора от точки.

11. Как определяется сумма двух векторов? Покажите на чертеже.

12. Докажите коммутативность сложения векторов.

13. Докажите ассоциативность сложения векторов.

14. В чем смысл “правила многоугольника”?

Пример 1. Показать, что если для любых трех векторов ,иимеет место равенство, то из их представителей можно составить треугольник.

Решение.Равенство согласно правилу сложения векторов означает, что если начало векторасовместить с концом вектора, а начало вектора- с концом вектора, то конец векторасовместится с началом вектора, т.е. ломанная, составленная из векторов замкнется, образуя треугольник.

Задание: Нарисуйте три вектора, из которых нельзя составить треугольник.

Пример 2. Пусть АВСD параллелограмм, и О – точка пересечения его диагоналей, M – середина стороны AD. Полагая и, выразить черезивекторы, и.

Решение.По правилу многоугольника для сложения векторов имеем:;;;и др.

Из возможных способов выберем тот, при котором из точки А можно прийти в точку В, двигаясь только по известным векторам. В данном случае выбираем способ:

. Так как , то. Аналогично находим:.

.

Задачи

1. В параллелограмме ABCD диагонали пересекаются в точке O. Указать, какие из следующих пар направленных отрезков эквиполлентны: а) и; б)и; в)и; г)и.

2. Доказать, что направленные отрезки AB и CD эквиполлентны тогда и только тогда, когда середины отрезков AD и BC совпадают.

3. Диагонали параллелограмма ABCD пересекаются в точке O, а точки E и F – соответственно середины отрезков BC и AD. Построить следующие векторы:

а)

4. Доказать, что для произвольных векторов исправедливо равенство- (-)=+.

5. Даны параллелограмм ABCD и произвольная точка O пространства. Доказать, что

6. Даны три точки A, B и C. Построить точку P такую, чтобы .

7. A, B, C и D – произвольные точки пространства, M и N – середины отрезков AD и BC. Доказать, что 2. Какие можно вывести следствия из последнего утверждения?

8. Доказать, что для произвольных векторов исправедливы следующие соотношения: а). При каком условии в этих соотношениях имеет место знак равенства?

9. Что можно сказать о векторах, для которых выполнено соотношение: а)   (-); б) (+)‌ ‌-?

10. Треугольники ABC и AB₁C₁ имеют общую медиану AM. Доказать, что в этом случае

11. Записать в векторной форме необходимое и достаточное условие того, что четырехугольник ABCD – параллелограмм.

Задачи повышенной трудности

1. В пространстве дана фигура, состоящая из конечного числа точек, симметричных относительно точки C. Доказать, что сумма всех векторов с общим началом и концами в точках данной фигуры равна нулевому вектору тогда и только тогда, когда общим началом векторов является точка C.

2. В выпуклом пятиугольнике ABCDE BC║AD, CD║BE, DE║AC, AE║BD. Доказать, что AB║CE.

3. Периметр пятиугольника равен I. Строятся последовательно пятиугольники с вершинами в серединах сторон предыдущих пятиугольников. Доказать, что сумма периметров всех этих пятиугольников не больше 8.

Домашнее задание

1. Пусть A, B, C, D – произвольные точки пространства, а M, N, P, Q – соответственно середины отрезков AB, BC, CD, DA. Доказать, что направленные отрезки MH QP эквиполлентны.

2. Точки M, H – середины ребер AA₁ и BB₁ параллелепипеда ABCDA₁B₁C₁D₁ с центром O. Построить следующие векторы:

3. Доказать, что если для четырех точек A, B, C, D, не лежащих на одной прямой, и некоторой точки O пространства имеет место равенство то ABCD – параллелограмм.

4. Доказать, что для любых векторов 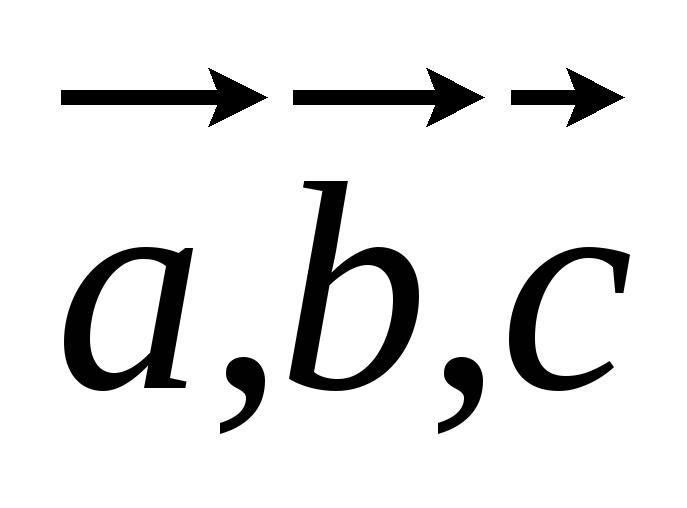справедливо соотношение