
- •Практические занятия по геометрии
- •1 Семестр
- •Раздел 1. Элементы векторной алгебры в пространстве
- •Тема 1.1.Направленные отрезки. Векторы.
- •Тема 1.2.Умножение векторов на действительные числа
- •Тема 1.3.Коллинеарные и компланарные векторы.
- •Тема 1.4.Скалярное произведение векторов
- •Тема 1.5.Векторные подпространства
- •Тема 1.6.Применение векторов к решению задач
- •Задачи повышенной трудности
- •Домашнее задание
- •Индивидуальные задания по векторной алгебре Вариант I
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
Тема 1.4.Скалярное произведение векторов
Литература: [1], § 8, стр. 25-28; [2], §8, стр. 30-31.
Основные определения, теоремы и формулы
Скалярным
произведением двух векторов называется
число, равное произведению их длин на
косинус угла между ними. Скалярное
произведение векторов
![]() и
и![]() обозначается через
обозначается через![]() .
Итак, по определению
.
Итак, по определению![]() .
.
Теорема.
Для произвольного числа
![]() и произвольных векторов
и произвольных векторов![]() и
и![]() справедливы следующие равенства:
справедливы следующие равенства:
1)
![]() ,
,
2)
![]() и
и![]() ,
,
3)
![]()
Если
известны координаты векторов
![]() и
и![]() относительно ортонормированного базиса,
то скалярное произведение этих векторов
равно сумме произведений их одноименных
координат, то есть, если
относительно ортонормированного базиса,
то скалярное произведение этих векторов
равно сумме произведений их одноименных
координат, то есть, если![]() (
(![]() ),
),![]() (
(![]() ),
то
),
то
![]() =
=![]() ,
,
и
угол между этими векторами можно
определить по формуле:
![]() .
.
Вопросы для самоконтроля
1. Дать определение угла между векторами.
2. чему равен угол между векторами, если хотя бы один из векторов нулевой?
3. Какой можно сделать вывод, если:
1)
![]() =0;
2)
=0;
2)![]() <0;
3)
<0;
3)![]() >0?
>0?
4. Для каждого из случаев, приведенных в п.3 сформулируйте обратные утверждения. Справедливы ли они?
5. В чем состоит геометрический смысл координат вектора в ортонормированном базисе?
6. Сравните свойства скалярного произведения векторов со свойствами умножения чисел. Перечислите общие свойства этих произведений. Какими свойствами умножения чисел скалярное произведение не обладает? Объясните почему.
7. Пусть
![]() =
=![]() .
Следует ли отсюда, что
.
Следует ли отсюда, что![]() ?
?
Пример
1. Доказать,
что вектор
![]() ортогонален вектору
ортогонален вектору![]() .
.
Решение.
Два
вектора ортогональны тогда и только
тогда, когда их скалярное произведение
равно нулю. Вычислим скалярное произведение
векторов![]() и
и![]() :
:
![]() ·
·![]() =
=![]()
Следовательно,
векторы
![]() и
и![]() ортогональны.
ортогональны.
Пример
2. Треугольник
АВС задан векторами
![]()
![]() и
и![]() .
Выразить через векторы
.
Выразить через векторы![]() и
и![]() вектор
вектор![]() ,
гдеAH
–
высота треугольника.
,
гдеAH
–
высота треугольника.
Р ешение.
Выразим вектор
ешение.
Выразим вектор
![]() через векторы
через векторы![]() и
и![]() :
:![]() =
=![]() +
+![]() =
=![]() +
+![]() .
Так как вектор
.
Так как вектор![]() коллинеарен вектору
коллинеарен вектору![]() ,
то
,
то![]() .
Тогда
.
Тогда![]() =
=![]() +
+![]() .
Для нахождения величины
.
Для нахождения величины![]() воспользуемся перпендикулярностью
векторов
воспользуемся перпендикулярностью
векторов![]() и
и![]() .
Так как они перпендикулярны, то
.
Так как они перпендикулярны, то![]()
![]() =0,
т. е. (
=0,
т. е. (![]() +
+![]() )(
)(![]() =0.
Отсюда
=0.
Отсюда![]() и
и![]() =
=![]() +
+![]()
![]() .
.
Задачи
Вычислить скалярное произведение векторов
 =3
=3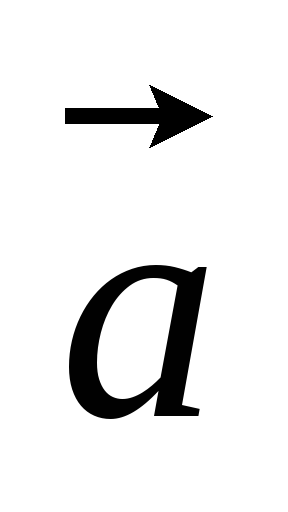 -2
-2 и
и =
= +2
+2 ,
если векторы
,
если векторы и
и образуют
угол φ=
образуют
угол φ= и
и
 .
.Вычислить скалярное произведение векторов
 =3
=3 -2
-2 и
и =
= +2
+2 ,
если известны координаты векторов
,
если известны координаты векторов и
и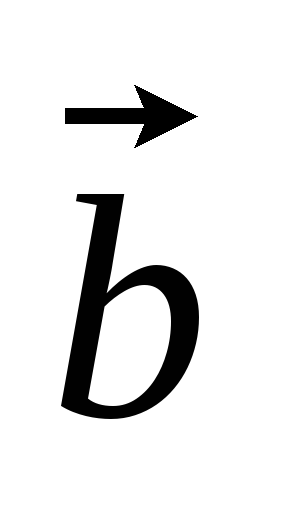 в ортонормированном базисе:
в ортонормированном базисе: (4,-2,-4),
(4,-2,-4), (6,-3,2).
(6,-3,2).В ортонормированном базисе даны векторы
 и
и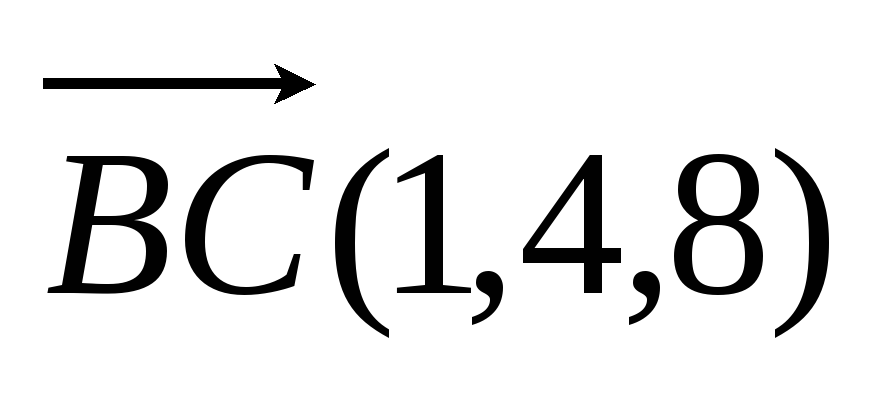 .
Найти: 1)cos
.
Найти: 1)cos ,
, .
.Известно, что векторы
 ,
, ,
, ненулевые и вектор
ненулевые и вектор не ортогонален векторам
не ортогонален векторам и
и .
При каком условии выполняется равенство
.
При каком условии выполняется равенство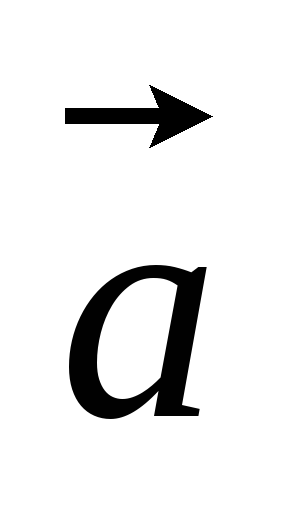 ·
· =
= ·
·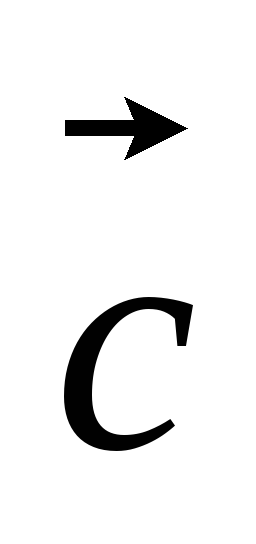 ?
?В пространстве даны три некомпланарных вектора
 ,
, и
и .
Найти вектор
.
Найти вектор ,
удовлетворяющий условиям:
,
удовлетворяющий условиям: ·
· =0,
=0, ·
· =0,
=0,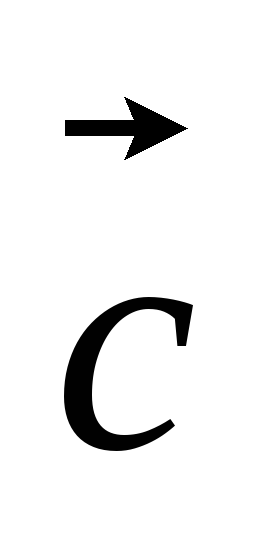 ·
·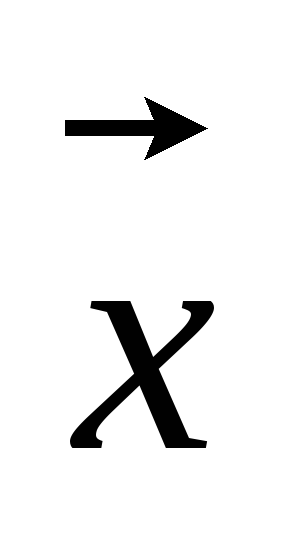 =0.
=0.Какие из следующих равенств являются верными для любых входящих в них векторов: а)

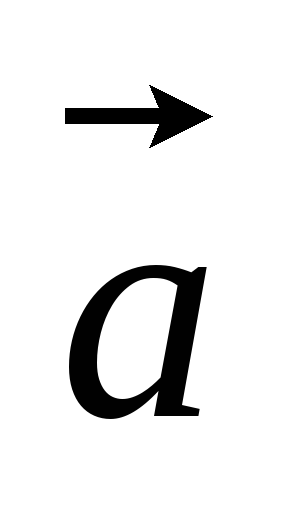 =
= ;
б) (
;
б) (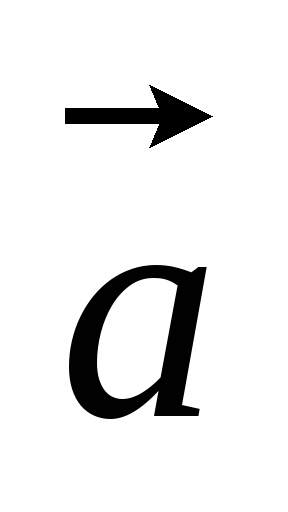 +
+ )2=
)2= +2
+2 ·
· +
+ ;
в) (
;
в) ( ·
· )2=
)2= +
+ ;
;
г)
(![]() ·(
·(![]() ·
·![]() )
-
)
-![]() ·(
·(![]() ·
·![]() ))·
))·![]() =0.
=0.
Какой угол образуют единичные векторы
 и
и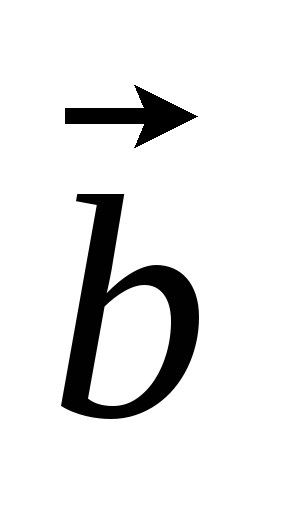 ,
если известно, что векторы
,
если известно, что векторы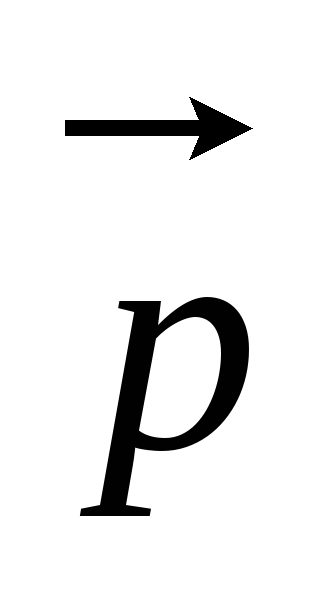 =
= +2
+2 и
и =5
=5 -4
-4 взаимно перпендикулярны?
взаимно перпендикулярны?Вычислите внутренние углы треугольника ABC и убедитесь, что треугольник равнобедренный, если
 и
и .
.Вычислите тупой угол, образованный медианами, проведенными из вершин острых углов равнобедренного прямоугольного треугольника.
Дан параллелограмм ABCD. Дать геометрическое истолкование равенств: 1) (
 )2
–
(
)2
–
( -
- )2=4
)2=4 ·
· ;
;
2)
(![]() +
+![]() )2
+ (
)2
+ (![]() -
-![]() )2=2(
)2=2(![]() 2+
2+![]() 2);
3) (
2);
3) (![]() )(
)(![]() -
-![]() )=
)=![]() 2-
2-![]() 2.
2.
Задачи повышенной трудности
Дан тетраэдр SABC. Известны координаты векторов
 ,
, и
и в ортонормированном базисе. Найти
высотуSH
этого тетраэдра.
в ортонормированном базисе. Найти
высотуSH
этого тетраэдра.Доказать, что из пяти векторов всегда можно выбрать два так, чтобы длина их суммы не превосходила длину суммы оставшихся трех векторов.
Указание: попробуйте рассуждать методом от противного.
На окружности радиуса 1 с центром в точке O дано 2n+1 точек A1, A2, … , A2n+1, лежащих по одну сторону от некоторого диаметра. Доказать, что
 .
.
Указание: воспользуйтесь методом математической индукции.
Домашнее задание
Доказать, что ABCD – квадрат, если векторы

 и
и
 в ортонормированном базисе имеют
следующие координаты:
в ортонормированном базисе имеют
следующие координаты: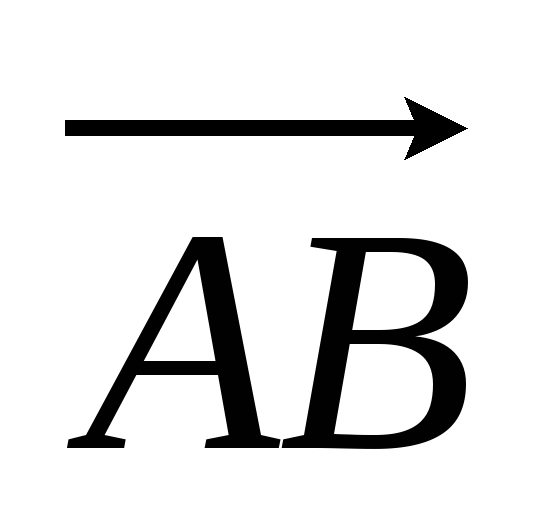 (3,5,4),
(3,5,4),
 (-4
(-4
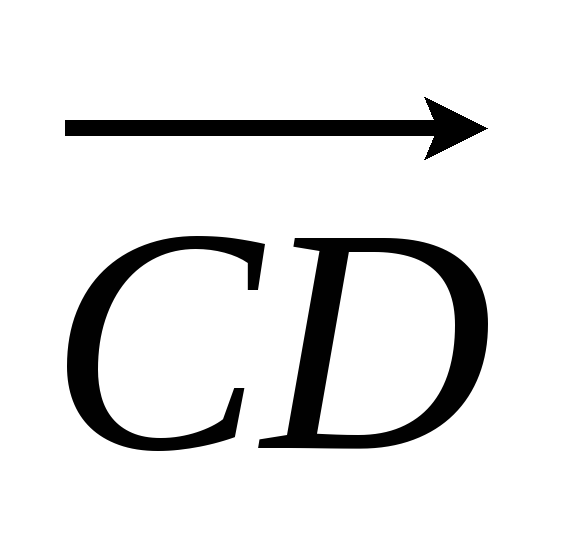 (-3,-5,-4).
(-3,-5,-4).Вектор
 образует с векторами
образует с векторами и
и ортонормированного базиса
ортонормированного базиса ,
, ,
, соответственно углы 1200
и 1350.
Найти угол, который образует вектор
соответственно углы 1200
и 1350.
Найти угол, который образует вектор
 с ортом
с ортом .
.ABCD – параллелограмм. Доказать, что диагонали параллелограмма ABCD перпендикулярны, если в ортогональном базисе
![]() (0,6,-2),
(0,6,-2),
![]() (6,3,-1).
(6,3,-1).
