
- •Практические занятия по геометрии
- •1 Семестр
- •Раздел 1. Элементы векторной алгебры в пространстве
- •Тема 1.1.Направленные отрезки. Векторы.
- •Тема 1.2.Умножение векторов на действительные числа
- •Тема 1.3.Коллинеарные и компланарные векторы.
- •Тема 1.4.Скалярное произведение векторов
- •Тема 1.5.Векторные подпространства
- •Тема 1.6.Применение векторов к решению задач
- •Задачи повышенной трудности
- •Домашнее задание
- •Индивидуальные задания по векторной алгебре Вариант I
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
Тема 1.2.Умножение векторов на действительные числа
Литература: [1], §5, стр. 14-16; [2], §§ 2-4, стр. 14-19.
Основные определения, теоремы и формулы
Произведением
вектора
![]() на действительное
(вещественное) число
на действительное
(вещественное) число
![]() называется вектор
называется вектор![]() =
=![]()
![]() ,
который удовлетворяет следующим
условиям:
,
который удовлетворяет следующим
условиям:
1)
![]() ,
где
,
где![]() абсолютное значение числа
абсолютное значение числа![]() ,
,
2)
![]() ,
если
,
если![]() и
и![]() ,
если
,
если![]() <0.
<0.
Теорема:
Для
произвольных чисел
![]() и векторов
и векторов![]() справедливы следующие равенства:
справедливы следующие равенства:
1)
![]() и
и![]() ,
,
2)
![]() ,
,
3)
![]() ,
,
4)
![]() .
.
Вопросы для самоконтроля
1.
В каких случаях
![]()
![]() равно
равно
![]() ?
?
2.
Что можно сказать о векторах
![]() и
и![]() ,
если известно, что уравнение
,
если известно, что уравнение![]() :
1) имеет единственное решение; 2) не имеет
решений; 3) имеет бесчисленное множество
решений?
:
1) имеет единственное решение; 2) не имеет
решений; 3) имеет бесчисленное множество
решений?
3.
Пусть
![]() .
Следует ли отсюда, что
.
Следует ли отсюда, что![]() =
=![]() ?
?
Пример
1.
По данным векторам
![]() и
и![]() построить
векторы:
построить
векторы:
1)![]() ;
2)
;
2)![]() ;
;
Р ешение.Пусть
ешение.Пусть
![]() и
и![]() -
данные векторы (см. рисунок):
-
данные векторы (см. рисунок):
1)
Возьмем произвольную точку А пространства
и построим векторы
![]() и
и![]() .
Тогда согласно определению суммы
векторов вектор
.
Тогда согласно определению суммы
векторов вектор![]() .
.
2)
Возьмем произвольную точку М пространства
и построим векторы
![]() и
и![]() .
Тогда согласно определению разности
векторов
.
Тогда согласно определению разности
векторов![]() .
.
Задачи
Дан вектор
 .
Построить векторы: а)
.
Построить векторы: а) ;
б)
;
б) ;
в)
;
в) .
.Дано
 .
Каким условиям должны удовлетворять
числа
.
Каким условиям должны удовлетворять
числа и
и ,
чтобы точкаC
принадлежала: 1) прямой AB,
2) лучу AB,
3) отрезку AB?
,
чтобы точкаC
принадлежала: 1) прямой AB,
2) лучу AB,
3) отрезку AB?Записать с помощью векторов условие того, что четырехугольник ABCD является трапецией с основаниями AB и СD.
Точка M – середина отрезка AB, O – произвольная точка пространства. Доказать, что
 .
.В треугольнике ABC отрезки AM и AN являются соответственно медианой и биссектрисой внутреннего угла. Выразить векторы
 и
и через
векторы
через
векторы

 .
.Доказать, что если ABCDEF – правильный шестиугольник, то
 .
.Угол AOB меньше развернутого. Используя векторы
 и
и
 ,
найти вектор, параллельный биссектрисе
данного угла.
,
найти вектор, параллельный биссектрисе
данного угла.
Задачи повышенной трудности
Точка O пересечения диагоналей четырехугольника ABCD и M и N - середины его противоположных сторон AB и CD лежат на одной прямой. Доказать, что четырехугольник ABCD – трапеция или параллелограмм.
Даны правильный n – угольник A1, A2, … , An с центром O и произвольная точка M пространства. Доказать, что: а)
 б)
б) .
.Доказать, что точка M – центр тяжести треугольника ABC тогда и только тогда, когда выполняется равенство
 .
.
Домашнее задание
По данным векторам
 и
и построить векторы:
построить векторы:
а)
3![]() ;
б) -2
;
б) -2![]() +
+![]()
![]() .
.
Точка M – центр параллелограмма ABCD, а O – произвольная точка пространства. Доказать, что
 .
.В параллелепипеде ABCDA1B1C1D1 направленные отрезки, совпадающие с его ребрами, определяют векторы:
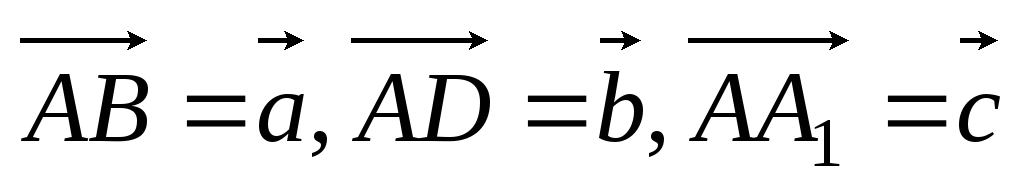 .
Построить каждый из следующих векторов:
а)
.
Построить каждый из следующих векторов:
а) +
+ -
-
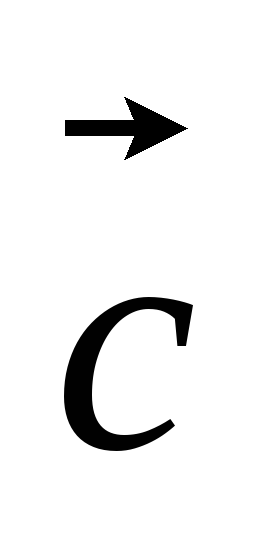 ;
б)
;
б)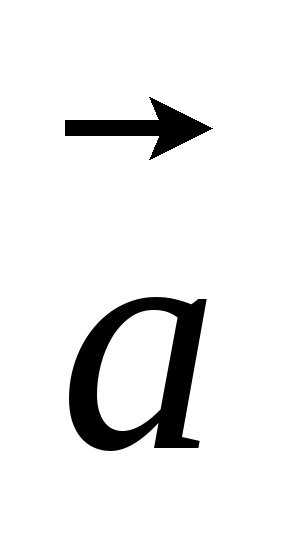 +
+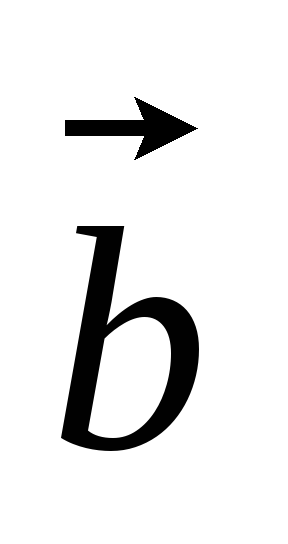 +
+ ;
в) -
;
в) -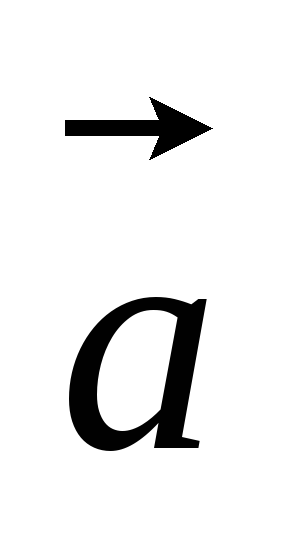 -
-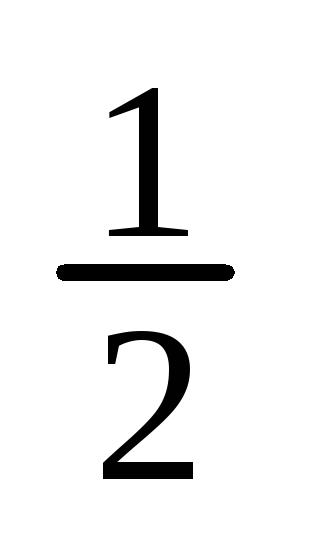
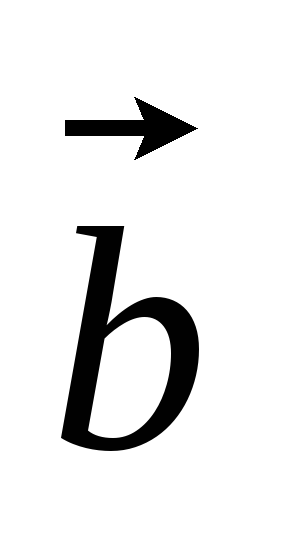 +
+ .
.Дан вектор
 ,
длина которого равна 3. Построить вектор
,
длина которого равна 3. Построить вектор ,
если его длина равна 5, и он направлен
противоположно вектору
,
если его длина равна 5, и он направлен
противоположно вектору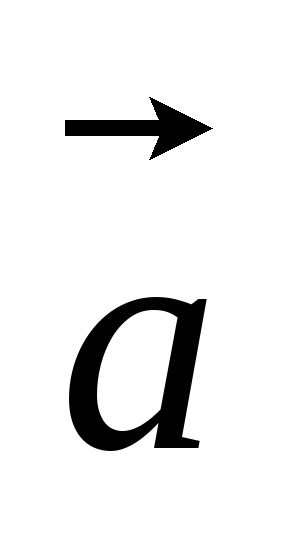 ,.
,.
Тема 1.3.Коллинеарные и компланарные векторы.
Линейная зависимость векторов. Координаты вектора в векторном пространстве.
Литература: [1], §§ 6-7, стр. 16-24; [2], §§ 6,7, стр. 19-25.
Основные определения, теоремы и формулы
Два вектора, параллельные одной прямой, называются коллинеарными. Два ненулевых коллинеарных вектора либо одинаково, либо противоположно направлены. Нулевой вектор считается коллинеарным любому вектору.
Теорема1:
Если
векторы
![]() и
и![]() коллинеарны и
коллинеарны и![]() ,
то существует единственное число
,
то существует единственное число![]() такое, что
такое, что![]() .
.
Векторы
![]() и
и![]() называютсякомпланарными,
если существует плоскость, которой они
параллельны.
называютсякомпланарными,
если существует плоскость, которой они
параллельны.
Теорема2:
Если
векторы
![]() и
и![]() компланарны, а векторы
компланарны, а векторы![]() не коллинеарны, то существуют единственные
числа
не коллинеарны, то существуют единственные
числа![]() и
и![]() такие, что
такие, что![]() .
.
Рассмотрим
систему векторов
![]() и зададимn
действительных чисел
и зададимn
действительных чисел ![]() . Вектор
. Вектор
![]()
называется
линейной
комбинацией данных
векторов
![]() .
.
Система
векторов
![]() называетсялинейно
зависимой,
если существуют числа
называетсялинейно
зависимой,
если существуют числа
![]() ,
среди которых хотя бы одно отлично от
нуля, и такие что
,
среди которых хотя бы одно отлично от
нуля, и такие что![]() .
.
Если
же равенство
![]() справедливо только при
справедливо только при![]() ,
то система векторов
,
то система векторов![]() называетсялинейно
независимой.
называетсялинейно
независимой.
Базисом векторного пространства называется система векторов, удовлетворяющая следующим трем условиям:
1) она упорядочена,
2) линейно независима,
3) всякий вектор пространства является линейной комбинацией векторов системы.
Число векторов базиса называется размерностью пространства.
Теорема
3.
Если векторы
![]() и
и![]() не компланарны, то для любого вектора
не компланарны, то для любого вектора![]() существуют единственные числа
существуют единственные числа![]() и
и![]() такие, что
такие, что![]() .
.
Пусть
B=(![]() )
– базис векторного пространства V и
)
– базис векторного пространства V и![]() V.
Если
V.
Если![]() ,
то числа
,
то числа![]() называютсякоординатами
вектора
называютсякоординатами
вектора
![]() относительно базиса B и записывают
относительно базиса B и записывают![]() (
(![]() ).
).
Теорема 4. Координаты суммы векторов равны сумме соответствующих координат слагаемых. При умножении вектора на число на это же число умножается каждая координата данного вектора.
Базис
B
называется ортонормированным,
если базисные векторы
![]() единичные и взаимно ортогональные
(перпендикулярные). Векторы ортонормированного
базиса обозначаются
единичные и взаимно ортогональные
(перпендикулярные). Векторы ортонормированного
базиса обозначаются![]() .
.
Теорема
5.
Длина вектора
![]() ,
заданного координатами в ортонормированном
базисе
,
заданного координатами в ортонормированном
базисе![]() вычисляется по формуле
вычисляется по формуле![]()
Вопросы для самоконтроля
1. Что такое подсистема системы векторов?
2. Если система векторов линейно независима, то, что можно сказать о подсистеме? Сформулируйте обратное утверждение. Справедливо ли обратное утверждение?
3. Векторы
![]() и
и![]() коллинеарны. Что можно сказать о
зависимости системы векторов
коллинеарны. Что можно сказать о
зависимости системы векторов![]() и
и![]() ?
?
4. Если векторы
![]() и
и![]() компланарны,
то можно ли утверждать, что система,
состоящая из векторов
компланарны,
то можно ли утверждать, что система,
состоящая из векторов![]() и
и![]() ,
линейно зависима?
,
линейно зависима?
5. Верно ли утверждение: «Если вектор
![]() коллинеарен вектору
коллинеарен вектору![]() ,
вектор
,
вектор![]() коллинеарен вектору
коллинеарен вектору![]() ,
то
,
то![]() коллинеарен
коллинеарен![]() »?
»?
6. Что можно сказать о координатах: 1) равных векторов; 2) противоположных векторов?
7. Может ли система, состоящая из одного вектора, быть: 1) линейно зависимой; 2) линейно независимой?
8. Дан вектор
![]() относительно базисаB=(
относительно базисаB=(![]() )
векторного пространстваV:
)
векторного пространстваV:
каковы координаты векторов
 относительно базисаB?
относительно базисаB?каковы координаты вектора
 относительно базисаB΄=(
относительно базисаB΄=(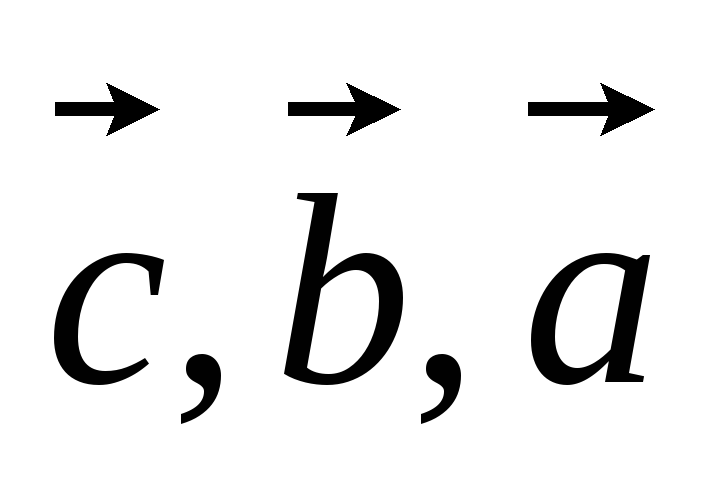 )?
)?
Пример 1.Даны неколлинеарные векторы![]() и
и![]() .
Коллинеарны ли векторы
.
Коллинеарны ли векторы![]() и
и![]() ?
?
Решение
1. В
разложении вектора
![]() вынесем за скобку
вынесем за скобку![]() :
:
![]() .
Тогда
.
Тогда
![]() ,
что свидетельствует о том, что векторы
,
что свидетельствует о том, что векторы![]() и
и![]() коллинеарны и противоположно направлены.
коллинеарны и противоположно направлены.
Решение
2. Неколлинеарные
векторы ![]() и
и![]() образуют
базис двумерного векторного пространства.
Коэффициенты в разложении векторов
образуют
базис двумерного векторного пространства.
Коэффициенты в разложении векторов![]() и
и![]() по векторам
по векторам![]() и
и![]() являются
координатами этих векторов в указанном
базисе. В этом базисе вектор
Так
как два вектора коллинеарны, если
соответствующие коэффициенты в их
разложениях по неколлинеарным векторам
пропорциональны, то, проверяя это условие
для векторов
являются
координатами этих векторов в указанном
базисе. В этом базисе вектор
Так
как два вектора коллинеарны, если
соответствующие коэффициенты в их
разложениях по неколлинеарным векторам
пропорциональны, то, проверяя это условие
для векторов
![]() и
и![]() :
:![]() ,
убеждаемся в их коллинеарности.
,
убеждаемся в их коллинеарности.
Решение
3. Чтобы
найти линейную зависимость между
векторами
![]() и
и![]() ,
надо из определяющих их равенств,
исключить векторы
,
надо из определяющих их равенств,
исключить векторы![]() и
и![]() .
Если этого сделать нельзя, то векторы
.
Если этого сделать нельзя, то векторы
![]() и
и![]() не коллинеарны.
не коллинеарны.
Из
первого разложения исключим вектор а:
![]() .
Из второго разложения исключим вектор
.
Из второго разложения исключим вектор![]() .
Тогда из последних равенств имеем
.
Тогда из последних равенств имеем![]() .
Отсюда:
.
Отсюда:![]() .
Что и свидетельствует о коллинеарности
векторов
.
Что и свидетельствует о коллинеарности
векторов![]() и
и![]() .
.
Пример
2. Из
точки О отложены два вектора
![]() и
и![]() .
Найти какой-нибудь вектор
.
Найти какой-нибудь вектор![]() ,
параллелный биссектрисе угла АОВ.
,
параллелный биссектрисе угла АОВ.
Решение.
Найдем
орты
![]() и
и![]() векторов
векторов![]() и
и
![]() .
Отложим их от точки O
и построим на них как на сторонах ромб.
Так как диагональ ромба делит его углы
пополам, то вектор
.
Отложим их от точки O
и построим на них как на сторонах ромб.
Так как диагональ ромба делит его углы
пополам, то вектор
![]() ,
направлен по биссектрисе угла АОВ.
,
направлен по биссектрисе угла АОВ.
П
 ример
3.
Даны три вектора
ример
3.
Даны три вектора
![]() (3,
-1 ),
(3,
-1 ),![]() (1,
-2 ),
(1,
-2 ),![]() (-1,
7). Определить разложение вектора
(-1,
7). Определить разложение вектора![]() по
базису
по
базису![]() ,
,![]() .
.
Решение.
Пусть
(![]() )
-
базис, в котором заданы координаты
векторов
)
-
базис, в котором заданы координаты
векторов
![]() ,
,![]() и
и![]() ,
и пусть
вектор
,
и пусть
вектор
![]() в этом базисе имеет координаты (p1,p2).
Зная координаты векторов
в этом базисе имеет координаты (p1,p2).
Зная координаты векторов
![]() ,
,![]() и
и![]() ,
найдем координаты вектора
,
найдем координаты вектора![]() :p1=
3 + 1 - 1, p2=
-1 -2 + 7 ), т. е.
:p1=
3 + 1 - 1, p2=
-1 -2 + 7 ), т. е.
![]() (
3, 4 ).
(
3, 4 ).
Е сли
и
-коэффициенты разложения вектора
сли
и
-коэффициенты разложения вектора
![]() по базису
по базису![]() ,
,![]() ,
то
,
то![]() =
=![]() +
+![]() .
Разложим векторы
.
Разложим векторы![]() ,
,![]() и
и![]() по векторам базиса (
по векторам базиса (![]() ):
):
![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() .
.
Тогда
![]() =
=![]() +
+![]()
![]() =
=
(![]() )
+
(
)
+
(![]() ).
).
Так
как два вектора равны тогда и только
тогда когда равны их соответствующие
координаты, то 3 = 3+,
4= -
- 2
, откуда =2
, =
-3. Тогда
![]() =2
=2![]() - 3
- 3![]() .
.
Пример
4. Разложить
ветер, идущий со скоростью 10 м/с с
северо-западного направления под углом
![]() к северу, на западную и северную
компоненты.
к северу, на западную и северную
компоненты.
Решение.
На
рисунке вектор
![]() - вектор скорости ветра, а векторы
- вектор скорости ветра, а векторы![]() и
и![]() -
его составляющие (восточная и южная )
компоненты. Так как АВСД - прямоугольник,
то
-
его составляющие (восточная и южная )
компоненты. Так как АВСД - прямоугольник,
то
![]() =
=
![]() sin
sin![]() = 5
= 5
![]()
= =
= =![]() сos
сos![]() =5
=5![]() .
Значит, восточная компонента
.
Значит, восточная компонента  равна
5 м/с, а южная 5
равна
5 м/с, а южная 5![]() м/с.
м/с.
Задачи
Доказать, что отношение коллинеарности векторов является отношением эквивалентности на множестве всех ненулевых векторов. Почему это отношение не будет отношением эквивалентности на множестве всех векторов?
Доказать, что если векторы
 и
и не коллинерны, то векторы
не коллинерны, то векторы
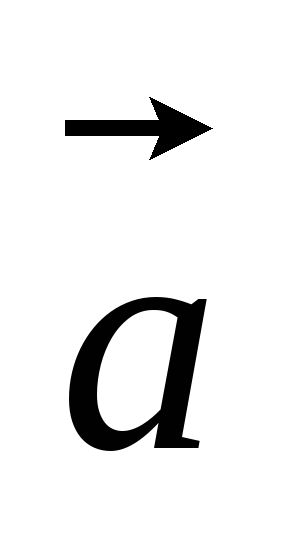 +
+ и
и =3
=3 -
- также не коллинеарны.
также не коллинеарны.Дан параллелепипед ABCDA1B1C1D1, точки P и F – середины ребер AD и AA1 соответственно. Выяснить, компланарны ли векторы: а)
 ;
б)
;
б)
 ;
в)
;
в)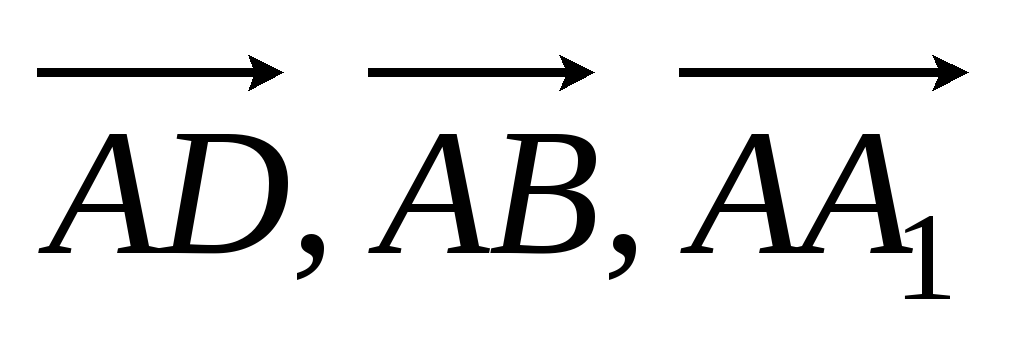 ;
г)
;
г) .
.Даны координаты трех векторов
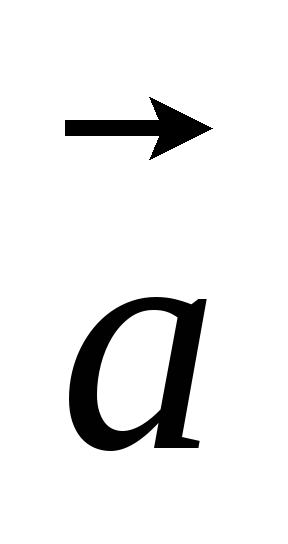 (-2,3,4),
(-2,3,4), (7,0,2)
и
(7,0,2)
и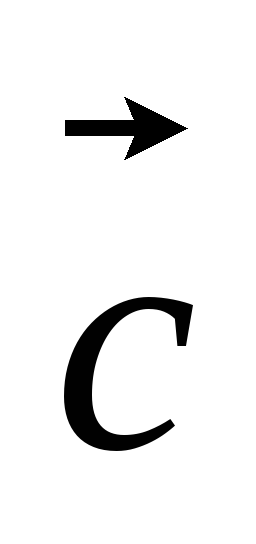 (-6,5,-1).
Найти координаты векторов
(-6,5,-1).
Найти координаты векторов
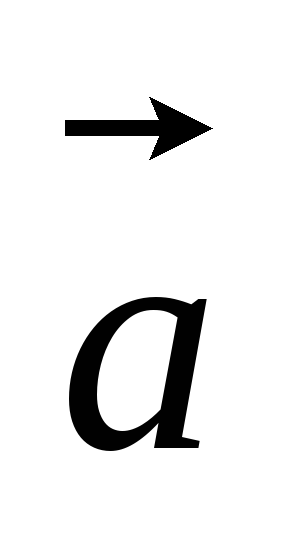 -3
-3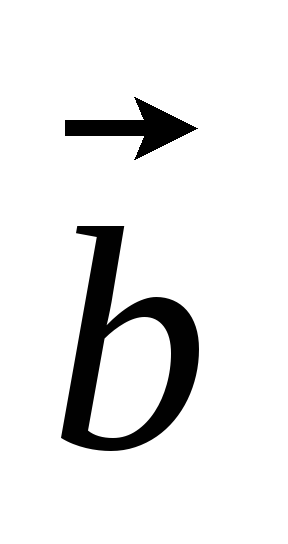 +
+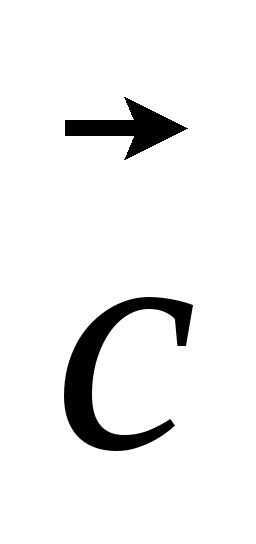 и
и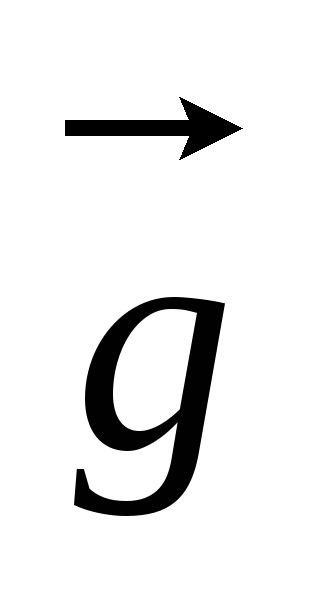 =4
=4 +5
+5 +3
+3 .
.Дана трапеция ABCD (
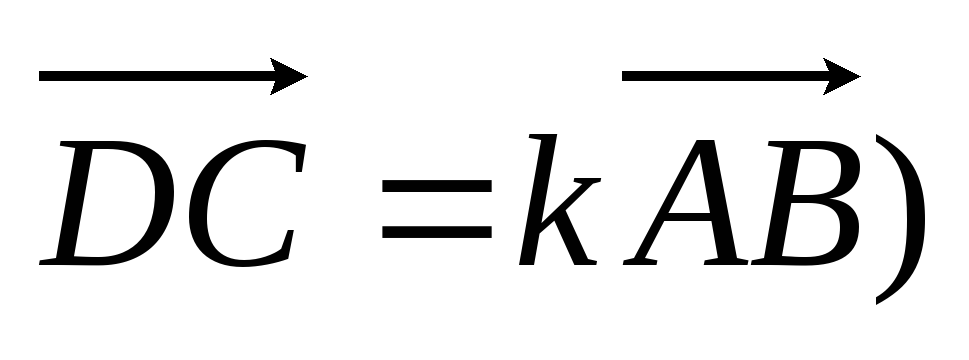 .
Точки M
и N
– середины оснований AB
и CD,
P
– точка пересечений диагоналей трапеции.
.
Точки M
и N
– середины оснований AB
и CD,
P
– точка пересечений диагоналей трапеции.
приняв векторы
 и
и
 за базисные, найти координаты векторов
за базисные, найти координаты векторов
 ;
;найти координаты векторов

Установить, какие из следующих троек векторов
 ,
, и
и линейно зависимы, и в тех случаях, когда
это возможно, представить вектор
линейно зависимы, и в тех случаях, когда
это возможно, представить вектор как линейную комбинацию векторов
как линейную комбинацию векторов и
и :
а)
:
а) (6,4,2),
(6,4,2), (-9,6,3),
(-9,6,3), (-3,6,3);
б)
(-3,6,3);
б) (5,2,1),
(5,2,1),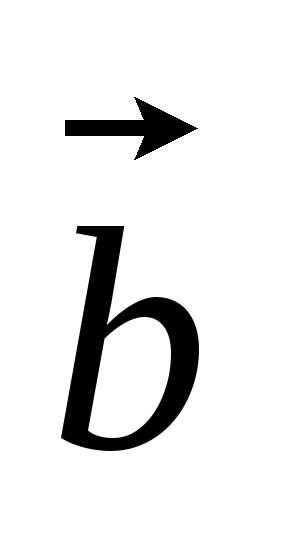 (-1,4,2),
(-1,4,2),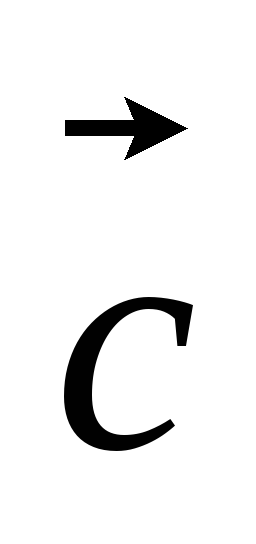 (-1,-1,6);
в)
(-1,-1,6);
в) (6,-18,12),
(6,-18,12), (-8,20,-16),
(-8,20,-16), (8,7,3).
(8,7,3).Среди векторов
 1(0,-3,0),
1(0,-3,0),
 2(-2,0,5),
2(-2,0,5),
 3(0,2,-1),
3(0,2,-1),
 4(0,0,4),
4(0,0,4),
 5(1,0,0),
5(1,0,0),
 6(0,1,-3),
6(0,1,-3),
 7(1,-2,7),
7(1,-2,7),
 8(0,0,0),
заданных в базисе (
8(0,0,0),
заданных в базисе ( ,
указать векторы: 1)коллинеарные
,
указать векторы: 1)коллинеарные ;
2) компланарные с векторами
;
2) компланарные с векторами и
и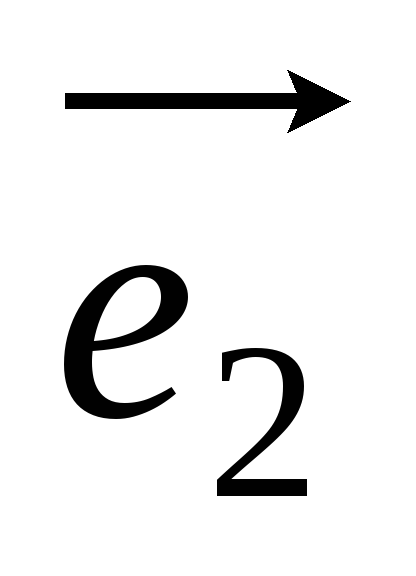 .
.Даны векторы
 ,
,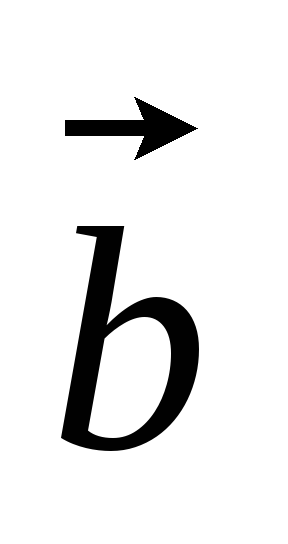 и
и .
Выяснить, являются ли они линейно
зависимыми, если: а)
.
Выяснить, являются ли они линейно
зависимыми, если: а) (-3,0,2),
(-3,0,2), (2,1,-4),
(2,1,-4), (3,-2,4);
б)
(3,-2,4);
б) (1,0,7),
(1,0,7), (-1,2,4),
(-1,2,4), (3,2,1);
в)
(3,2,1);
в) (5,-1,4),
(5,-1,4), (3,-5,2),
(3,-5,2), (-1,-13,-2).
(-1,-13,-2).Дана треугольная призма ABCA1B1C1. Приняв векторы
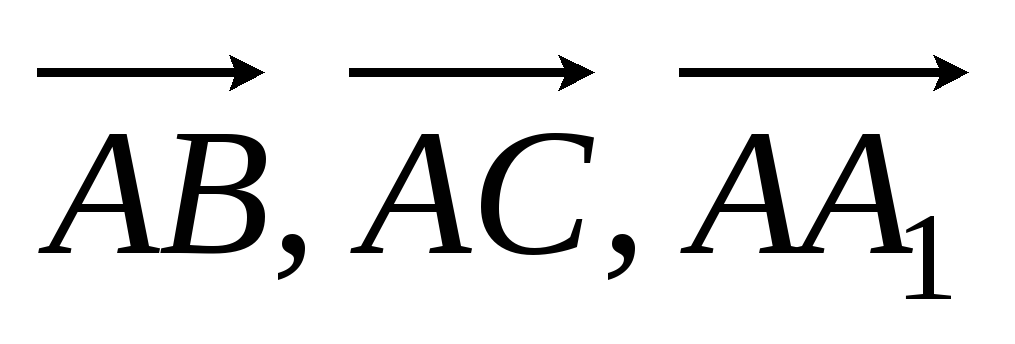 за базисные, найти координаты вектора
за базисные, найти координаты вектора
 ,
гдеM
– центр параллелограмма BCC1B1,
N
– центр тяжести треугольника A1B1C1.
,
гдеM
– центр параллелограмма BCC1B1,
N
– центр тяжести треугольника A1B1C1.
Задачи повышенной трудности
Доказать, что точка C лежит на прямой AB тогда и только тогда, когда существует такое число λ, что
 =
λ
=
λ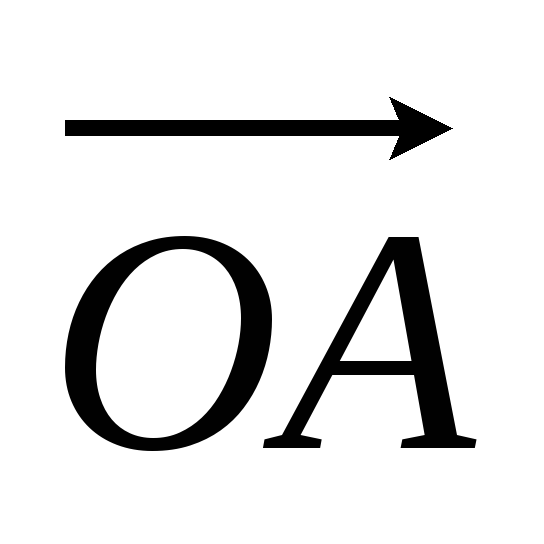 +(1-
λ)
+(1-
λ) .
.Доказать, что для любых векторов
 ,
, и
и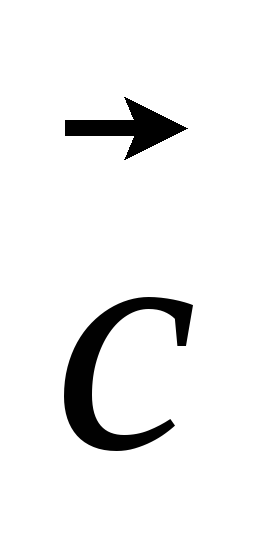 и чисел α, β и γ векторы α
и чисел α, β и γ векторы α - β
- β ,
γ
,
γ - α
- α ,
β
,
β - γ
- γ компланарны.
компланарны.Дана трапеция ABCD, у которой нижнее основание AB в два раза больше верхнего CD. Выразить векторы
 ,
, через
векторы
через
векторы
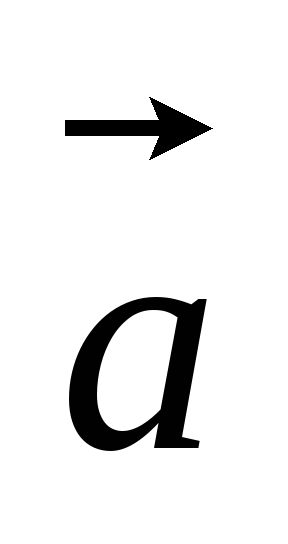 =
= и
и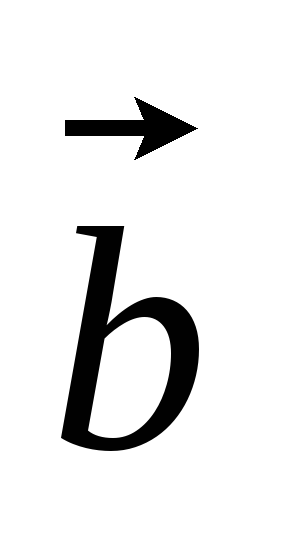 =
= .
.
Домашнее задание
Основанием пирамиды SABCD служит параллелограмм ABCD. Приняв векторы
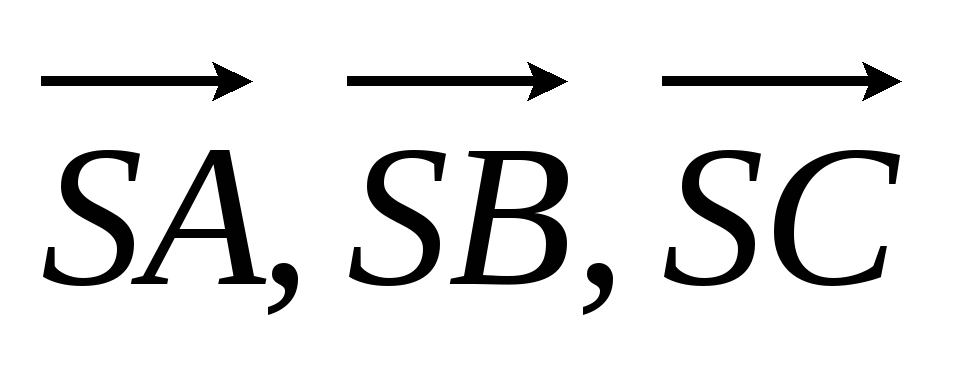 за базисные, найти координаты векторов
за базисные, найти координаты векторов
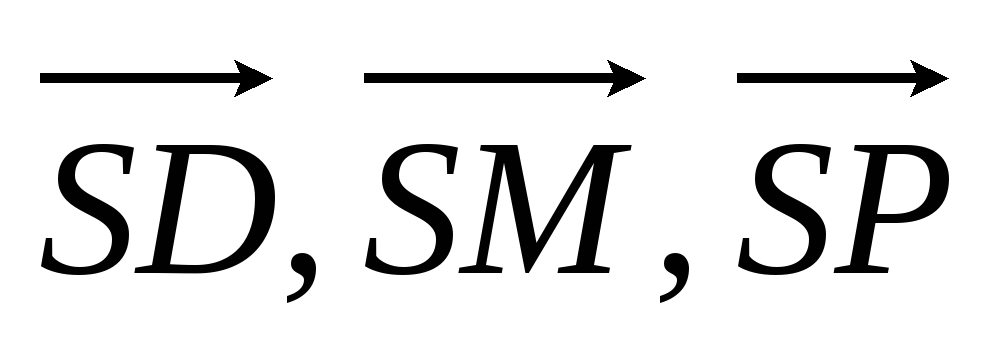 ,
, ,
где M
– середина отрезка AD
и (BC,P)=2.
((BC,P)=
,
где M
– середина отрезка AD
и (BC,P)=2.
((BC,P)= означает,
что
означает,
что
 ).
).Найти линейную зависимость между векторами: а)
 (1,3,0),
(1,3,0), (5,10,0),
(5,10,0), (4,-2,6);
(4,-2,6);
 (11,16,3);
б)
(11,16,3);
б)
 (2,3,1),
(2,3,1), (5,7,0),
(5,7,0), (3,-2,4);
(3,-2,4);
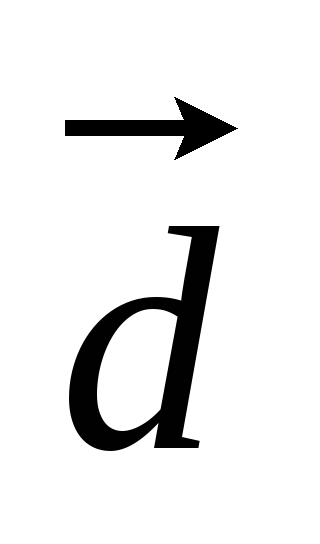 (4,12,-3);
в)
(4,12,-3);
в)
 (0,-3,4),
(0,-3,4), (5,2,0),
(5,2,0), (-6,0,1);
(-6,0,1);
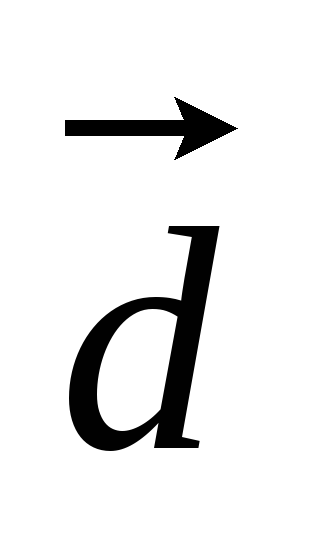 (25,-22,16).
(25,-22,16).Определить длины суммы и разности векторов
 и
и ,
если известны их координаты в
ортонормированном базисе:
,
если известны их координаты в
ортонормированном базисе: (3,-5,8),
(3,-5,8), (-1,1,4).
(-1,1,4).
