TауЦС_БФ_2013(2 семестр) / ЦСлекции / ЦСлекция02_прим
.docЛекция 2
Обратное
– преобразование
В отличии от известного преобразования Лапласа обратное
z
– преобразование не является однозначным.
Если z
– преобразование последовательности
определяется комплексной функцией
E(z),
то обратное z
– преобразование не обязательно будет
соответствовать e(t).
Результатом обратного z
– преобразования функции E(z)
является
последовательность {e(kT)},
которая совпадает с функцией e(t)
только в моменты квантования t
= kT.
k
= 0,1,2,…
Примером может служить единичная функция
y1
= 1(t)
и функция косинуса y2
= cos(t).
Проквантовав относительно времени t
с шагом T
= 2π, получим
абсолютно одинаковые последовательности
1(kT)
= cos(kT),
k
= 0,1,2,…, T
= 2π.
Неоднозначность обратного
z – преобразования является одним из ограничений при его применении.
Обратное z – преобразование будем обозначать
или
e(kT)
= ƺ-1[E(z)]
Определение. Обратным z – преобразованием комплексной функции E(z) будем называть последовательность соответствующих коэффициентов ряда Лорана разложения функции E(z)
2.1. Метод разложения в степенной ряд
Если z – преобразование E(z) представляет собой дробно – рациональную функцию, числитель и знаменатель которой есть алгебрагические полиномы от аргумента z, то коэффициенты ряда Лорана E(z)(1) могут быть получены делением числителя на знаменатель. Коэффициенты ряда соответствуют значению e(t) в момент квантования. Решением данного метода есть последовательность чисел e(kT), k = 0,1,2,…
Пример 1. Определить обратное z – преобразование функции
.
Решение.
Разделим полином числителя на полином знаменателя
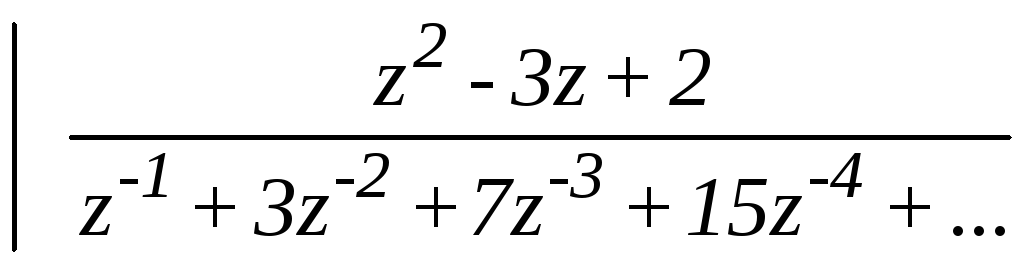
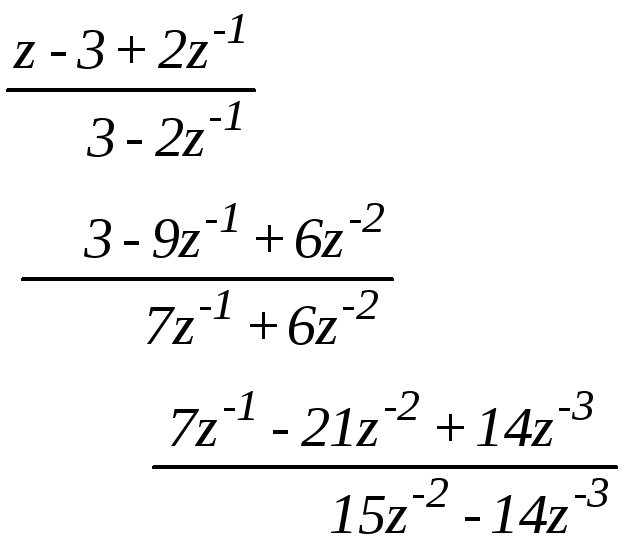
В результате деления получили следующие элементы числовой последовательности
Нетрудно записать элементы последовательности в общем виде (хотя эта операция не всегда удается)
.
Исходная функция
E(z)
имеет ряд
Лорана
Пример 2. Найдем обратное z – преобразование функции
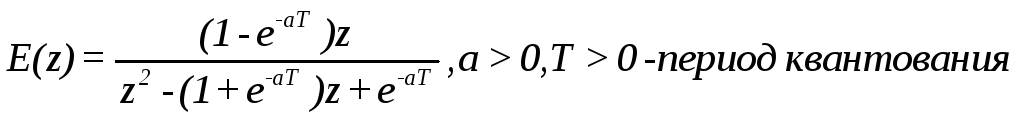
Решение.
Разделим числитель на знаменатель. Получим
2.2. Метод разложения на простое дроби
Данный метод похож на метод разложения на простые дроби в преобразовании Лапласа. Пусть функцию E(z) можно разложить на простые дроби
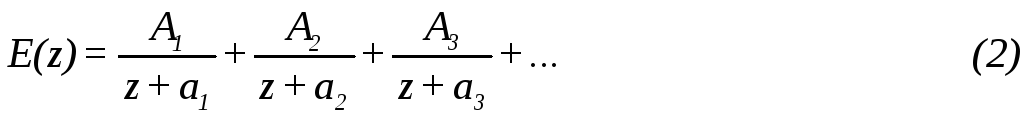
z – преобразования соответствующие слагаемым в выражении (2) отсутствуют ( смотри таблицу z – преобразований). Поэтому поступают следующим образом. На простые дроби раскладывается не функция E(z), а функция E(z)/z. Затем каждая дробь умножается на z, чтобы придать слагаемым в (2) надлежащую форму. После чего выражение E(z)/z умножается на z, т.е.
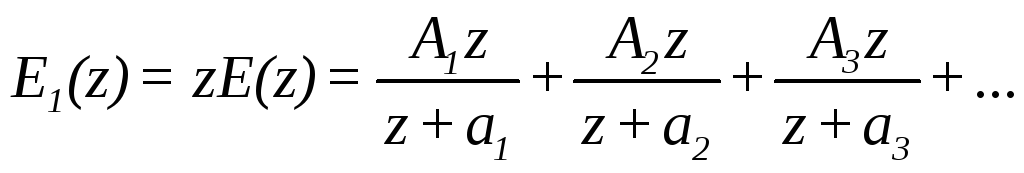
z – преобразование функции E(z) определяется
Пример
3.
Найдем обратное
–преобразование
для замкнутой формы
.
Решение.
Разложим
дробь
на
простые дроби
.
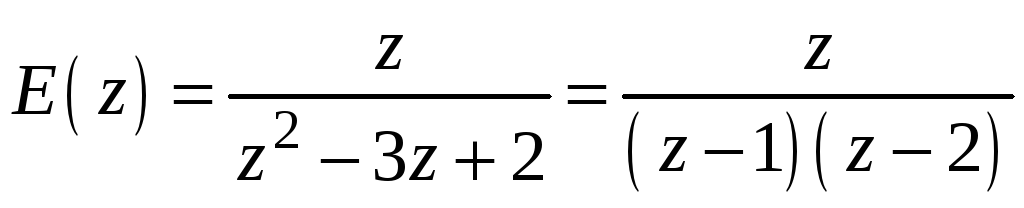Далее,
выражение состоящее из простих дробей
разделим на элемент
.
Будем иметь
.
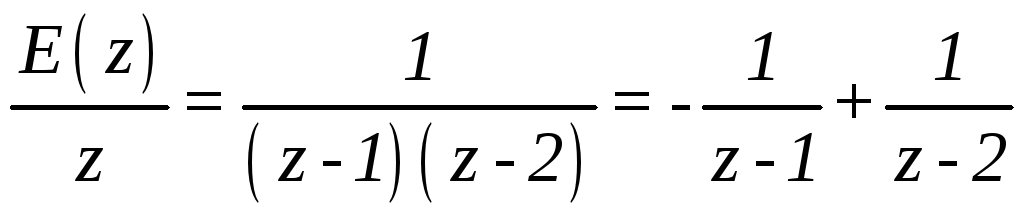Теперь
умножим полученную сумму, состоящей из
простых дробей, обратно на величину
и, воспользовавшись таблицей
–преобразований,
получим
.
Ответ аналогичен полученному методом разложения в степенной ряд.
Пример
4. Определим
–преобразование
для E(z)
из примера
2.
Решение. Разложим выражение E(z)/z на простые дроби
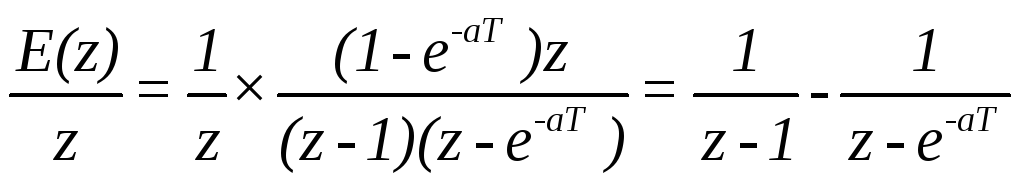
Окончательно получим
В
случае, когда E(z)
не содержит
в числителе множителя я и не имеет
полюсов
z = 0 то E(z) удобно представить в виде
Теперь функция F(z) имеет в числителе множитель z и решение задачи для последовательности ƒ(kT) может быть получено разложением F(z) на простые дроби. По теореме о сдвиге на целое число тактов получим
e(kT)= ƒ((k-1)T)
Далее если имеется полюс z = 0 кратности m, то можно поступить так
т.е., функция F(z) теперь содержит необходимый множитель z в числителе.
При использовании метода разложения на простые дроби полезна таблица z преобразований.
3.2. Общий метод нахождения обратного z – преобразования
Этот метод основывается на использовании известной в теории комплексного переменного формулы обращения.
Коэффициенты ряда Лорана функции E(z) можно определить с помощью соотношения
(6)
Известной как формула обращения, где Г окружность включающая полюсы
E(z). Данный интеграл (6) может быть определен по теореме вычетов
в полюсах E(z).
Выражение (6) является обратным z – преобразованием функции E(z).
Вычет в простом полюсе zi вычисляется по формуле
А вычет в полюсе zi кратности m
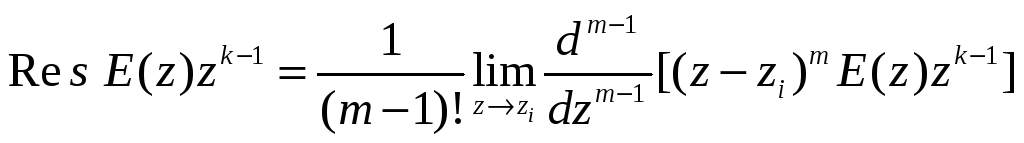
В том случае если E(z) дробно – рациональной функцией
,
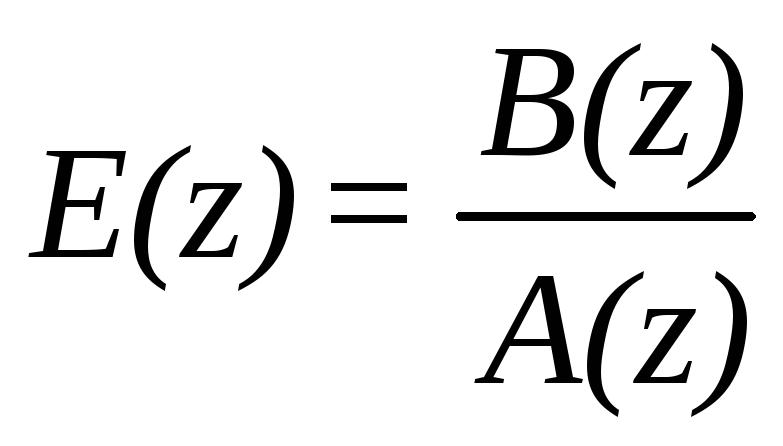где A(z) и B(z) алгебраические полиномы, причем степень полинома B(z) меньше степени полинома A(z), то элементы последовательности e(kT) определяются по формуле
где z – простые полюсы E(z) (корни характеристического уравнения A(z) = 0));
N – количество полюсов;
A/z – производная по z знаменателя функции E(z).
Пример. Найти обратное z – преобразование функции E(z) заданной в примере 4, использовав формулу обращения.
Решение. В соответствии с формулой обращения, получим
Г – окружность, которая включает простые полюсы z i= 1 и z2 = e-aT. По теореме вычетов имеем
Рассчитаем вычеты входящие в выражение
Первый вычет для z1 = 1
Второй вычет для z2 = e-aT
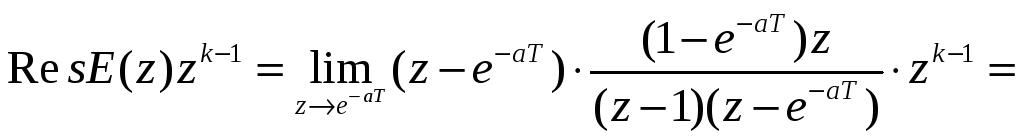
Следовательно
Пример. Пусть
теперь
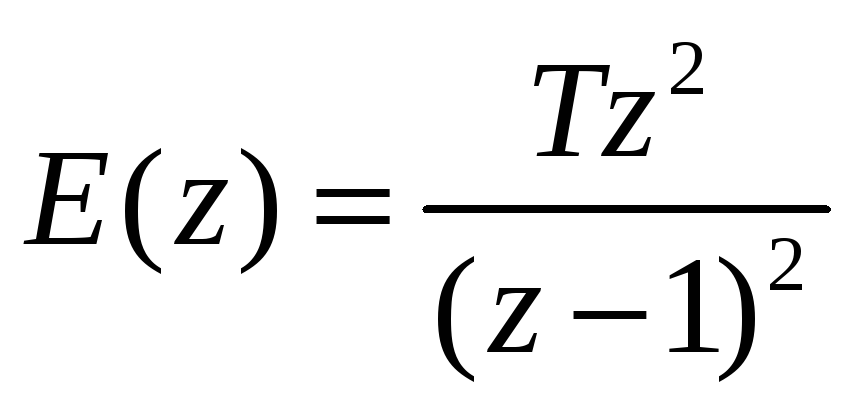. Найдем e(kT).
Решение. Функция E(z) имеет краткий полюс z1 = 1 кратности 2. Обратное
z – преобразование определится из соотношения
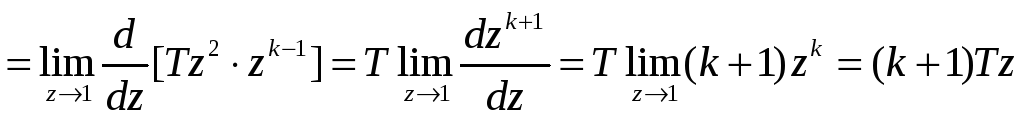
Для обратного z – преобразования получим
