Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный экономический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

17-11-2015_11-58-24 / Эконометрика (электронный конспект)

.pdf

Скачиваний:

Добавлен:

20.02.2016

Размер:

1.05 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Таким образом, задача свелась к решению системы уравнений (68), (71) относительно

векторов C и Λ:
2ΩC − X Λ = 2ω1:n,n+1 ,		(72)
X T C = XnT+1		(73)
Умножим уравнение (72) слева на Ω−1		и выразим из полученного равенства вектор C :
C = 1 Ω−1 X Λ + Ω−1ω		(74)
2	1:n,n+1
2
Подставим эту формулу в (73):
(X T Ω−1 X )Λ = 2(XnT+1 − X T Ω−1ω1:n,n+1 )		(75)
Отсюда:
Λ = 2(X T Ω−1 X )−1 (XnT+1 − X T Ω−1ω1:n,n+1 )		(76)
Подставим (76) в (74):
C = Ω−1 X (X T Ω−1 X )−1 (XnT+1 − X T Ω−1ω1:n,n+1 )+ Ω−1ω1:n,n+1			(77)

Формула (77) дает оптимальное решение оптимизационной задачи (67), (68). Следовательно, эффективный несмещенный прогноз вычисляется с помощью вектора (77) по формуле (56):

ˆ	= C	T	Y	(78)
Y	= C		Y	(78)
n+1

Из формул (5), (18), (19), (77) следует, что формула (78) может быть также представлена в виде:

ˆ		+ wn+1,1:nΩ	−1	(79)
Yn+1	= Xn+1b	+ wn+1,1:nΩ	e	(79)
Отметим,		что в случае классической модели		(когда Ω = I	n	)	b = b и	w		= 0 .
					n			1:n,n+1
							ˆ		= X	b ,
Следовательно, для случая классической модели формула (79) принимает вид: Y									= X	b ,
							n+1			n+1
что согласуется с полученными ранее результатами.

В случае, когда присутствует только гетероскедастичность (а автокорреляция отсутствует),

матрица Ω+ диагональна и w1:n,n+1		= 0 . Следовательно, в этом случае формула (79) имеет вид:
ˆ		(80)
Yn+1	= Xn+1b
Интервальная оценка для E[Yn+1 \|		X , Xn+1 ]
	Заметим, что в силу (52), (53):

E[Yn+1 | X , Xn+1 ]= Xn+1β

(81)

В силу несмещенности ОМНК-оценки b :

E X

| X , X

= X

(82)

n+1

Из результатов для классической модели следует,

что случайные величины b

и s2

независимы. Следовательно,

случайные величины X

b и

s2 также независимы. Поэтому в

n+1

силу (22’), (82) случайная величина:

b − X

n+1

t (Xn+1b)

σ(X

b | X

, X

)

(83)

n+1

(n − m)

n − m

имеет распределение Стъюдента со степенями свободы n − m .

Упростив (83), получим:

t (Xn+1b)

b − X

)

(84)

σ(X

b |

, X

n+1

Найдем стандартное отклонение σ(X

b | X , X

n+1

) случайной величины X

b .

n+1

var(Xn+1b | X , Xn+1 )= E Xn+1 (b −β)(b −β)T XnT+1 = Xn+1E (b −β)(b −β)T XnT+1 =

= Xn+1 var(b | X , Xn+1 )XnT+1

Итак,

var(Xn+1b | X , Xn+1 )= Xn+1 var(b | X , Xn+1 )XnT+1

(85)

Подставим (17) в (85):

var(Xn+1b | X , Xn+1 )= σ2 Xn+1 (X T Ω−1 X )−1 XnT+1

(86)

Из (86):

σ(Xn+1b | X , Xn+1) = σ

Xn+1 (X T Ω−1 X )−1 XnT+1

(87)

В силу (86), (87) в качестве оценок дисперсии и стандартного отклонения случайной

величины X

возьмем:

n+1

		2	Xn+1	(X	T	Ω	−1	X )	−1	T
var(Xn+1b \| X , Xn+1 )= s			Xn+1	(X		Ω		X )		Xn+1

s(Xn+1b | X , Xn+1) = s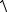Xn+1 (X T Ω−1 X )−1 XnT+1

Подставим (87) в формула (84):

(88)

(89)

t (Xn+1b)=

b − X

(90)

n+1

n+1 i

Xn+1 (X T Ω−1 X )−1 XnT+1

С учетом (89) формула (90) примет вид:

b − X

)

(91)

t (Xn+1b)= s(X

| X ,

n+1

Итак, t-статистика Стъюдента для X

может быть найдена по формуле (91) и

n+1

t (Xn+1b) t(n − m)

(92)

Следовательно,

P{−tc (ρ,n − m)≤ t (bi )≤ tc (ρ,n − m)}=1−ρ

(93)

Отсюда с учетом (91) и (81):

P{Xn+1b −tcs(Xn+1b | X , Xn+1 )≤ E (Yn+1

| X , Xn+1 )≤ Xn+1b +tcs(Xn+1b | X , Xn+1 )}=1−ρ (94)

Это соотношение определяет интервал для ожидаемого значения E[Yn+1 |

X , Xn+1 ]= Xn+1β :

X ,

(95)

Xn+1b −tcs(Xn+1b |

Xn+1 ), Xn+1b +tcs(Xn+1b | X , Xn+1 ) ,

в который с вероятностью 1−ρ попадает E[Yn+1 | X , Xn+1 ].

Интервальная оценка для Yn+1

Обозначим:

Q =Yn+1 − Xn+1b −ωn+1,1:n P I − X (X T X )−1

X T e

(96)

где (в соответствии с вышеизложенным материалом)

P = Ω

−12

, X = PX

Y = PY ,

, e =Y −Y ,

= Xb .

Несложно показать, что формула (96) может быть также записана в виде:

−Ω

−1

X (X

Ω

−1

X )

−1

(96’)

Q =Yn+1 − Xn+1b −ωn+1,1:n In

Ω

С помощью формулы (96) несложно показать, что

E (Q | X , Xn+1 )= 0

(97)

Покажем независимость необъясненной дисперсии s2 и случайной величины Q :

В силу независимости s2 и b для этого достаточно показать независимость s2 и случайной величины:

Yn+1	−ωn+1,1:n P I −	X (X	T X )−1 X	T e	(98)

	Поскольку	s2	функционально зависит		от вектора e (формула (22)) , для

независимости случайной величины (98) и s2 достаточно показать независимость величины (98) и вектора e , а для этого достаточно показать их некоррелированность (в силу того, что они нормально распределены).

В силу (81):

cov	(	Y	,e \| X	)	= E ε		eT \| X , X		(99)
	(	n+1		)		n+1		n+1
Подставим (21’) и формулу:							ε = Pε в (99), в силу (54) получим:

cov(Yn+1,e \| X )= E{εn+1εT I − X (X T X )−1 X T			\| X , Xn+1}=
= E{εn+1εT P I − X (X T X )−1 X T \| X , Xn+1}= E{εn+1εT \| X , Xn+1}P I − X (X T X )−1 X T =
= σ2ωn+1,1:n P I − X (X T X )−1	X T

Итак,
cov(Yn+1,e \| X , Xn+1 )= σ2ωn+1,1:n P I − X (X T		X )−1 X T					(100)

Из (100), (21’’):
cov{Yn+1 −ωn+1,1:n P I − X (X T X )−1 X T e, e		\| X , Xn+1}=
= cov{Yn+1, e \| X , Xn+1}−ωn+1,1:n P I − X (X		T X )−1 X T var{e		\| X , Xn+1}=
						{σ2	I − X (X T X )−1 X T }=
= σ2ωn+1,1:n P I − X (X T X )−1	X T −ωn+1,1:n P I − X (X T X )−1 X T					{σ2	I − X (X T X )−1 X T }=
= σ2ωn+1,1:n P I − X (X T X )−1	X T −σ2ωn+1,1:n P I − X (X T X )−1				X	T = 0

Итак,
cov{Yn+1 −ωn+1,1:n P I − X (X T X )−1 X T e, e		\| X , Xn+1}= 0					(101)

Отсюда (в соответствии с вышеизложенным) вытекает независимость случайных величин Q

и s2 .

Обозначим через σ(Q | X , Xn+1 ) стандартное отклонение случайной величины (96).

В силу (97) :

Q	\| X , Xn+1 N (0, 1)	(102)
σ(Q \| X , Xn+1 )

Напомним, что

(n − m)

(103)

σ2

В силу независимости Q и s2 случайная величина:

t (Q)=

σ(Q | X , Xn+1 )

(104)

(n − m)

n − m

имеет распределение Стъюдента со степенями свободы

n − m .

Упростив (104), получим:

t (Q)=

(105)

σ(Q | X , Xn+1 )

Найдем σ(Q | X , Xn+1 ).

Подставим (52) в (96):

Q = −Xn+1 (b −β)+ εn+1 −ωn+1,1:n P I − X (X T X )−1

T e

(106)

В силу (106), (89), (14), (54) и с учетом независимости b и e получим:

var(Q | X , Xn+1 )= var(Xn+1b | X , Xn+1 )+ var(εn+1 | X , Xn+1 )+

+var{ω1:n,n+1P I − X (X T X )−1

X T e | X , Xn+1}−

−2cov

2cov

ω1:n,n+1P

I −

−1

e,εn

+1 | X , Xn+1

Xn+1b,εn+1 | X , Xn+1

−

X )

= σ2 Xn+1 (X T Ω−1 X )−1 XnT+1 + σ2ωn+1,n+1 + σ2ωn+1,1:n P I − X (X T X )−1 X T

Pω1:n,n+1 −

−1

−2Xn+1 cov b,εn+1 | X , Xn+1

−

2ωn+1,1:n P I −

X )

cov[e,εn+1 | X , Xn+1 ]

Итак,

var(Q | X , Xn+1 )= σ2 Xn+1 (X T Ω−1 X )−1 XnT+1 + σ2ωn+1,n+1 + σ2ωn+1,1:n P I

− X (X T X )−1 X

T Pω1:n,n+1 −

−1

−2Xn+1 cov b,εn+1 | X , Xn+1

−

2ωn+1,1:n P I −

X )

cov[e,εn+1 | X , Xn+1 ]

(107)

В соответствии с формулой (3.21):

b = β+(X T X )−1 X T ε

(108)

Следовательно, в силу (54) и с учетом формулы ε = Pε получим:

cov b,εn+1 | X , Xn+1 = E (X T X )−1 X T εεn+1 | X , Xn+1 =

= E (X T X )−1 X T Pεεn+1 | X , Xn+1 = (X T X )−1 X T PE[εεn+1 | X , Xn+1 ]=

= σ2 (X T X )−1 X T Pω1:n,n+1

Итак,

−1

Pω1:n,n+1

(109)

cov b,εn+1 |

X , Xn+1 = σ

X )

В силу (54), (21’) и с учетом формулы ε = Pε получим:

cov[e,εn+1 | X , Xn+1 ]= E[eεn+1

| X , Xn+1 ]= E{I − X (X T X )−1

X T Pεεn+1 | X , Xn+1}=

= I − X (X

T X )−1 X T PE{εεn+1 | X , Xn+1}= σ2 I − X (X T X )−1 X

T Pω1:n,n+1

Итак,

cov[e,εn+1 |

X , Xn+1

]= σ2 I − X (X

T X )−1 X T Pω1:n,n+1

(110)

Подставим, (109), (110) в (107):

var(Q | X , Xn+1 )= σ2 {Xn+1 (X T Ω−1 X )−1 XnT+1 + ωn+1,n+1 −

(111)

−ωn+1,1:n P I − X (X T X )−1

X T Pω1:n,n+1

− 2Xn+1 (X T X )−1 X T Pω1:n,n+1}

Подставив формулы: X

= PX ,

P = Ω−12 в (111) получим:

var(Q | X , Xn+1 )= σ2 {Xn+1 (X T Ω−1 X )−1 XnT+1 + ωn+1,n+1 −

(112)

−1

X )

−1

− 2Xn+1

−1

X )

−1

−ωn+1,1:n In

−Ω

Ω

ω1:n,n+1

Ω

ω1:n,n+1}

Обозначим:

z ={Xn+1 (X T Ω−1 X )−1 XnT+1 + ωn+1,n+1 −

(113)

−1

X )

−1

− 2Xn+1

−1

X )

−1

−ωn+1,1:n In

−Ω

Ω

ω1:n,n+1

Ω

ω1:n,n+1}

В силу (113) формулу (112) можно записать в виде:

var(Q | X , Xn+1 )= σ2 z

(114)

Из (114):

σ(Q | X , Xn+1 )= σ

(115)

В силу (114), (115) для var(Q | X , Xn+1 ) и σ(Q | X , Xn+1 ) можно использовать оценки:

		2	z	(116)
var(Q \| X , Xn+1 )= s
s(Q \| X , Xn+1 )= s			(117)
	z
Подставив формулу (115) в (105),				с учетом (117) получим:

t (Q)= ( Q )

s Q | X , Xn+1

Напомним, что t (Q) t(n − m) .

Следовательно,

(118)

(119)

P{−tc (ρ,n − m)≤ t (Q)≤ tc (ρ,n − m)}=1−ρ

(120)

С учетом (79) формула (96’) примет вид:

Q =Yn+1 −

−1

X (X

Ω

−1

X )

−1

Ω

−1

(121)

Yn+1 + ωn+1,1:nΩ

Обозначим:

+ ωn+1,1:nΩ

−1

X (X

Ω

−1

X )

−1

Ω

−1

(122)

Yn+1 =Yn+1

С учетом (122) формулу (121)можно записать в виде:

Q =Y

(123)

−Y

n+1

Из (118), (120), (123) получим:

−t

s(Q | X , X

)≤Y

s(Q | X ,

) =1−ρ (124)

P Y

n+1

≤Y

n+1

{ n+1

n+1

}

Это соотношение определяет прогнозный интервал для Yn+1 :

(125)

Yn+1 −tcs(Q | X , Xn+1 ),

Yn+1 +tcs(Q

| X , Xn+1 ) ,

в который с вероятностью 1−ρ попадает Yn+1 .

В подавляющем большинстве случаев матрица Ω неизвестна.

Однако можно делать предположения о структуре этой матрицы. Например, в случае гетероскедастичности (при отсутствии автокорреляции) матрица Ω диагональна. Такие предположения помагают оценить матрицу Ω.

В случае, когда используется ОМНК с помощью оценки матрицы Ω (поскольку сама матрица Ω не известна), ОМНК называют практически реализуемым (либо доступным) ОМНК.

Реализация ОМНК в случае гетероскедастичности

В этом случае матрица Ω диагональна.

Для оценки диагональных элементов матрицы Ω (т.е. дисперсий случайных отклонений εt ) можно использовать следующую методику.

Вначале используется классическая регрессионная модель: находятся соответствующие коэффициенты b (по формуле b = (X T X )−1 X TY ), прогнозные значения

ˆ			ˆ
Y = Xb и остатки			e =Y −Y (для модели: Y = Xβ+ ε).
Затем строится (классическая) регрессия квадратов полученных остатков e2					на
				t
некоторые переменные Zt = (zt1, , zts ):
e2 = Z		α + υ ,		(126)
t	t		t
где α = (α1, ,αs )			– коэффициенты регрессии (126), υt – случайные отклонения.
В качестве переменных Zt = (zt1, , zts ) могут использоваться переменные Xti , их
квадраты, произведения Xti Xtj , а также другие переменные.
Для коэффициентов α = (α1, ,αs ) строится МНК-оценка:
a = (ZT Z )−1 ZT e2			(127)
и с помощью вектора a строятся оценки для дисперсий случайных отклонений εt :
			(128)
var(εt \| X )= Zt a			(128)
С помощью полученных значений					ˆ
С помощью полученных значений				var(εt \| X ) строится диагональная матрица Ω.
		ˆ	можно использовать вместо матрицы Ω для построения ОМНК-оценок и
Затем матрицу Ω
прогнозов.
Отметим, что при такой методике полагается, что:
var(ε\| X )= Ω				(129)
т.е. что σ2	=1 в гипотезе (3): var(ε\| X )= σ2Ω. Следовательно, в формулах ОМНК можно

считать, что s2 =1.

Другой способ использования ОМНК в условиях гетероскедастичности (при отсутствии автокорреляции) состоит в следующем.

В качестве оценок коэффициентов регрессии используются МНК-оценки: b = (X T X )−1 X TY .

Уайт показал, что матрица:

X )

−1

X )

−1

(130)

var(b | X )= (X

∑et

t =1

является состоятельной

оценкой

матрицы

var(b | X )

ковариаций оценок коэффициентов

регрессии (т.е.

X )

стремиться по вероятности к var(b | X ) при n → ∞ ).

var(b |

Поэтому при

реализации

ОМНК

можно

использовать матрицу

var(b | X )

(построенную по формуле (130)) в качестве оценки

матрицы

var(b | X ). Это

касается

вычисления оценок s(b

| X )

по формуле (40) (и, следовательно,

построения t-статистик и

интервальных оценок для коэффициентов регрессии),

построения F-статистики (формулы

(48’), (50’), (51’)). (В

указанных

формулах следует использовать

вместо

var(b | X )

var(b | X ).)

Реализация ОМНК в случае автокорреляция остатков

Будем

считать,

что

для

модели:

Y = Xβ+ ε

последовательность

случайных

отклонений εt

образует авторегрессионный процесс первого порядка, т.е.

εt = ρεt −1 + υt ,

t =

(131)

1,n

где υt – последовательность независимых нормально распределенных величин с нулевым математическим ожиданием и постоянным стандартным отклонением συ , ρ – коэффициент авторегрессии (причем ρ <1), ε0 – нормально распределенная случайная величина с

нулевым математическим ожиданием и дисперсией σ2 , равной

дисперсии εt постоянны).

Используя равенство (131), несложно показать, что

cov(εt ,εt −k ) = ρk σ2							(132)
	Из	(132)	следует, что ρk				– это коэффициент	корреляции
частности,		ρ – это коэффициент корреляции между εt						и εt −1 ).
	Обозначим:
		ρ	ρ	2	ρ	n−1
	1	ρ	ρ		ρ
Ω =	ρ	1	ρ		ρn−2		(133)
Ω =							(133)
	............................

	ρn−1	ρn−2	ρn−3 1

	σ2	(при которой
	υ
	1−ρ2
	1−ρ2

между εt и εt −k , (в

матрицу состоящую из коэффициентов корреляции между εt при разных значениях t .

(Элемент ωij этой матрицы равен ρi− j .)

В силу (133) ковариационная матрица для вектора ε равна:

var(ε| X )= σ2Ω,

(134)

что согласуется с гипотезой (3).

При известном значении ρ матрица Ω легко находится по формуле (133). Следовательно, для оценки параметров модели: Y = Xβ+ ε, проверки гипотез и построения прогноза можно использовать описанный выше ОМНК.

Однако в подавляющем большинстве случаев значение ρ неизвестно. В этих случаях используется (в частности) процедура Кохрейна-Оркатта (Cochrane-Orcutt). Изложим эту методику.

1)Для исследуемой модели: Y = Xβ+ ε используется МНК и строится вектор остатков e

2)В качестве приближенного значения параметра ρ берется его МНК-оценка r в регрессии: et = ρet −1 + υt

3)С помощью оценки r параметра ρ строится оценка Ωˆ матрицы Ω,

4)С использованием матрицы Ωˆ находятся ОМНК-оценки b , строятся прогнозные

	ˆ	=					ˆ
	значения Y	=	Xb и вектор остатков e			=Y −Y
5)	В качестве нового приближенного значения параметра ρ берется его МНК-оценка r в
	регрессии: e = ρe			+ υ
		t	t −1	t
6)	Процедура повторяется, начиная с шага 3.
	Процесс заканчивается, когда очередное приближение параметра ρ мало отличается от
предыдущего (т.е.			когда величина		rk − rk −1		достаточно мала; здесь индекс k обозначает
предыдущего (т.е.			когда величина		rk − rk −1		достаточно мала; здесь индекс k обозначает
номер итерации).

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Соседние файлы в папке 17-11-2015_11-58-24

#
20.02.201660.42 Кб18Вопросы к экзамену.doc
#
20.02.20161.91 Mб26Задания.rtf
#
20.02.2016534.62 Кб31Методические указания.pdf
#
20.02.20163.81 Mб23Под.ред.Елисеевой.2003.Эконометрика.djvu
#
20.02.201649.66 Кб20Учебная программа.doc
#
20.02.20161.05 Mб57Эконометрика (электронный конспект).pdf