
17-11-2015_11-58-24 / Эконометрика (электронный конспект)
.pdfE[b | X ]= E (X T X )−1 X TY | X = (X T X )−1 X T E[Y | X ]= (X T X )−1 X T Xβ = = (X T X )−1 (X T X )β = Imβ = β
Итак, |
|
E[b | X ]= β. |
(20) |
Следовательно, вектор b является несмещенной оценкой вектора коэффициентов регрессии β.
Можно также показать, что МНК-оценка b является эффективной, т.е. она минимизирует среднеквадратичное отклонение оценки от истинного значения вектора β:
E 
 b −β
b −β
 2 | X , в классе всех несмещенных оценок, линейных по Y .
2 | X , в классе всех несмещенных оценок, линейных по Y .
Найдем ковариационную матрицу для МНК-оценки b .
В силу (18) и (5):
b= (X T X )−1 X TY = (X T X )−1 X T (Xβ+ ε)=
=(X T X )−1 (X T X )β+(X T X )−1 X T ε = β+(X T X )−1 X T ε
Итак, |
|
|
|
|
b = β+(X T X )−1 |
X T ε |
(21) |
|
|
Следовательно, |
|
|
|
|
b −β = (X T X )−1 |
X T ε |
|
(22) |
|
В силу (22) и симметричности матрицы (X T X )−1 : |
|
|||
(b −β)(b −β)T = (X T X )−1 X T εεT X (X T X )−1 |
(23) |
|
||
В силу (23) и (7): |
|
|
|
|
Var[b | X ]= E (b −β)(b −β)T | X = E (X T X )−1 |
X T εεT X (X T X )−1 | X |
= |
||
|
|
|
|
|
= (X T X )−1 X T (σ2 In )X (X T X )−1 = σ2 (X T X )−1 (X T X )(X T X )−1 = σ2 (X T X )−1
Итак, |
|
Var[b | X ]= σ2 (X T X )−1 |
(24) |
Отметим, что формула (24) обобщает формулы (2.24)-(2.26), полученные для парной регрессии.
Отметим, что в силу (24) Var[bi | X ] – это i-й диагональный элемент матрицы (24).
21
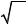
Обозначив элементы матрицы (X T X )−1 через zij , из (24) получим:
Var[bi | X ]= σ2 zii . |
(25) |
||
Обозначим через σ(bi | X ) |
стандартное отклонение коэффициента bi . |
||
В силу (25): |
|
||
σ(bi | X ) = σ |
|
|
(26) |
zii |
|||
Оценка дисперсии ошибок σ2
Как и в случае парной регрессии остатки регрессии et определяются из уравнений:
Y =Yˆ + e |
, |
t = |
|
|
|
|
(27) |
|
||||||||
1,n |
|
|
||||||||||||||
t |
t |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или, в векторном виде: |
|
|
|
|
|
|||||||||||
Y |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
(28) |
|
||
=Y + e |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|||||
e =Y −Yˆ |
, |
t = |
|
|
|
(29) |
|
|||||||||
1,n |
|
|
||||||||||||||
t |
t |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
(30) |
|
||
=Y −Y |
|
|
|
|
|
|
|
|
|
|
|
|
||||
В нашем примере: |
|
|
|
|
|
|
|
|
||||||||
|
|
|
6 |
|
|
|
|
|
6,9077 |
|
-0,9077 |
|||||
|
|
|
12 |
|
|
11,8651 |
|
|
0,1349 |
|
||||||
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
− |
|
9,6095 |
|
= |
|
0,3905 |
|
||||
=Y −Y |
= 10 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
7,0174 |
|
|
|||||||
|
|
|
7 |
|
|
|
|
|
|
|
-0,0174 |
|
||||
|
|
|
|
|
|
|
|
|
2,6003 |
|
|
|
0,3997 |
|
||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||
Из (30):
e =Y −Yˆ = (Xβ+ ε)− Xb = X (β−b)+ ε
Итак,
e = −X (b −β)+ ε
Подставив (21) в (31), получим: e = I − X (X T X )−1 X T ε
(31)
(32)
Докажем, что случайные векторы b и e независимы.
Для их независимости в силу их нормальной распределенности достаточно доказать их некоррелированность.
22
В силу (22), (32), (7):
cov(b,e | X )= E (b −β)eT | X = E (X T X )−1 X T εεT I − X (X T X )−1 X T | X =
=(X T X )−1 X T E εεT | X I − X (X T X )−1 X T =
=σ2 (X T X )−1 X T I − X (X T X )−1 X T = σ2 (X T X )−1 X T −(X T X )−1 X T X (X T X )−1 X T =
=σ2 (X T X )−1 X T −(X T X )−1 X T = 0m×n
где 0m×n – нулевая матрица размера m ×n . |
|
|
|
|
|
|
|
|
|
|
|||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cov(b,e | X )= 0m×n |
|
|
|
|
|
|
|
|
(33) |
|
|
|
|
|
|
||
В силу (33) векторы |
b и e не коррелированны, а следовательно и независимы (в силу их |
||||||||||||||||
нормальной распределенности). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Найдем Var[e | X ]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В силу (32), (7): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| X }= |
|
T |
|
|
|
T |
X ) |
−1 |
X |
T |
|
T |
T |
X ) |
−1 |
X |
T |
|
Var[e | X ]= E ee |
|
| X |
= E{I − X (X |
|
|
|
εε |
I − X (X |
|
|
|
||||||
=σ2 I − X (X T X )−1 X T E εεT | X I − X (X T X )−1 X T =
=σ2 I − X (X T X )−1 X T I − X (X T X )−1 X T = σ2 I − X (X T X )−1 X T
Итак,
Var[e | X ]= σ2 In − X (X T X )−1 |
X T |
(34) |
|
|
|
По аналогии со случаем парной регрессии обозначим:
|
|
|
|
1 |
|
n |
|
|
|
|
1 |
|
|
|
s2 |
= |
|
|
∑et2 |
= |
|
|
eT e (необъясненная дисперсия) |
(35) |
|||||
|
|
|
|
n − m t =1 |
|
|
|
n − m |
|
|
||||
В нашем примере: |
|
|
|
|
||||||||||
|
2 |
|
|
1 |
|
T |
|
|
1 |
|
T |
|
|
|
s |
|
= |
|
e e = |
|
|
e e = 0,5774 |
|
||||||
|
n − m |
5 −3 |
|
|||||||||||
Можно показать, что величина s2 |
является несмещенной оценкой дисперсии ошибок σ2 , |
|||||
т.е. |
|
|
|
|
|
|
|
2 |
|
= σ |
2 |
. |
(36) |
E s |
|
| X |
|
|||
23

Отметим, что в силу формулы (3 5) величина s2 является функцией от вектора e . Следовательно, в силу независимости векторов b и e вектор b и величина s2 также независимы.
|
Можно показать, |
что случайная величина (n − m) |
s2 |
имеет распределение «хи |
||||
|
σ2 |
|||||||
|
|
|
|
|
|
|
|
|
квадрат» с числом степеней свободы n − m : |
|
|
||||||
(n |
− m) |
s2 |
χ |
2 |
(n − m) |
(37) |
|
|
σ2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Напомним, что распределение «хи квадрат» с n степенями свободы – это распре- |
|||||||
деление следующей случайной величины: |
|
|
||||||
|
|
n |
|
|
|
|
|
|
χ2 |
(n) = ∑εk2 |
|
|
(38) |
|
|
||
k =1
где ε1, ,εn – независимые стандартные нормальные случайные величины.
Квадратный корень из s2 называется стандартной ошибкой оценки (стандартной ошибкой регрессии).
В нашем примере: s = 
 s2 = 0,7598
s2 = 0,7598
Обозначим:
|
2 |
(X |
T |
X ) |
−1 |
, |
(39) |
Var[b | X ]= s |
|
|
|
Всилу несмещенности оценки s2 из (24) следует, что матрица (39) является несмещенной оценкой ковариационной матрицы векторной МНК-оценки b .
Внашем примере:
|
|
|
|
|
|
|
|
3,8617 |
-0,0726 -0,0167 |
||
|
2 |
(X |
T |
X ) |
−1 |
|
0,0016 |
0,0002 |
|
||
Var[b | X ]= s |
|
|
|
|
= -0,0726 |
|
|||||
|
|
|
|
|
|
|
|
|
0,0002 |
0,0002 |
|
|
|
|
|
|
|
|
|
-0,0167 |
|
||
В силу (25) величина |
|
|
|
|
|
||||||
|
|
2 |
zii |
|
|
|
|
(40) |
|
|
|
Var[bi | X ]= s |
|
|
|
|
|
|
|
|
|||
является несмещенной оценкой дисперсии МНК-оценки bi . Обозначим:
|
(41) |
s(bi | X ) = Var[bi | X ] |
24
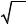
оценку стандартного отклонения bi . В нашем примере:
i |
|
|
| X ] |
s(b | X ) |
|
||
|
|
Var[bi |
i |
|
|||
1 |
|
3,8617 |
|
1,9651 |
|
||
|
|
|
|
|
|
|
|
2 |
|
0,0016 |
|
0,0397 |
|
||
|
|
|
|
|
|
|
|
3 |
|
0,0002 |
|
0,0145 |
|
||
|
|
|
|
|
|
||
Отметим, что из (40), (41): |
|||||||
s(bi | X ) = s |
|
|
|
|
(41’) |
||
|
zii |
|
|||||
25

Пусть |
t – (условно) нормально распределенные случайные величины. Следовательно, |
||||||||||
| X |
2 |
In , |
|
|
|
|
(42) |
||||
N 0, |
|
|
|
|
|
||||||
где In |
– единичная матрица размером |
n n . |
|||||||||
Тогда и Yt (условно) |
нормально распределенные величины, а следовательно и векторная |
||||||||||
МНК-оценка |
|
|
b |
|
также условно нормально распределена (поскольку она линейна |
||||||
относительно |
|
Y ). |
|
|
|
|
|
|
|||
В силу (20) и (24) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
b | X |
|
2 |
|
X |
T |
X |
|
1 |
(43) |
||
N , |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что
b |
|
|
||
i |
|
i |
| X |
|
(b |
| X ) |
|||
|
||||
|
i |
|
|
|
b |
|
i |
|
|
|
i |
|
стандартная нормальная случайная величина, т.е. |
|||
(b | X ) |
|||||
|
|
||||
|
i |
|
|
|
|
|
N 0, |
1 |
(44) |
||
Как было указано выше, случайная величина (n m) |
s2 |
имеет распределение «хи квадрат» с |
|
2 |
|||
|
|
числом степеней свободы n m :
|
s |
2 |
|
|
|
|
|
|
|
|
(n m) |
|
2 |
(n m) |
|
|
|
(44’) |
|||
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
Кроме того, выше мы доказали, что вектор b |
и величина s |
2 |
||||||||
|
||||||||||
|
|
|
|
|
b |
i |
|
и (n m) |
s2 |
|
Следовательно, случайные величины |
i |
|
|
|
||||||
(b | X ) |
2 |
|
||||||||
|
|
|
|
|
i |
|
|
|
|
|
Поэтому с учетом (44) и (44’) случайная величина:
независимы.
также независимы.
|
|
|
|
bi i |
|
|
|
|
|
|
|
|||
t bi |
|
|
|
(bi | X ) |
|
|
|
|
(44’’) |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
s2 |
|
|
|||||
|
|
|
1 |
|
m) |
|
|
|||||||
|
|
|
|
|
(n |
|
|
|
|
|||||
|
|
|
|
|
|
2 |
|
|||||||
|
|
|
n m |
|
|
|
|
|
||||||
имеет распределение Стъюдента со степенями свободы |
n m . |
|||||||||||||
|
Упростив (44’’), получим: |
|
||||||||||||
t bi |
|
|
bi i |
|
|
|
|
|
(45) |
|
||||
|
s |
(bi |
| X ) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
Напомним, |
что |
|
распределение Стъюдента |
с n степенями свободы – это |
|||||||||
распределение следующей случайной величины: |
|
|||||||||||||
26

t(n) |
|
|
0 |
|
, |
(45’) |
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|||
|
|
2 |
(n) |
|
|
|
|||
|
|
|
|
|
|||||
|
n |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
где 0 |
и |
|
2 |
(n) |
– независимые стандартная нормальная случайная величина и случайная |
||||
|
|||||||||
величина, имеющая распределение «хи квадрат» с |
n |
степенями свободы. |
|||||||
|
Подставим (26) в формулу (45) примет вид: |
|
|
||||||
t b |
b |
||
i |
i |
||
|
|||
i |
s |
z |
|
|
|||
|
|
ii |
|
(45’’)
В силу (41’) формулу (45’’) запишем в виде:
t b |
b |
||
i |
i |
||
|
|||
i |
s(b |
| X ) |
|
|
|||
|
i |
|
|
(46)
|
Напомним, |
что |
случайная |
величина |
t bi |
имеет распределение |
Стъюдента со |
степенями свободы |
n m : |
|
|
|
|
||
t bi |
t(n m) |
|
(47) |
|
|
|
|
Статистики t bi , |
как |
и в случае |
парной регрессии, можно использовать |
для проверки |
|||
гипотез и для построения доверительных интервалов. (см. тему 2). Отметим, что методика проверки гипотез и построения доверительных интервалов основана на использовании соотношения:
P t , n m t bi t ,n m 1 , |
(48) |
где |
t , n m |
двусторонняя квантиль распределения Стъюдента с числом степеней свободы |
n m при уровне значимости . |
|
|
Пусть 0,05 . |
|
|
В условиях нашего примера n 5 , m 3 |
и |
t , n m 4,3027 . |
Найдем t-статистики коэффициентов регрессии при i |
0 |
по формуле (46): |
i
1
2
3
bi
3,8617
0,0016
0,0002
s(b |
| X ) |
i |
|
1,9651
0,0397
0,0145
t b |
|
i |
|
-0,2786
6,6315
-3,9868
Как видно из таблицы, значимым коэффициентом является только 2 .
27

Как и в случае парной регрессии доверительные интервалы для коэффициентов |
i |
имеют |
|||||||
вид: |
|
|
|
|
|
|
|
|
|
bi |
t , n m s(bi |
| X ), |
bi t , n m s(bi |
| X ) |
(49) |
|
|
||
|
|
|
|
|
|
|
|
|
|
В нашем случае: |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
i |
95%-й доверительный |
|
|
|
|
||||
|
интервал для |
i |
|
|
|
|
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 |
|
-9,0028; |
|
|
|
|
|
|
|
|
|
7,9078 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
0,0925; |
|
|
|
||
|
|
0,4344 |
|
|
|
||
|
|
|
|
|
|
||
3 |
-0,1199; |
0,0046 |
|
|
|||
|
|
|
|
|
|
2 |
|
Проверка общего качества уравнения регрессии. Коэффициент детерминации |
R |
||||||
|
|||||||
Напомним:
|
n |
|
t |
TSS |
|
|
|
|
Y |
||
|
t 1 |
|
|
|
|
t |
|
|
n |
|
|
ESS |
|
|
Y |
|
i 1 |
|
|
Y 2
ˆ 2
Yi
,
,
(total sum of squares, полная сумма квадратов), |
(50) |
(error sum of squares, остаточная сумма квадратов) |
(51) |
|
|
t |
|
|
|
|
n |
ˆ |
|
|
2 |
RSS |
|
Y |
|
||
|
Y |
|
|
t1
Внашем случае:
, (regression sum of squares, объясненная сумма квадратов)
(52)
|
n |
t |
|
|
|
|
|
||
TSS |
|
Y Y |
2 |
49,2 |
|
|
|||
|
t 1 |
|
|
|
|
|
|
|
t |
|
|
|
i |
|
|
|
||
|
|
|
n |
|
|
|
|
|
ˆ |
2 |
|
|
|
ESS |
|
|
|
|
|
|
1,1547 |
|
|||||
|
|
Y Y |
|
|
|||||||||
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
ˆ |
Y |
|
48,0453 |
|
||||
RSS Yt |
|
|
|||||||||||
|
|
|
t 1 |
|
|
|
|
|
|
|
|
|
|
Обозначим: |
|
|
|
|
|
|
|
|
|||||
R |
2 |
1 |
|
ESS |
|
RSS |
(53) |
||||||
|
|
|
|
|
|
||||||||
|
TSS |
TSS |
|||||||||||
|
|
|
|
|
|
|
|
||||||
Статистику |
R |
2 |
называют коэффициентом детерминации. |
||||||||||
|
|
||||||||||||
В нашем случае:
R2 0,9765
Чем больше значение R2 к 1, тем лучше качество подгонки.
28

Проверка гипотезы: H H – матрица размером
r q m
,
q
m
,
rank(H )
q
,
r |
– вектор-столбец длиной |
Пусть, например:
q
.
1 |
0 |
H |
|
|
1 |
0 |
0 -1
,
r
|
2 |
|
|
|
|
0 |
|
|
,
q 2
Тогда гипотезу H r можно записать в виде системы двух равенств:
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
E Hb r | |
X H r |
|
|
|
|
|
|
(54) |
|
|
|
|
|
|
|
|
||||
Var Hb r | X E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Hb r H r Hb r H |
r |
T |
| X |
|
|
|||||||||||||||
|
|
|||||||||||||||||||
E |
H b H b |
|
| |
X |
|
E H b b |
H |
|
| X |
|
|
|||||||||
|
|
|
|
|
|
|
T |
|
|
|
|
|
T |
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
H E b b |
| X H |
|
H Var b | X H |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
T |
|
|
|
T |
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Var Hb r | X H Var b | |
X H |
T |
(55) |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
Подставим (24) в (55): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Var Hb r | X 2 H X T X 1 H T |
|
(56) |
|
|
|
|
|
|
|
|||||||||||
Итак,
|
|
2 |
T |
|
|
|
T |
Hb r | X |
N H r, H X |
|
X |
1 |
H |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Можно показать, что при выполнении гипотезы:
H r |
(58) |
величина:
(57)
|
|
T |
|
|
1 |
|
T |
1 |
|
T |
H X |
|
X |
|
|
|
Hb r |
||
Hb r |
|
|
H |
|
|
||||
F |
|
|
|
|
|
|
|
|
(59) |
|
|
2 |
q |
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
s |
|
|
|
|
|
||
имеет распределение Фишера (F-распределение) с (q, n m) степенями свободы:
F F(q,n m) |
(60) |
Напомним, что распределение Фишера с (q, n m) степенями свободы – это распределение следующей случайной величины:
29

|
|
1 |
|
2 |
(q) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F (q, n) |
|
|
|
|
|
|
|
|
|
|
|
|
(61) |
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
(n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
(q) |
и |
2 |
(n) |
|
– |
независимые случайные величины, имеющие |
распределения |
«хи |
|||||||||
где |
|
|
||||||||||||||||
квадрат» с |
q |
|
и n степенями свободы, соответственно. |
|
|
|
||||||||||||
Следовательно, при выполнении гипотезы (58) имеет место равенство: |
|
|
|
|||||||||||||||
P F Fc ;q,n m 1 , |
|
|
(62) |
|
|
|
||||||||||||
где Fc ;q, n m |
– |
(1 ) -квантиль распределения Фишера с (q, n m) степенями свободы. |
||||||||||||||||
В случае, если F Fc ;q, n m нулевая гипотеза отвергается; если |
F Fc ;q, n m |
, нет |
||||||||||||||||
оснований отвергать нулевую гипотезу (и она принимается). |
|
|
|
|||||||||||||||
В условиях нашего примера при указанных выше H , r и q при 0,05 |
: |
|
||||||||||||||||
F ;q, n m 39 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
1 |
|
T |
|
1 |
|
|
|
|
|
|
|
T |
H X |
|
X |
|
|
|
|
Hb r |
|
|
|
||||
Hb r |
|
|
|
H |
|
|
|
|
|
|
||||||||
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
64,7002 |
|
|
|
|
|
|
|
|
|
|
2 |
q |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
||
Следовательно, в данном случае нулевая гипотеза:
1
2
,
|
2 |
|
0 |
|
3 |
|
отвергается.
В частном случае, когда нулевая гипотеза имеет вид:
2 |
3 |
|
|
m 0 |
, |
(63) |
||||||
для модели: |
|
|
|
|
|
|||||||
|
|
|
m |
X |
|
|
|
|
|
|||
Y |
|
|
ti |
t |
|
|
||||||
t |
1 |
|
|
i |
|
|
|
|||||
|
|
|
|
|
i 2 |
|
|
|
|
|
||
формулу (59) можно привести к виду: |
|
|||||||||||
|
|
R |
2 |
|
|
n m |
|
|
|
|
||
F |
|
|
|
|
|
|
(64) |
|||||
R |
2 |
m |
1 |
|
|
|
||||||
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
В условиях нашего примера:
R2 1 TSSESS 1 49,20001,1547 0,9765
F |
|
R2 |
|
n m |
|
0,9765 5 3 |
41,6075 |
|||
|
|
|
|
|
|
|
|
|||
|
R2 |
|
m 1 |
1-0,9765 3 1 |
||||||
1 |
|
|
|
|||||||
Fc ;m 1, n m 39 .
Следовательно, нулевая гипотеза: 2 3 0 отвергается
30
