17-11-2015_11-58-24 / Эконометрика (электронный конспект)

i=1

Модель (14) – это так называемая двойная логарифмическая модель (и зависимая, и объясняющие переменные заданы в логарифмическом виде).

увеличении X в расчете на одну единицу.)

Эту модель целесообразно использовать, если есть основания считать, что при равных

41

фактора Xi в расчете на 1%.

Эту модель целесообразно использовать, если есть основания считать, что при равных

i=1

где Xti = ln Xti .

Отметим, что любая модель вида:

42

либо

i=1

Качественные переменные Например, при исследовании зависимости зарплаты от различных факторов может

возникнуть вопрос, влияет ли на ее размер, и если да, то в какой степени, наличие у работника высшего образования.

Введем переменную dt , описывающую наличие у работника высшего образования Положим:

Переменная dt описывает качественный признак, а не количественное значение. Такие переменные называются качественными.

Обычно качественные переменные принимают только два значения: 0 и 1. Принято считать, что качественная переменная равна 1 в случая наличия признака, и 0 – в случае его отсутствия. Такие переменные также называются бинарными, двоичными, логическими. В англоязычной эконометрической литературе их называют “dummy variables”, что на русский язык часто переводится как “фиктивные переменные.”

Пусть модель имеет вид:

i=1

где yt размер зарплаты работника, xti – влияющие на нее факторы, dt – качественная переменная, описывающая наличие у работника высшего образования, δ – коэффициент регрессии.

Методика работы с моделью вида (31) такая же, как и для любой линейной регрессионной модели. Экономический смысл коэффициента регрессии δ состоит в том, что этот коэффициент показывает насколько заработная плата работника с высшим образованием в среднем отличается от заработной платы работника без высшего образования с такими же значениями других объясняющих факторов.

Если включаемый в рассмотрение качественный признак имеет не два, а несколько значений, используют несколько бинарных переменных. Типичным примером подобной ситуации является исследование сезонных колебаний. Пусть, например, yt – объем потребления некоторого продукта в месяц t , и есть основания считать, что потребление

43

зависит от времени года. Для выявления влияния сезонности можно ввести четыре бинарные

объеме потребления зимних, весенних и летних месяцев по отношению к осенним месяцам. Отметим, что ввиду присутствия в (36) свободного члена мы не вводим в (36)

четвертую бинарную переменную d4 , относящуюся к осени, иначе тогда для любого месяца t выполнялось бы тождество dt1 + dt 2 + dt3 + dt 4 =1, что означало бы линейную зависимость регрессоров в (36), и как следствие, невозможность получения МНК-оценок. (Напомним, что матрица X T X должна быть не вырождена.)

Ситуация, когда при наличии в уравнении регрессии свободного члена сумма фиктивных переменных равна константе, называется “dummy trap”. При построении уравнения регрессии с качественными переменными следует обращать внимание на возможность такой ситуации.

Фиктивные переменные позволяют строить и оценивать так называемые кусочнолинейные модели, которые можно применять для исследования структурных изменений.

Пусть, например, xt –размер основного фонда в период t , yt – объем продукции, выпущенной в этот же период. Из некоторых априорных соображений исследователь

44

считает, что в момент t0 произошла структурная перестройка и линия регрессии будет отличаться от той, что была до момента t0 , но общая линия остается непрерывной.

Чтобы оценить такую модель, введем бинарную переменную r , полагая, что

Регрессионная линия, соответствующая (38), имеет коэффициент наклона β2 для t ≤ t0 и

произошло.

45

5. Мультиколлинеарность, гетероскедастичность и автокорреляция остатков

Мультиколлинеарность Одним из условий классической линейной регрессионной модели является предполо-

жение о линейной независимости объясняющих переменных, что означает линейную независимость столбцов матрицы X или (эквивалентно), что матрица X T X не вырождена. При нарушении этого условия, т.е. когда один из столбцов матрицы X есть линейная комбинация остальных столбцов, говорят, что имеет место полная коллинеарность. В этой ситуации нельзя построить МНК-оценку вектора параметров β, поскольку b = (X T X )−1 X TY .

На практике полная коллинеарность встречается исключительно редко. Гораздо чаще приходится сталкиваться с ситуацией, когда матрица X имеет полный ранг, но между регрессорами имеется высокая степень корреляции, что приводит к тому, что матрица X T X близка к вырожденной. Тогда говорят о наличии мультиколлинеарности. В этом случае МНК-оценка существует, но обладает «плохими» свойствами.

Мультиколлинеарность может возникнуть в силу разных причин. Например, несколько независимых переменных могут иметь общий временной тренд, относительно которого они совершают малые колебания.

Признаки мультиколлинеарности:

1)Небольшое изменение исходных данных (например, добавление новых наблюдений) приводит к существенному изменению оценок bi коэффициентов регрессии.

2)Оценки bi имеют большие стандартные ошибки s(bi | X ) (и, следовательно, большие доверительные интервалы), малую значимость (т.е. малые t-статистики

3)Оценки коэффициентов bi имеют неоправданные с точки зрения теории знаки или неоправданно большие значения.

4)Парная корреляция между малозначимыми объясняющими переменными достаточно высока.

5)Высокие частные коэффициенты корреляции.

46

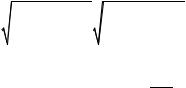
Напомним, что выборочный коэффициент (парной) корреляции между переменными xi и xj находится по формуле:

Выборочный частный коэффициент корреляции находится следующим образом. Пусть даны переменные xi , i =1,m .

Обозначим I ={1,2, ,m}.

Таким образом, коэффициент частной корреляции позволяет исключить влияние других факторов на взаимосвязь между рассматриваемыми переменными.

Последствия мультиколлинеарности

1)Большие стандартные ошибки затрудняют нахождение истинных значений определяемых величин и расширяют их интервальные оценки, ухудшая их точность.

2)Ухудшается качество прогноза.

47

3)Малые t-статистики коэффициентов могут привести к неоправданному выводу о их малой значимости, т.е. о слабом влиянии соответствующей объясняющей переменной на зависимую переменную.

4)Оценки коэффициентов и их стандартные ошибки становятся очень чувствительными к малейшим изменениям данных, т.е. они становятся неустойчивыми.

Методы устранения мультиколлинеарности

1)Исключение переменных из модели. Исключается из модели одна или несколько коррелированных объясняющих переменных. Например, можно последовательно исключать из модели объясняющие переменные с наименьшими незначащими t- статистиками коэффициентов регрессии (причем после каждого исключения из модели объясняющей переменной следует производить пересчет t-статистик для оставшихся объясняющих переменных).

2)Можно использовать описанный в предыдущей теме алгоритм оптимального отбора объясняющих переменных, основанный на использовании скорректированного коэффициента детерминации Ra2 .

3)Получение дополнительных данных или новой выборки

4)Изменение спецификации модели

5)Преобразование переменных.

Гетероскедастичность и автокорреляция остатков

Гетероскедастичность означает, что дисперсии var(εt | X ) случайных отклонений εt зависят от t , т.е. нарушается гипотеза классической модели о постоянстве этих дисперсий. Автокорреляция остатков означает, что ковариации cov(εt ,εs | X ) не равны нулю при разных значениях t и s .

Суть и причины гетероскедастичности

Гетероскедастичность означает, что var(εt | X ) зависит от номера наблюдения t . Обычно эта зависимость возникает вследствие зависимости εt от Xt . Например, если Xt – уровень до-

хода семьи, а Yt – ее потребление, естественно ожидать что для семей с высоким доходом разброс в их потреблении больше, чем для семей с низким доходом.

48

Проблема гетероскедастичности характерна для перекрестных данных и довольно редко встречается при рассмотрении временных рядов.

Последствия гетероскедастичности

1)Оценки коэффициентов регрессии, оставаясь линейными и несмещенными, перестают быть эффективными, что (в частности) ухудшает прогноз.

2)Дисперсии и ковариации оценок являются смещенными. Это приводит к искажению значений статистик Стъюдента и Фишера, что негативным образом сказывается на результаты проверки гипотез и построении интервальных оценок.

Обнаружение гетероскедастичности Графический анализ остатков.

По оси абсцисс откладываются либо номера наблюдений t , либо значения объясняющей переменной xti , либо линейная комбинация объясняющих переменных, либо прогноз-

ные значения yˆt объясняемой переменной. По оси ординат – либо отклонения et , либо их

Тест Уайта (White)

Сначала к исходной модели применяется обычный метод наименьших квадратов и находятся остатки регрессии et , t =1,n . Затем осуществляется регрессия квадратов этих остатков et2 на все регрессоры xti исходной модели, их квадраты xti2 , попарные произведения xti xtj и константу (если ее не было в составе исходных регрессоров). Для этой регрессии

находится коэффициент детерминации R2 . Тогда при выполнении нулевой гипотезы о постоянстве дисперсий случайных отклонений величина:

асимптотически (т.е. при большом количестве наблюдений n ) имеет распределение χ2 (N −1) , где N – число регрессоров второй регрессии.

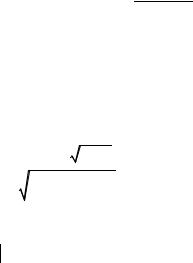
Напомним, что распределение «хи квадрат» с n степенями свободы – это распределение следующей случайной величины:

k =1

где ε1, ,εn – независимые стандартные нормальные случайные величины.

49

Следовательно, при выполнении нулевой гипотезы имеет место равенство:

лать вывод о наличии гетероскедастичности); если χ2 ≤ χc2 (ρ, N −1), нет оснований отвергать нулевую гипотезу (и, она принимается).

Тест ранговой корреляции Спирмана Этот тест применяется, когда есть предположение о прямой зависимости дисперсии

ошибки от величины некоторой независимой переменной. Значения такой независимой переменной xti и абсолютные величины отклонений et ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:

n

∑dt2

r (xi ,e)=1−6 (t =1 ), (11) n n2 −1

где di – разность между рангами xti и et . (Например, если при t = 20 значение x20,i является 25-м по величине среди всех наблюдений xti , а e20 является 32-м, то d20 = 25 −32 = −7 .)

имеет распределение Стъюдента с числом степеней свободы n − 2 . Следовательно, если

(где tc (ρ,n − 2) двусторонняя квантиль распределения Стъюдента с n − 2 степенями свобо-

ды при уровне значимости ρ), то нулевая гипотеза о равенстве нулю коэффициента корреля-

ции ρ(xti ,εt ) отклоняется, и, следовательно, можно сделать вывод о присутствии гетеро-

скедастичности.

Тест Голфельда-Куандта (Goldfeld-Quandt)

Этот тест также применяется, когда есть предположение о прямой зависимости дисперсии ошибки от величины некоторой независимой переменной.

Нужно:

50