Задачи для самостоятельного решения

10.1.Дискретная случайная величинаХзадана законом распределения

Х	1	3	5
Р	0,4	0,1	0,5

Найти закон распределения случайной величины .

Ответ:

Y	3	9	15
Р	0,4	0,1	0,5

10.2.Дискретная случайная величинаХзадана законом распределения

Х	3	6	10
Р	0,2	0,1	0,7

Найти закон распределения случайной величины .

Ответ:

Y	7	13	21
Р	0,2	0,1	0,7

10.3.Дискретная случайная величинаХзадана законом распределения

Х	–1	–2	–1	2
Р	0,3	0,1	0,2	0,4

Найти закон распределения случайной величины .

Ответ:

Y	1	4
Р	0,5	0,5

10.4.Дискретная случайная величинаХзадана законом распределения

Х
Р	0,2	0,7	0,1

Найти закон распределения случайной величины .

Ответ:

Y		1
Р	0,3	0,7

10.5.Задана плотность распределенияслучайной величиныХ, возможные значения которой заключены в интервале. Найти плотность распределенияслучайной величины, если а)б)в)г); д)

Ответ: а),б),;

в) ,; г),;

д) ,.

10.6.Задана плотность распределенияслучайной величиныХ, возможные значения которой заключены в интервале. Найти плотность распределенияслучайной величиныесли а)б)в)г)д)

Ответ:а),;

б) ,;

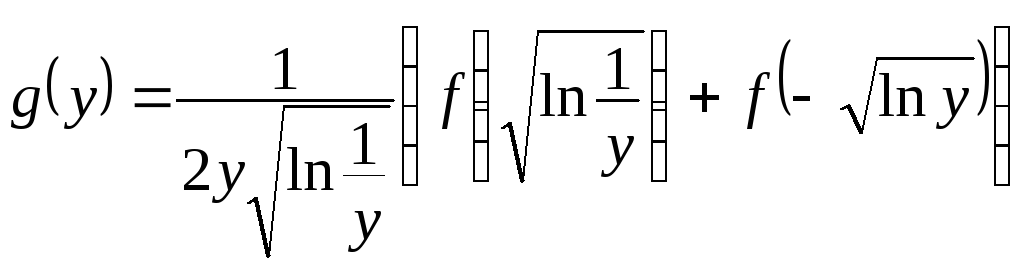в) ,;

г) ,;

д) ,

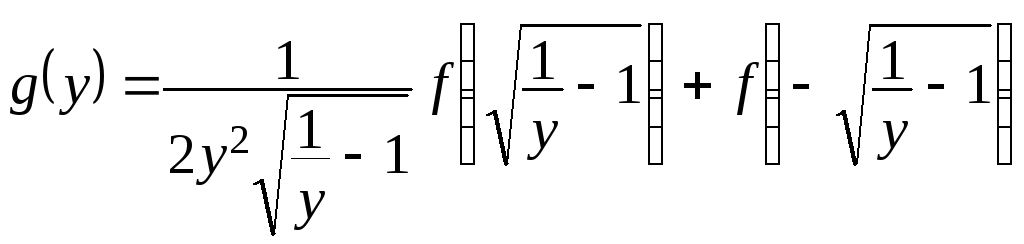10.7.Задана плотность распределениянормально распределенной случайной величиныХ. Найти плотность распределения случайной величины.

Ответ:в интервале; вне этого интервала.

10.8.Задана функция распределенияслучайной величиныХ. Найти функцию распределенияслучайной величины

Ответ:

10.9.Задана функция распределенияслучайной величиныХ. Найти функцию распределенияслучайной величины.

Ответ: .

10.10.Задана функция распределенияслучайной величиныХ. Найти функцию распределенияслучайной величиныесли а)б)в)

Ответ: а) ; б);

в) при,при.

Функция двух случайных аргументов

Если каждой паре возможных случайных величин Хисоответствует одно возможное значение случайной величинытоназывают функцией двух случайных аргументовХии пишут

.

Если Хидискретные независимые случайные величины, то для нахождения распределения функции, надо найти все возможные значе­ния, для чего достаточно для каждого возможного значенияХ, равного, и каждого возможного значенияравного, вычислить значениеравное. Вероятности найденных возможных значенийравны произведениям вероятностейи.

Пример 10.6.Дискретные независимые случайные величиныХизаданы распределениями:

Х	–2	–1	3	4
Р	0,3	0,1	0,5	0,1

Y	1	2	3
Р	0,4	0,1	0,5

Найти распределения случайных величин: а) б)в)г)

Решение.Для того чтобы составить указанные распределения величинынадо найти все возможные значенияи их вероятности. Все вычисления поместим в таблицу

Х					2
–2	1	–1	–5	–2	–2	0,3 · 0,4 = 0,12
–2	2	0	–6	–4	–8	0,3 · 0,1 = 0,03
–2	3	1	–7	–6	–18	0,3 · 0,5 = 0,15
–1	1	0	–3	–1	–1	0,1 · 0,4 = 0,04
–1	2	1	–4	–2	–4	0,1 · 0,1 = 0,01
–1	3	2	–5	–3	–9	0,1 · 0,5 = 0,05
3	1	4	5	3	3	0,5 · 0,4 = 0,20
3	2	5	4	6	12	0,5 · 0,1 = 0,05
3	3	6	3	9	27	0,5 · 0,5 = 0,25
4	1	5	7	4	4	0,1 · 0,4 = 0,04
4	2	6	6	8	16	0,1 · 0,1 = 0,01
4	3	7	5	12	36	0,1 · 0,5 = 0,05
						1,00

Объединив одинаковые значения и расположив их в порядке возрастания, получим следующие распределения:

а)

	–1	0	1	2	4	5	6	7
	0,12	0,07	0,16	0,05	0,20	0,09	0,26	0,05

б)

	–7	–6	–5	–4	–3	3	4	5	6	7
	0,15	0,03	0,17	0,01	0,04	0,25	0,05	0,25	0,01	0,04

в)

	–6	–4	–3	–2	–1	3	4	6	8	9	12
	0,15	0,03	0,05	0,13	0,04	0,20	0,04	0,05	0,01	0,25	0,05

г)

	–18	–9	–8	–4	–2	–1	3	4	12	16	27	36
	0,15	0,05	0,03	0,01	0,12	0,04	0,2	0,04	0,05	0,01	0,25	0,05

Если Хинепрерывные независимые случайные величины, то плотность распределениясуммы(при условии, что плотность распределения хотя бы одного из аргументов задана в интервалеодной формулой) может быть найдена по формуле

либо по равносильной формуле

где и— плотности распределения аргументов.

Если возможные значения аргументов неотрицательны, то плотность распределения величинынаходят по формуле

либо по равносильной формуле

В том случае, когда обе плотности изаданы на конечных интервалах, для отыскания плотностивеличиныцелесообразно сначала найти функцию распределения, а затем продифференцировать ее по

.

Если Хи— независимые случайные величины, заданные соответству­ющими плотностями распределенияи, то вероятность попадания случайной точкив областьравна двойному интегралу по этой области от произведения плотностей распределения

Пример 10.7. Независимые нормально распределенные случайные величины Х и заданы плотностями распределений,. Найти композицию этих законов, т.е. плотность распределения случайной величины

Решение.Используем формулуТогда

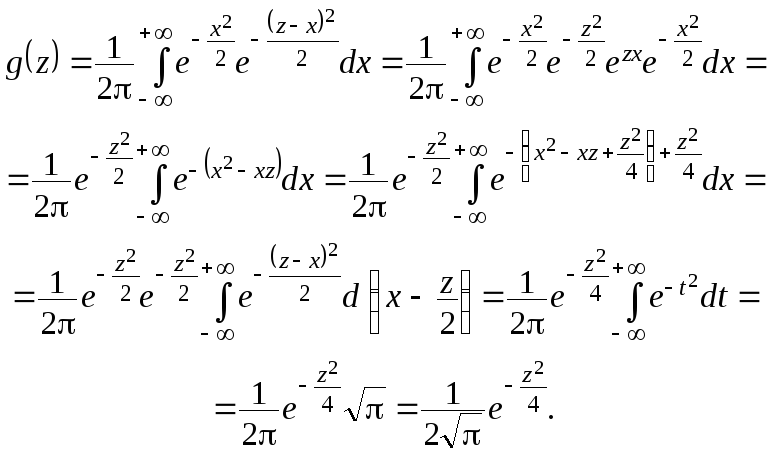
Ответ:.

Пример 10.8.Заданы плотности распределения независимых равномерно распределенных случайных величинХив интервале (0; 2), вне этого интервала,в интервале (0; 3), вне этого интервала. Найти функцию распределения и плотность распределения случайной величиныПостроить график распределения.

Р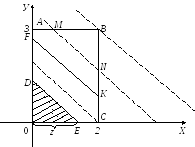ешение.По условию, возможные значенияХопределяются неравенством,— неравенством. Отсюда следует, что возможные случайные точкирасположены в прямоугольникеОАВС (рис. 10.1).

Рис. 10.1

Неравенствуудовлетворяют те точкиплоскостикоторые лежат ниже прямойесли же брать только возможные значенияхиу, то неравенствовыполняется только для точек, лежащих в прямоугольникеОАВСниже прямойС другой стороны, так как величиныХинезависимы, то

где — величина той части площади прямоугольникаОАВС, которая лежит ниже прямойВеличина этой площади зависит от значения

Если тот.е.

Если , то

Если , то

.

Если , то

Если , то

Итак, искомая функция распределения имеет вид

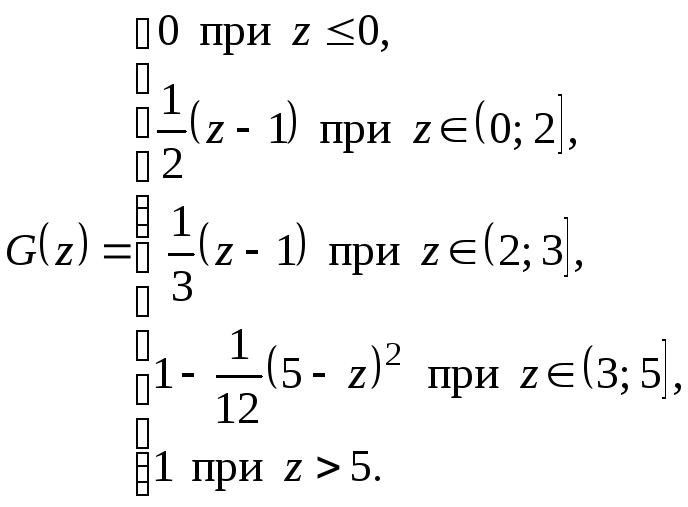
Найдем плотность распределения

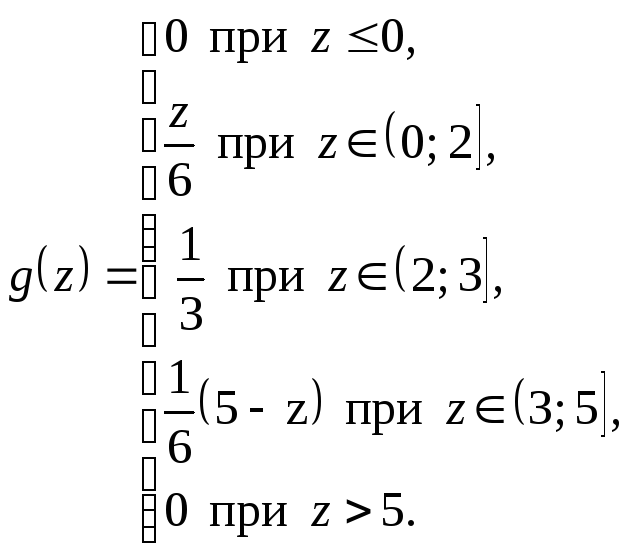
Построим график этой функции (рис. 10.2)

Рис. 10.2