6. Повторные независимые испытания (схема Бернулли)

Ряд классических распределений связан с экспериментом, в котором проводятся последовательные независимые испытания и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.

Последовательные испытания называются независимыми, если вероятность осуществления любого исхода вn-м по счету испытании не зависит от реализации исходов предыдущих испытаний.

Простейшим классом повторных независимых испытаний является последовательность независимых испытаний с двумя исходами(«успех» и «неуспех») и с неизменными вероятностями «успеха» (р) и «неуспеха» в каждом испытании (схема испытаний Бернулли).

Вероятность получить ровно mуспехов вnнезависимых испытаниях вычисляется по формуле, называемойформулой Бернулли

.

Пример 6.1.Изделия некоторого производства содержат 5 % брака. Найти вероятность того, что среди пяти взятых наугад изделий: а) нет ни одного испорченного; б) будут два испорченных.

Решение. а) По условию задачи . Так как вероятность наступ­ления событияА(появление бракованной детали) постоянна для каждого испытания, то задача подходит под схему Бернулли. Находим вероятность того, что среди пяти взятых наудачу изделий нет ни одного испорченного. По формуле Бернулли

а) ;

б) ,

.

Ответ:а); б).

Определение.Число наступлений событияАназываетсянаивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления событияА любое другое количество раз.

Наивероятнейшее число наступлений события Авnиспытаниях заключено между числамии:. Если— целое число, то наивероятнейших чисел дваи.

Пример 6.2.В помещении четыре лампы. Вероятность работы в течение года для каждой лампы 0,8. Чему равно наивероятнейшее число ламп, которые будут работать в течение года?

Решение. По формуленайдемПо условию

.

Следовательно, имеются два наивероятнейших числа или.

Ответ:или.

Пример 6.3.Вероятность попадания в кольцо при штрафном броске для баскетболиста равна 0,8. Сколько надо произвести бросков, чтобы наивероятнейшее число попаданий было равно 20?

Решение. Известно, что. Тогдаиnнайдем из системы неравенств

Так как n— целое число, тоили.

Ответ:24 или 25.

Задачи для самостоятельного решения

1. Наблюдениями установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность того, что из случайно взятых в этом месяце 8 дней 3 дня окажутся дождливыми?

Ответ:

6.2.Что вероятнее: выиграть у равносильного противника (ничейный исход партии исключен) три партии из четырех или пять из восьми?

Ответ:

6.3.В банк поступило 6 заявлений от физических лиц на получение кредита. Вероятность получить первый кредит для каждого равна . Найти вероятности следующих событий:

1) будет выдано ровно 3 кредита;

2) будет выдано не менее двух кредитов.

Ответ:.

4. Вероятность рождения мальчика равна 0,515, девочки 0,485. В некоторой семье шестеро детей. Найти вероятность того, что среди них не больше двух девочек.

Ответ:;.

6.5. Два баскетболиста делают по три броска в корзину. Вероятность попадания мяча при каждом броске равна соответственно 0,6 и 0,7. Найти вероятность того, что у обоих будет равное количество попаданий.

Ответ:

6.6. Игральная кость подбрасывается 5 раз. Найти вероятность того, что два раза появится число очков, кратное трем.

Ответ:

6.7. Экзаменационный билет состоит из пяти вопросов в виде теста с тремя возможными ответами на каждый из пяти вопросов, из которых нужно выбрать один правильный. Какова вероятность сдать экзамен методом простого угадывания, если достаточно ответить хотя бы на 4 вопроса?

Ответ:

6.8. Три охотника одновременно выстрелили по волку. Вероятности попадания каждым из охотников одинаковы и равны 0,4. Определить вероятность того, что волк будет убит, если известно, что при одном попадании охотники убивают волка с вероятностью 0,2, при двух – с вероятностью 0,5 и при трех – с вероятностью 0,8.

Ответ:

9. На контроль поступила партия деталей из цеха. Известно, что 5 % всех деталей не удовлетворяет стандарту. Сколько нужно испытать деталей, чтобы с вероятностью не менее 0,95 обнаружить хотя бы одну нестандартную деталь?

Ответ:

9. Для данного баскетболиста вероятность забросить мяч в корзину при броске равна 0,4. Произведено 10 бросков. Найти наивероятнейшее число попаданий и соответствующую вероятность.

Ответ:,.

9. Найти наивероятнейшие числа отрицательных и положительных ошибок и соответствующую вероятность при четырех измерениях, если при каждом измерении вероятность получения положительной ошибки равна 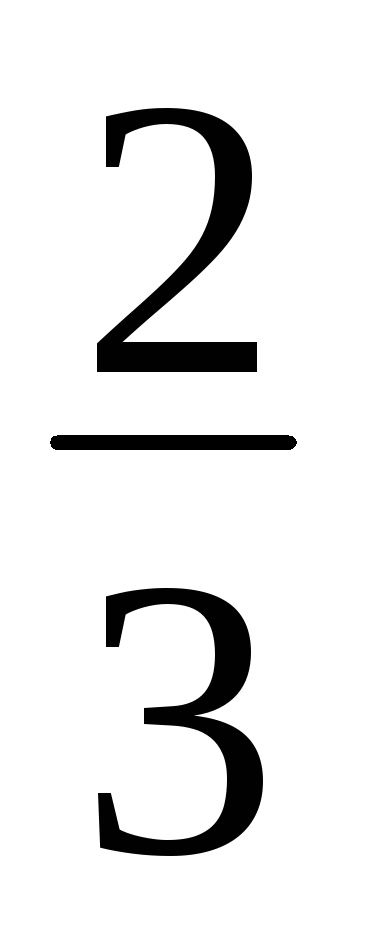, а отрицательной —.

Ответ:

9. Вероятность попадания в десятку при одном выстреле р= 0,2. Сколько нужно провести независимых выстрелов, чтобы с вероятностью не менее 0,9 попасть в десятку хотя бы один раз?

Ответ:

9. Какое наименьшее количество чисел необходимо взять из таблицы случайных чисел, чтобы с наибольшей вероятностью обеспечивалось появление среди них трех чисел, оканчивающихся цифрой 7?

Ответ:

9. Вероятность появления события в каждом из независимых испытаний равна 0,3. Найти число испытаний n, при котором наивероятнейшее число появлений события в этих испытаниях будет равно 30.

Ответ:

6.15. Доля крупных заказов в строительной фирме составляет 40%. Чему равно наивероятнейшее число крупных заказов, если фирма предполагает заключить 120 договоров на следующий год?

Ответ:.

6.16. Пусть вероятность того, что студент опоздает на лекцию, равна 0,08. Найти наиболее вероятное число опоздавших из 96 студентов.

Ответ: .

17. Чему равна вероятность рнаступления события в каждом из 49 независимых испытаний, если наивероятнейшее число наступлений события в этих испытаниях равно 30?

Ответ:

17. Чему равна вероятность рнаступления события в каждом из 39 независимых испытаний, если наивероятнейшее число наступлений события в этих испытаниях равно 25?

Ответ: