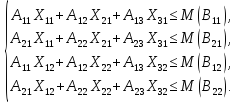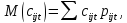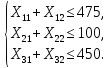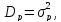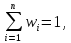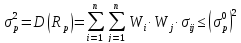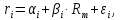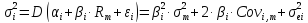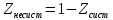Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Украинская академия банковского дела Национального банка Украины

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

писаревская.docx

Скачиваний:

Добавлен:

20.02.2016

Размер:

4.14 Mб

Скачать

☆

<<< < Предыдущая 12 / 72 3 4 5 6 7 > Следующая >>>

Завдання 2

На двох підприємствах випускаються 3 види продукції А, В, С. Прибуток від реалізації одиниці продукції кожного виду є величиною випадковою, функція розподілу якого наведена в таблицях 2.1 та 2.2.

Таблиця 2.1 – Прибуток підприємства №1 від реалізації одиниці продукції кожного виду

А		В			С
С₁₁t	P₁₁t	C₂₁t	P₂₁t	C₃₁t		P₃₁t
25	0,29	29	0,15	33		0,13
27	0,22	35	0,15	50		0,19
26	0,4	40	0,23	40		0,43
33	0,09	31	0,47	37		0,25

Таблиця 2.2 – Прибуток підприємства №2 від реалізації одиниці продукції кожного виду

А			В			С
С₁₂t	P₁₂t	C₂₂t		P₂₂t	C₃₂t		P₃₂t
18	0,14	23		0,33	26		0,02
25	0,48	40		0,22	43		0,23
23	0,32	35		0,01	27		0,41
19	0,06	33		0,44	37		0,34

Для виробництва продукції використовуються 2 види ресурсів, обсяг яких також є випадковим – функція розподілу яких наведена в таблицях 2.3-2.4.

Таблиця 2.3 – Функція розподілу обсягів споживання 2 видів ресурсів першим підприємством

1 ресурс		2 ресурс
В₁₁t	Q₁₁t	B₂₁t	Q₂₁t
1800	0,37	1000	0,13
1550	0,14	1300	0,35
1750	0,08	1400	0,17
2050	0,17	2200	0,31
1900	0,24	1275	0,04

Таблиця 2.4 – Функція розподілу обсягів споживання 2 видів ресурсів другим підприємством

1 ресурс		2 ресурс
В₁₂t	Q₁₂t	B₂₂t	Q₂₂t
1500	0,31	2600	0,33
1575	0,09	2550	0,11
1600	0,17	2375	0,22
1400	0,21	2400	0,01
1800	0,22	2625	0,33

Норми витрат на одиницю продукції відомі та задані в таблицях 2.5-2.6.

Таблиця 2.5 – Норми витрат 2 видів ресурсів на одиницю продукції першим підприємством

	1 Ресурс	2 Ресурс
А	2,7	1,1
В	4,1	3,3
С	2,9	2,1

Таблиця 2.6 – Норми витрат 2 видів ресурсів на одиницю продукції другим підприємством

	1 Рес	2 Рес
А	2,4	1,1
В	2,6	2,1
С	2,7	1,7

Також відомі обмеження за попитом на кожен вид продукції.

Таблиця 2.7 – Обмеження за попитом на кожен вид продукції першого підприємства

	Нижня межа	Верхня межа
А	21	72
В	9	110
С	37	385

Таблиця 2.8 – Обмеження за попитом на кожен вид продукції другого підприємства

	Нижня межа	Верхня межа
А	83	390
В	55	107
С	29	350

Також відомі потреби в продукції кожного виду в галузі.

Таблиця 2.9 – Потреби в продукції кожного виду в галузі

A₁	A₂	A₃
475	100	450

Розв’язання

Побудуємо економіко-математичну модель стохастичного програмування для визначення оптимального плану випуску продукції на підприємствах.

Оскільки цільова функція буде відображати прибуток, то вона буде спрямована на максимізацію і матиме наступний вигляд:

(2.1)

Для виробництва продукції використовуються 2 види ресурсів, обсяг яких також обмежений. Відповідно маємо систему обмежень на обсяг використання кожного з двох ресурсів на двох підприємствах:

(2.2)

Також відомі обмеження на верхню та нижню межу за попитом на кожен вид продукції. Відповідно маємо наступні обмеження:

(2.3)

Оскільки задані потреби в продукції кожного виду в галузі, то виробляти більше ніж буде спожито – економічно неефективно (виникають додаткові витрати на зберігання, просування також відбувається псування продукції). Звідси маємо наступну систему обмежень:

(2.4)

І звичайно ж об’єм випуску продукції не може бути від’ємним числом та обов’язково мусить бути цілим:

	(2.5)
	(2.6)

Знайдемо значення математичних сподівань з використанням можливостей табличного процесору MS Excel, застосувавши наступні формули:

(2.7)

Рисунок 2.1 – Знаходження значень математичних сподівань

Підставимо значення відомих змінних у формули математичної моделі.

(2.8)

(2.9)

(2.10)

	(2.11)
	(2.12)
	(2.13)

Для визначення оптимального плану використаємо інструмент табличного процесору MS Excel «Пошук рішення»:

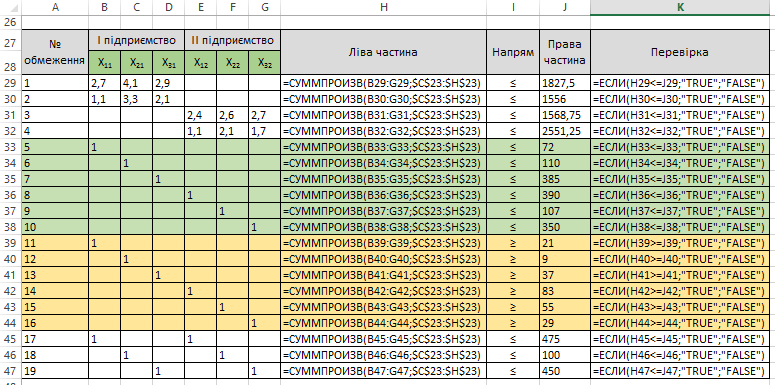
Рисунок 2.2 – Задання математичної моделі задачі в табличному процесорі MS Excel

За допомогою пакету MS Excel та стандартної функції «Пошук рішення» розв’яжемо задачу. Наведемо зображення вікна, що використовувалось для пошуку на рисунку 2.3

Рисунок 2.3 – Задання налаштувань для інструменту «Пошук рішення»

Після застосування інструменту «Пошук рішення», отримали наступні результати представлені на рис. 2.4.

Було отримано оптимальний план випуску продукції:

(2.14)

Рисунок 2.4 – Результат роботи інструменту «Пошук рішення»

Отже, для максимізації прибутку потрібно випускати І-му підприємству по 21, 9 і 37 одиниць продукції відповідно 1-го, 2-го та 3-го видів; а другому по 83, 55, 29 одиниць відповідно.

За даного оптимального плану, прибуток буде найбільший і складе 6964,67 гр. од. Усі ресурси є недефіцитними, оскільки жоден з них не використовується повністю, а вся продукція є рентабельною. Перевиробництва продукції немає.

Оцінимо міру ризику, щодо одержання максимального прибутку за загальним коефіцієнтом варіації і коефіцієнтом варіації по від’ємній семіваріації, скориставшись наступними формулами:

(2.15)

(2.16)

(2.17)

(2.18)

Значення всіх показників знайдемо використовуючи можливості табличного процесору MS Excel:

Рисунок 2.5 – Результат оцінки міри ризику, щодо одержання максимального прибутку за загальним коефіцієнтом варіації в табличному процесорі MS Excel

Рисунок 2.6 – Результат оцінки міри ризику, щодо одержання максимального прибутку за коефіцієнтом варіації по від’ємній семіваріації в MS Excel

Висновок: спираючись на отримані результати можемо стверджувати, що при реалізації даного проекту 1 грн. прибутку можемо втратити з ризиком 7,10%, що є меншими допустимого ризику (,10). При цьому можливість відхилення абсолютного значення очікуваних втрат становить 0,3%, що також є допустимою величиною.

ЗАВДАННЯ 3

Нехай інвестор свій капітал в сумі К вкладає в 3 акції (К1, К2, К3). Відома динаміка цін цих акцій за місяць на фондовому ринку.

Таблиця 3.1 – Динаміка цін акцій за місяць на фондовому ринку

Дні	Ціна акцій 1	Ціна акцій 2	Ціна акцій 3
1	48	96	98
2	90	59	70
3	30	94	90
4	80	38	27
5	45	76	59
6	44	84	61
7	29	49	30
8	87	78	53
9	62	62	64
10	86	27	102
11	56	87	31
12	102	31	66
13	102	52	49
14	98	88	103
15	81	25	49
16	55	91	39
17	62	87	39
18	102	37	71
19	89	85	43
20	97	31	32
21	68	98	59
22	27	43	97
23	72	37	80
24	86	36	73
25	72	75	80

Продовження таблиці 3.1

Дні	Ціна акцій 1	Ціна акцій 2	Ціна акцій 3
26	100	66	74
27	92	104	55
28	39	39	78
29	43	44	30
30	93	86	59

Необхідно розрахувати прибутковість сподіваної норми прибутку і ризик для трьох акцій; дати характеристику систематичного ризику для кожної акції; розрахувати сподівану норму портфелю цінних паперів і його ризик, а також оптимізувати портфель цінних паперів за моделями Марковіца та Шарпа.

Розв’язання

Постановка задачі. Нехай інвестор свій капітал в сумі К вкладає в 3 акції (К1, К2, К3). Відома динаміка цін цих акцій за місяць на фондовому ринку. Розрахувати прибутковість сподіваної норми прибутку і ризик для трьох акцій; дати характеристику систематичного ризику для кожної акції; розрахувати сподівану норму портфелю цінних паперів і його ризик, а також оптимізувати портфель цінних паперів за моделями Марковіца.

Здійснимо розрахунок прибутковості, сподіваної норми прибутку, дисперсії і стандартного відхилення для кожної акції.

Для визначення ціни акції певного періоду застосуємо функцію «Аналіз даних→Генерація випадкових чисел (66; 16)» в табличному процесорі Microsoft Excel. В результаті отримали наступні дані:

Таблиця 3.2 – Динаміка цін акцій за місяць на фондовому ринку

Дні	Ціна акцій 1	Ціна акцій 2	Ціна акцій 3
1	48	96	98
2	90	59	70
3	30	94	90
4	80	38	27
5	45	76	59
6	44	84	61
7	29	49	30
8	87	78	53
9	62	62	64
10	86	27	102
11	56	87	31
12	102	31	66
13	102	52	49
14	98	88	103
15	81	25	49
16	55	91	39
17	62	87	39
18	102	37	71
19	89	85	43
20	97	31	32
21	68	98	59
22	27	43	97
23	72	37	80
24	86	36	73
25	72	75	80
26	100	66	74
27	92	104	55
28	39	39	78
29	43	44	30
30	93	86	59

Для розрахунку прибутковості кожної акції застосуємо наступну формулу:

(3.1)

Де – ціна акції t-го періоду;

– ціна акції попереднього періоду.

Виконавши розрахунки прибутковості кожної акції, отримаємо наступні значення:

Таблиця 3.3 – Розрахунок прибутковості кожної акції за місяць на фондовому ринку

Дні		R1		R2		R3
1		-		-		-
2		87,50		-38,54		-28,57
3	-66,67		59,32		28,57
4	166,67		-59,57		-70,00
5	-43,75		100,00		118,52
6	-2,22		10,53		3,39
7	-34,09		-41,67		-50,82
8	200,00		59,18		76,67
9	-28,74		-20,51		20,75
10	38,71		-56,45		59,38
11	-34,88		222,22		-69,61
12	82,14		-64,37		112,90
13	0,00		67,74		-25,76
14	-3,92		69,23		110,20
15	-17,35		-71,59		-52,43
16	-32,10		264,00		-20,41
17	12,73		-4,40		0,00
18	64,52		-57,47		82,05

Продовження таблиці 3.3

Дні	R1	R2	R3
19	-12,75	129,73	-39,44
20	8,99	-63,53	-25,58
21	-29,90	216,13	84,38
22	-60,29	-56,12	64,41
23	166,67	-13,95	-17,53
24	19,44	-2,70	-8,75
25	-16,28	108,33	9,59
26	38,89	-12,00	-7,50
27	-8,00	57,58	-25,68
28	-57,61	-62,50	41,82
29	10,26	12,82	-61,54
30	116,28	95,45	96,67

Щоб розрахувати сподівану норму прибутку, необхідно використати наступну формулу:

(3.2)

де – ймовірність t-го періоду (стану);

– прибутковість j-ї акції t-го періоду.

Оскільки, згідно умови, нам не надана ймовірність до t-го періоду (стану), тому будемо вважати ймовірності настання кожного з станів рівно можливими та скористаємось наступною формулою для обчислення сподіваної норми прибутку:

(3.3)

Слід зауважити, що завжди повинна бути додатною величиною. Провівши розрахунки, отримали наступні значення для трьох видів акцій:

Таблиця 3.4 – Сподівана норма прибутку для трьох видів акцій


19,46	29,20	13,99

Дисперсію прибутковості кожного виду акцій, можна визначити за формулою:

(3.4)

Рисунок 3.1 – Проміжні обчислення дисперсії прибутковості кожного виду акцій в табличному процесорі MS Excel

Таблиця 3.5 – Дисперсія прибутковості кожного виду акцій

V1	V2	V3
4815,69	8384,03	3350,99

Дисперсія вказує міру невизначеності в очікуваннях інвестора, що оцінює майбутню прибутковість як середню за всіма можливими значеннями.

Стандартне (середнє квадратичне) відхилення найбільш поширений показник розсіювання значень випадкової величини відносно її математичного сподівання. Перевагою даного показника є те, що вимірюється він в одиницях виміру самої випадкової величини.

Середньоквадратичне відхилення дорівнює кореню квадратному з дисперсії випадкової величини:

(3.5)

Таблиця 3.6 – Стандартне відхилення прибутковості кожного виду акцій


69,40	91,56	57,89

Визначимо коефіцієнти коваріації між прибутками двох видів акцій. Коваріація (англ. Covariance) – в теорії ймовірностей та математичній статистиці, числова характеристика залежності випадкових величин. Сутність коваріації полягає в тому, що вона виникає внаслідок невизначеності результату перемножування двох сукупностей чисел.

В нашому випадку, для обчислення коваріації скористаємось наступною формулою:

(3.6)

Якщо , то прибутковості акцій і мають тенденцію змінюватися в одну сторону, наприклад краща, а ніж очікувана, прибутковість однієї з акцій повинна, ймовірно, спричинити кращу, а ніж очікувану, прибутковість акції іншого виду.

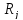Якщо , то прибутковості акцій і мають тенденцію компенсувати одна одну, наприклад краща, а ніж очікувана, прибутковість однієї з акцій супроводжується, як правило, гіршою, а ніж очікуваною, прибутковістю акції іншого виду.

Відносно невелике або нульове значення коваріації, показує, що зв’язок між прибутковістю даних акцій слабкий або відсутній взагалі.

Виконані проміжні обчислення в MS Excel представлені на рисунку 3.2:

Рисунок 3.2 – Проміжні обчислення коваріації в MS Excel

В результаті отримали наступні значення показників коваріації:

Таблиця 3.7 – Показники коваріації між кожною парою видів акцій

cov(r1,r2)	cov(r1,r3)	cov(r2,r3)
-1597,16	223,17	122,63

Перевіримо отримані значення показників коваріації за допомогою надбудови табличного процесору MS Excel «Аналіз даних»:

Рисунок 3.3 – Обчислення коваріації за допомогою надбудови «Аналіз даних»

Як бачимо показники коваріації повністю співпали, що підтверджує безпомилковість їх знаходження.

Наступним кроком буде знаходження значення коефіцієнтів кореляції. Коефіцієнт кореляції нормує коваріацію для полегшення порівняння з іншими парами випадкових змінних.

В теорії ймовірностей та математичній статистиці, кореляція є залежністю двох випадкових величин. При цьому, зміна однієї або кількох цих величин призводить до систематичної зміни іншої або інших величин. Математичною мірою кореляції двох випадкових величин слугує коефіцієнт кореляції.

Кореляція може бути позитивною та негативною (можлива також ситуація відсутності статистичного зв’язку – наприклад, для незалежних випадкових величин). Від’ємна кореляція – кореляція, при якій збільшення однієї змінної пов’язане зі зменшенням іншої, при цьому коефіцієнт кореляції від’ємний. Додатна кореляція – кореляція, при якій збільшення однієї змінної пов’язане зі збільшенням іншої, при цьому коефіцієнт кореляції додатній.

Коефіцієнт кореляції знаходиться за наступною формулою:

(3.7)

де 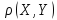– коефіцієнт кореляції випадкових величин X та Y;

– коваріація випадкових величин X та Y;

– стандартні відхилення випадкових величин X та Y.

Застосувавши дану формулу отримали наступні значення кореляції.

Таблиця 3.8 – Показники кореляції між кожною парою видів акцій

ρ₁₂	ρ₁₃	ρ₂₃
-0,25	0,06	0,02

Перевіримо отримані значення показників кореляції за допомогою надбудови табличного процесору MS Excel «Аналіз даних»:

Рисунок 3.4 – Обчислення кореляції за допомогою надбудови «Аналіз даних»

Як бачимо показники кореляції повністю співпали, що підтверджує безпомилковість їх знаходження.

Значення коефіцієнта кореляції належить інтервалу від -1 до +1. Знак коефіцієнта кореляції збігається зі знаком коваріації, тому додане його значення означає односпрямовану зміну змінних, а від’ємне – зміну в протилежних напрямках. Якщо значення коефіцієнта кореляції є близьким до нуля, то зв’язок між змінними слабкий.

Проведемо моделювання дохідності та ризику портфеля. Найбільш розповсюдженими є дві моделі визначення характеристик портфеля: модель Марковіца та модель Шарпа. Обидві моделі створені й успішно працюють в умовах, що склалися у відносно стабільних західних фондових ринках. Модель, яка здатна успішно функціонувати в умовах фондового ринку, що формується, розвивається та реорганізується, яким є фондовий ринок України, отримала назву квазі-Шарпа.

Проведемо чисельне моделювання оптимізації фондового портфеля, використовуючи модель Марковіца для розрахунку характеристик портфеля. В класичній теорії портфеля приймається гіпотеза щодо випадковості норм прибутків активів, а саме – що величини є дискретними випадковими величинами (). Ця гіпотеза дозволяє використовувати в процесі побудови моделей методи теорії ймовірності та математичної статистики.

Модель базується на тому, що показники прибутковості різних цінних паперів взаємопов’язані: із зростанням дохідності одних паперів спостерігається одночасне зростання і за іншими паперами, треті залишаються без змін, а в четвертих, навпаки, дохідність знижується. Такий вид залежності недетермінований, тобто є стохастичним, і називається кореляцією. Тобто, основна ідея моделі Марковіца полягає в тому, щоб статистично розглядати майбутній дохід, принесений фінансовим інструментом, як випадкову змінну, тобто доходи по окремих інвестиційних об’єктах випадково змінюються в деяких межах.

Якщо ж певним чином випадково визначити по кожному інвестиційному об’єкту певні ймовірності настання, можна отримати розподіл ймовірностей одержання доходу по кожній альтернативі вкладення коштів. Даний підхід отримав назву ймовірнісної моделі ринку. Для спрощення за моделлю Марковіца вважається, що доходи розподілені за нормальним законом розподілу. За моделлю Марковіца визначаються показники, що характеризують обсяг інвестицій і ризик, які дозволяють порівнювати між собою різні альтернативи вкладення капіталу з точки зору поставлених цілей і тим самим створити масштаб для оцінки різних комбінацій. В якості масштабу очікуваного доходу з ряду можливих доходів на практиці використовують найбільш ймовірне значення, яке в разі нормального розподілу збігається з математичним очікуванням.

Загалом модель Марковіца має наступні основні припущення:

за дохідність цінних паперів приймається математичне очікування дохідності;
за ризик цінних паперів приймається середньоквадратичне відхилення дохідності;
вважається, що дані минулих періодів, які використані при розрахунках дохідності і ризику, повністю відображають майбутні значення дохідності;
ступінь і характер взаємозв’язку між цінними паперами виражається коефіцієнтом лінійної кореляції.

У моделі Марковіца допустимими є лише стандартні портфелі (без коротких позицій). До останніх належать портфелі, структури яких мають елементи, що задовольняють дві умови:

(3.8)

(3.9)

Допустимі портфелі цього класу утворюють множину:

(3.10)

Математичне сподівання доходу за i-м цінним папером () розраховується наступним чином:

(3.11)

де – можливий дохід за i-м цінним папером;

– ймовірність отримання доходу;

– кількість цінних паперів.

Для вимірювання ризику слугують показники розсіювання, тому чим більший розкид величин можливих доходів, тим більше небезпека, що очікуваний дохід не буде отриманий. Мірою розсіювання є дисперсія дохідності цінного паперу або середньоквадратичне відхилення:

(3.12)

(3.13)

де – міра ризику портфелю;

– коваріація між доходностями i-го та j-го цінних паперів;

та – частки загального вкладення, що припадають на i-ий та j-ий цінні папери;

– кількість цінних паперів.

Коваріація доходностей цінних паперів (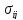) дорівнює кореляції між ними, помноженій на добуток їхніх стандартних відхилень:

(3.14)

де – коефіцієнт кореляції доходностей i-го та j-го цінних паперів;

та – стандартні відхилення доходностей i-го та j-го цінних паперів.

Для коваріація дорівнює дисперсії акції.

За моделлю Марковіца, дохідність портфеля цінних паперів – це середньозважена дохідність паперів, його складових, яка визначається формулою:

(3.15)

де – відсоткова частка i-го цінного паперу в портфелі;

– дохідність i-го цінного паперу.

– кількість цінних паперів.

Використовуючи введені позначення, класичну модель (концепцію) Марковіца задачі вибору портфеля з наперед заданими характеристиками можна подати в такому вигляді: серед елементів множини необхідно знайти елемент , де – частка капіталу, інвестованого в актив і-го виду (), щоб портфель зі структурою мав найбільшу сподівану норму прибутку та найменший ступінь ризику.

Формально економіко-математичну модель побудови портфеля можна подати у вигляді наступної двокритеріальної задачі вибору оптимального рішення:

	(3.16)
	(3.17)

за обмежень:

	(3.18)
	(3.19)

Наявність двох критеріїв суттєво ускладнює процес вибору оптимального портфеля, оскільки покращання значення одного критерію може призвести до погіршання значення другого. Перейдемо до висвітлення проблеми формування допустимих портфелів, віднесених до ефективних. Ефективність портфелю будемо розглядати використовуючи принцип Парето.

Оптимум Парето – це такий стан системи, при якому значення кожного окремого критерію, що описує стан системи, не може бути покращено без погіршення становища інших елементів.

Принцип, за словами Вільфредо Парето проголошує: «Слід вважати, що будь-яка зміна, яка нікому не завдає збитків і яка приносить людям користь (за їх власною оцінкою), є поліпшенням». Таким чином визнається право на всі зміни, які не приносять нікому додаткової шкоди.

Множина станів системи, оптимальних за Парето, називають «множиною Парето», «множиною альтернатив, оптимальних в сенсі Парето», або «множиною оптимальних альтернатив».

Ситуація, коли досягнута ефективність за Парето – це ситуація, коли всі вигоди від змін вичерпані.

Портфель зі сподіваною нормою прибутку та ступенем ризику називається ефективним (оптимальним за Парето), а його структура – вектором Парето (для даного портфеля), якщо для всіх портфелів, що мають структуру сподівану норму прибутку та ризик .

Аналогічно портфель зі структурою є оптимальним за Парето, а його структура – вектором Парето, якщо за його ступінь ризику .

Портфель зі структурою будемо називати ефективним в концепції Марковіца, якщо є вектором Парето задачі (3.13) - (3.16) і при цьому множина структур усіх ефективних портфелів збігається з множиною Парето задачі (3.13) - (3.16).

Якщо через , позначити множину структур усіх ефективних портфелів, то очевидно, що .

Згідно з наведеними означеннями допустимий портфель називається ефективним, якщо не існує іншого допустимого портфеля з не меншою сподіваною нормою прибутку і меншим ступенем ризику або з більшою сподіваною нормою прибутку і не більшим ступенем ризику. Ефективність портфеля означає неможливість його покращення (неможливість покращення його числових характеристик). Щодо ефективного портфеля, то будь-який інший (незбіжний з ним) портфель має або більший ступінь ризику, або меншу сподівану норму прибутку. Такій властивості портфеля, як ефективність, можна надати наочної геометричної інтерпретації (рис. 3.3), якщо у двовимірному евклідовому просторі критеріїв (критеріальному просторі) «» вздовж однієї координатної осі відкладати сподівану норму дохідності портфеля, а вздовж другої – його ризик:

Рисунок 3.5 – Допустимі та ефективні множини

Якщо скористатися принципом виділення основного критерію, то задачу пошуку ефективного портфеля (3.13)-(3.16) можна розглядати як такі дві задачі на умовний екстремум:

	(3.20)
	(3.21)
	(3.22)
	(3.23)

або

	(3.24)
	(3.25)
	(3.26)
	(3.27)

Задача (3.20)-(3.23) має рішення за всіх заданих рівнів сподіваної норми прибутку портфеля (), що задовольняють умову:

(3.28)

У свою чергу задача (3.24)-(3.27) має рішення за всіх заданих ступенів ризику портфеля (), що задовольняють умову:

(3.29)

За допомогою моделей Марковіца ми можемо визначати, який капітал вкладати на закупівлю тих чи інших акцій, щоб отримати бажані результати. У даній задачі розглянемо 3 варіанти оптимізації капіталовкладень в акції:

мінімізація ризику портфеля на множині всіх допустимих портфелів (так звана «задача збереження капіталу»);
мінімізація ризику портфеля на множині всіх допустимих портфелів за умови нижньої межі прибутковості (модель бажаного прибутку);
максимізація прибутковості портфеля на множині всіх допустимих портфелів за умови верхньої межі ризику.

Побудуємо першу модель засобами табличного процесору MS Excel:

Рисунок 3.6 – Зображення листа MS Excel з побудованою моделлю Марковіца

Рисунок 3.8 – Зображення формул побудованої моделі Марковіца на листі MS Excel

Скористаємось надбудовою MS Excel «Пошук рішення». Для знаходження рішення, задамо у вікні налаштувань надбудови необхідні нам параметри моделі:

Рисунок 3.9 – Налаштування параметрів пошуку рішення

Рисунок 3.10 – Результати пошуку рішення за першою моделлю Марковіца

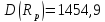Згідно з рис. 3.10, ми побудували оптимальний за Парето портфель зі структурою , який має найменший ступінь ризику та 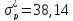. За даних параметрів ефективного портфелю, сподівана норма прибутку портфеля буде рівна

Побудуємо другу модель – модель мінімізації ризику портфеля на множині всіх допустимих портфелів за умови нижньої межі прибутковості, засобами табличного процесору MS Excel.

Рисунок 3.11 – Зображення листа MS Excel з побудованою моделлю Марковіца

Будемо знаходити рішення моделі за умови нижньої межі прибутковості рівній

Рисунок 3.12 – Зображення формул побудованої моделі Марковіца на листі MS Excel

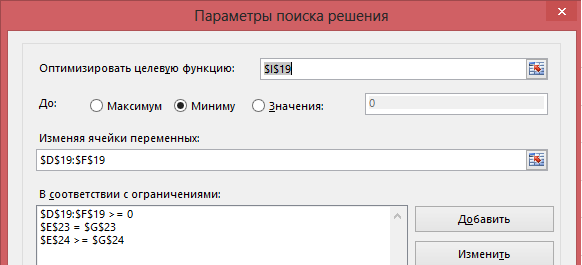
Рисунок 3.13 – Налаштування параметрів пошуку рішення

Рисунок 3.14 – Результати пошуку рішення за другою моделлю Марковіца

Згідно з рис. 3.14, ми побудували оптимальний за Парето портфель зі структурою , який має найменший ступінь ризику та , за умови нижньої межі прибутковості портфеля

Побудуємо третю модель – модель максимізації прибутковості портфеля на множині всіх допустимих портфелів за умови верхньої межі ризику, засобами табличного процесору MS Excel.

Рисунок 3.15 – Зображення листа MS Excel з побудованою моделлю Марковіца

Будемо знаходити рішення моделі за умови верхньої межі ризику рівній 40%: або .

Рисунок 3.16 – Зображення формул побудованої моделі Марковіца на листі MS Excel

Рисунок 3.17 – Налаштування параметрів пошуку рішення

Рисунок 3.18 – Результати пошуку рішення за третьою моделлю Марковіца

Згідно з рис. 3.18, ми побудували оптимальний за Парето портфель зі структурою , який має найбільшу прибутковість , за умови верхньої межі ризику рівній 40%: або .

Підведемо підсумки побудови ефективного портфелю за моделями Марковіца побудувавши узагальнену таблицю результатів (таблиця 3.9).

Таблиця 3.9 – Структури оптимального портфеля за моделями Марковіца

	Структура портфелю
	Модель 1	Модель 2	Модель 3
Вимоги Акції	Найменший ризик	Прибутковість не менше 10%	Ризик не більше 40%
Акція №1	36,2%	36,2%	40,1%
Акція №2	23,7%	23,7%	34%
Акція №3	40,1%	40,1%	25,9%
Характеристики оптимального портфелю	Прибутковість 8,3%, ризик 28,2%	Прибутковість 10%, ризик 38%	Прибутковість 10,1%, ризик 40%

Підводячи висновки по аналізованим даним прибутковості акцій, сподівана норма прибутку для кожної акції за місяць є позитивною: для першої акції вона складає 6,8%, для другої – 8,3 %., а для третьої – 10,6%.

Дисперсія вказує на величину ризикованості акції – найменш ризикованою є третя акція –3350,99, найризикованішою є друга акція –8384,03, середній ризик прибутковості має друга акція – 4815,69.

Коваріація вказує на прибутковість 2-хакцій. Отже, прибутковість першої і другої акції буде складати : -1597,16 (збиткові) , першої і третьої акції – 223,17, другої та третьої – 122,63. Коефіцієнти кореляції показують залежність між даними: додатне значення показника кореляції означає пряму залежність, від’ємна – обернену. В нашому випадку: для першої з другою акцій коефіцієнт кореляції -0,25 (спостерігається обернена залежність), для першої та третьої 0,06 (пряма), а для другої і третьої – 0,02 (пряма).

Дослідивши оптимізацію цінних паперів за моделями Марковіца, можна зробити такі висновки:

у будь-якому випадку ризик капіталовкладень буде дорівнювати 1454,88, при цьому необхідно зробити капіталовкладення в акції у таких пропорціях – у першу вкласти 0,362, у другу – 0,237 та у третю – 0,401.
у разі, якщо інвестор захоче максимізувати сподівану норму портфелю та зробити ризик величиною не більше сталої (певної константи σ = 40),тоді необхідно буде зробити капіталовкладення в акції у таких пропорціях – у першу – 0,401, у другу – 0,4, а у третю – 0,259, при цьому сподівана норма прибутковості портфелю складе 21,35.

Проведемо аналіз за моделлю Шарпа. Як випливає з моделі Марковіца, задавати розподіл доходів окремих цінних паперів не потрібно, досить лише визначити величини, що характеризують даний розподіл: математичне сподівання, середньоквадратичне відхилення і коваріацію між доходностями окремих цінних паперів. На практиці для порівняно невеликого числа цінних паперів провести такі розрахунки по визначенню очікуваного доходу і дисперсії можливо. При визначенні ж коефіцієнта кореляції трудомісткість досить велика.

У 1960-х роках Вільям Шарп першим провів регресійний аналіз ринку акцій США. Для уникнення високої трудомісткості Шарп запропонував індексну модель. Причому він не розробив нового методу складання портфеля, а спростив проблему таким чином, що наближене рішення може бути знайдене зі значно меншими зусиллями. Шарп ввів β-фактор, який відіграє особливу роль в сучасній теорії портфеля.

На відміну від моделі Марковіца, яка розглядає взаємозв’язок дохідності цінних паперів, модель Шарпа розглядає взаємозв’язок дохідності кожного цінного паперу з дохідністю ринку в цілому.

Основними припущення моделі Шарпа є наступні:

як дохідність цінного паперу береться математичне очікування дохідності;
існує деяка безризикова ставка дохідності , тобто дохідність певного цінного паперу, ризик якого завжди мінімальний порівняно з іншими цінними паперами;
взаємозв’язок відхилень дохідності цінного паперу від безризикової ставки дохідності (відхилення дохідності цінного папера) з відхиленням дохідності ринку в цілому від безризикової ставки дохідності (відхилення дохідності ринку) описується функцією лінійної регресії;
під ризиком цінного паперу слід розуміти ступінь залежності змін дохідності цінного паперу від змін дохідності ринку в цілому;
вважається, що дані минулих періодів, які використовуються при розрахунку дохідності та ризику, відображають, повною мірою, майбутні значення дохідності.

За моделлю Шарпа, відхилення дохідності цінного паперу пов’язуються з відхиленнями дохідності ринку функцією лінійної регресії наступного виду:

(3.30)

де – відхилення доходності цінного папера від безризикового;

– відхилення доходності ринку від безризикового;

– коефіцієнти регресії;

– випадкова незалежна змінна (похибка).

Похибка показує специфічний ризик активу, який не можна пояснити дією ринкових сил. Значення її середньої рівне нулю. Вона має постійну дисперсію; коваріацію з прибутковістю ринку рівну нулю; коваріацію з неринковим компонентом прибутковості інших активів рівну нулю.

Побудуємо спрощену модель, не враховуючи відхилення від безризикової ставки дохідності :

(3.31)

де 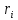– дохідність цінного папера;

– дохідність ринку;

– коефіцієнти регресії;

– випадкова незалежна змінна (похибка).

Виходячи з формули (3.31), можна по прогнозованій доходності ринку цінних паперів у цілому розрахувати дохідність будь-якого цінного папера, що його складає:

(3.32)

де – коефіцієнти регресії, що характеризують даний цінний папір.

З рівняння видно, що прибутковість цінного паперу складається з трьох компонентів:

ринкова (систематична) компонента, представлена добутком прибутковості ринкового індексу на -коефіцієнт;
власна (несистематична) компонента, представлена -коефіцієнтом;
випадкова величина (похибка).

Теоретично, якщо ринок цінних паперів перебуває у рівновазі, то коефіцієнт дорівнюватиме нулю. Але оскільки на практиці ринок завжди розбалансований, то показує надлишкову дохідність даного цінного папера (позитивну чи негативну), тобто наскільки даний цінний папір переоцінюється або недооцінюється інвесторами.

Коефіцієнт називають 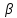-ризиком, оскільки він характеризує ступінь залежності відхилень доходності цінного папера від відхилень доходності ринку в цілому. Основні переваги моделі Шарпа – математично обґрунтована взаємозалежність доходності та ризику: чим більший -ризик, тим вища дохідність цінного папера.

Модель Шарпа має певну особливість: існує небезпека, що оцінюване відхилення доходності цінного папера не належатиме побудованій лінії регресії. Даний ризик називають залишковим ризиком.

Залишковий ризик характеризує ступінь розкиду значень відхилень доходності цінного папера навколо лінії регресії. Залишковий ризик визначають як середньоквадратичну відстань від точок доходності цінного папера до лінії регресії. Залишковий ризик і-го цінного папера позначають . Іншими словами, ризикованість вкладення коштів у даний цінний папір визначається -ризиком та залишковим ризиком .

Виходячи з ринкової моделі, загальний ризик i-го цінного паперу, вимірюється його дисперсією та позначається як :

(3.33)

де – дисперсія дохідності ринку;

– дисперсія випадкової похибки дохідності цінного паперу;

– коваріацію між дохідністю ринку та i-го цінного паперу.

Ризик i-го цінного паперу складається з двох частин: ринкового (систематичного) ризику та власного (несистематичного) ризику – .

За моделлю Шарпа дохідність портфеля цінних паперів визначається за формулою:

(3.34)

де – частка вкладення в i-й цінний папір;

– очікувана дохідність від вкладення в i-й цінний папір.

Загальний ризик інвестиційного портфеля цінних паперів може бути знайдений за допомогою формули:

(3.35)

де – частка вкладення в i-й цінний папір;

– дисперсія i-го цінного паперу;

– коефіцієнт кореляції між дохідностями i-го та j-го цінних паперів.

Окрім того, формулу (3.36) можна записати у вигляді:

(3.36)

де – для .

При різних стадіях ринку (зростаючий, спадний) для досягнення кращого ефекту можна користуватися наступними комбінаціями коефіцієнтів:

Таблиця 3.10 – Комбінації коефіцієнтів регресійного аналізу

	На покупку	На продаж
Спадний ринок
Зростаючий ринок

На західних ринках значення , , регулярно розраховуються для всіх цінних паперів і публікуються разом з індексами. Користуючись даною інформацією, інвестор може сформувати власний портфель цінних паперів.

Побудуємо та проаналізуємо модель Шарпа для наступних даних:

Таблиця 3.11 – Дохідність акцій та ринку в цілому за місяць

t	R1	R2	R3	R
1	-	-	-	-
2	62,0082	32,1931	49,6940	48,3450
3	17,9471	30,4169	50,3486	30,0416
4	63,0031	51,4823	38,4738	51,6273
5	20,5259	21,5452	21,9648	55,3689
6	40,8909	32,9698	18,2782	30,2293
7	58,2056	55,4284	27,4139	24,1820
8	59,6338	59,1867	18,2736	16,3800
9	25,1235	27,1820	48,7174	38,2602
10	20,3565	57,4197	64,6068	57,6227
11	50,7316	32,2526	48,1818	64,7838
12	59,2005	56,1578	61,0636	24,8137
13	25,7613	38,4754	52,1827	34,9810
14	51,4244	22,7873	25,9872	51,3999
15	34,4606	39,3985	41,1991	24,0096
16	21,7543	32,5426	35,4494	53,9055
17	43,0638	38,8584	46,1126	62,0875
18	60,9934	18,6902	22,6469	33,7053
19	44,5211	16,7935	50,7377	26,8661
20	48,8578	53,9849	33,5802	60,0275
21	59,4736	26,3198	50,6110	17,0865
22	33,0919	63,3571	38,9652	34,2058
23	43,4804	22,0457	18,0356	57,4365
24	64,8189	17,8586	52,3903	35,1977
25	50,4981	19,6485	23,3717	34,7002
26	40,1310	59,8719	54,7371	46,3354
27	52,6008	36,6885	62,5667	65,1348
28	47,9544	59,5316	24,8412	63,3327

Продовження таблиці 3.11

t	R1	R2	R3	R
29	65,9634	64,6831	40,9443	43,1020
30	24,1423	52,4406	26,4114	33,5451

Скористаємося вбудованою функції «ЛИНЕЙН» табличного процесору MS Excel. Вона розраховує статистику ряду із застосуванням методу найменших квадратів (МНК), щоб обчислити пряму лінію, яка найкращим чином апроксимує існуючі дані. Функція «ЛИНЕЙН» повертає масив, який описує отриману регресійну пряму. Оскільки повертається масив значень, функція повинна задаватися у вигляді формули масиву.

Рівняння для прямої лінії має вигляд:

(3.37)

або у разі декількох діапазонів значень :

(3.38)

де – залежне значення, функція від незалежного значення ;

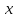– коефіцієнти, що відповідають кожній незалежній змінній x;

– постійна величина (константа).

Зауважимо, що , і можуть бути векторами. Функція «ЛИНЕЙН» повертає масив {m_n; m_n-1; ...; m₁; b}. Дана функція може також повертати додаткову регресійну статистику.

Синтаксис функції «ЛИНЕЙН» наступний:

(3.39)

де – множина значень , які вже відомі для співвідношення (3.37);

– необов’язкова множина значень , які вже відомі для співвідношення (3.37). Масив може містити одну або декілька множин змінних. Якщо використовується лише одна змінна, то та можуть мати будь-яку форму, за умови, що вони мають однакову розмірність. Якщо використовується більше однієї змінної, то повинні бути вектором (тобто інтервалом висотою в один рядок або шириною в один стовпець). Якщо опущені, то передбачається, що це масив {1; 2; 3; ...} такого ж розміру, як і .

– це логічне значення, яке вказує, чи потрібно, щоб константа дорівнювала 0. Якщо константа має значення TRUE або опущено, то обчислюється звичайним чином. Якщо константа має значення FALSE, то 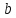вважається рівним 0 і значення підбираються так, щоб виконувалося співвідношення:

(3.40)

– це логічне значення, яке вказує, чи потрібно повернути додаткову статистику по регресії. Якщо аргумент має значення TRUE, функція «ЛИНЕЙН» повертає додаткову регресійну статистику, так що повертається масив матиме вигляд: {m_n; m_n-1; ...; m₁; b: se_n; se_n-1; ...; se₁; se_b: r2; se_y: F; df: ssreg; ssresid}.

Якщо аргумент має значення FALSE або опущений, то функція «ЛИНЕЙН» повертає лише коефіцієнти m і постійну .

За допомогою вбудованої функції «ЛИНЕЙН» табличного процесору MS Excel знайдемо наступні значення регресійних статистик, що наведені в таблиці 3.12, та подані нижче:

Таблиця 3.12 – Формат регресійних статистик, що повертає функція «ЛИНЕЙН»

β	α
σ_β	σ_α
R²
F	27

Рисунок 3.19 – Результати побудови регресійних моделей в MS Excel за допомогою функції «ЛИНЕЙН»

Отримали наступні рівняння регресії для трьох моделей:

	(3.41)

	(3.42)

	(3.43)

Для визначення питомої ваги систематичного ризику акції, обчислимо частку дисперсії її дохідності, яка визначається ринком. Скористаємось коефіцієнтом детермінації (). Він являє собою відношення дисперсії акції, що пояснюється ринком до її загальної дисперсії.

(3.44)

Таблиця 3.13 – Питома вага систематичного ризику:

Z(1)1	0,0463
Z(1)2	0,0028
Z(1)3	0,0114

Питома вага несистематичного ризику:

(3.45)

Таблиця 3.14 – Питома вага несистематичного ризику:

Z(2)1	0,9537
Z(2)2	0,9972
Z(2)3	0,9886

Отже, проводячи розрахунки по моделі Шарпа, можна зробити такі висновки: міра зв’язку між біржовим курсом першої акції і загальним станом ринку складає -0,1167, між курсом другої акції та загальним станом ринку – 0,0265, а між курсом третьої акції та загальним станом ринку – 0,0645. Також можна казати про те, що доля систематичного ризику для кожної акції є досить малою.

Основним недоліком моделі Шарпа є необхідність прогнозувати дохідність фондового ринку та безризикову ставку дохідності. Модель не враховує ризик коливань безризикової дохідності. Крім того, при значній зміні співвідношення між безризиковою дохідністю та дохідністю фондового ринку модель дає похибки. Таким чином, модель Шарпа може застосовуватися при розгляді великої кількості цінних паперів, що описують велику частку відносно стабільного фондового ринку.

ЗАВДАННЯ 4

Вантаж доставляється з пункту 1 в пункт 14 через перевалочні пункти. Відстань між пунктами вказані на графі. Виконати правильну нумерацію графу. Побудувати мінімальне дерево-остов. Визначити кількість шляхів від пункту 1 в пункт 14,що складаються із 5-ти, 6-ти та 7-ми дуг та виявити ці шляхи. За допомогою алгоритму Дейкстри знайти шлях мінімальної довжини між 1 та 14 та його довжину. За допомогою алгоритму Флойда знайти всі найкоротші шляхи.

Рисунок 4.1 – Вхідний граф

Для даного мережевого графіка знайти всі повні шляхи, критичний шлях; розрахувати ранні та пізні строки звершення подій, початку та завершення робіт; встановити резерви повних шляхів та подій, резерви часу (повні, часткові резерви першого типу, вільні та незалежні) робіт та коефіцієнти напруженості робіт.

Розв’язання

Граф – це сукупність об’єктів із зв’язками між ними. Об’єкти розглядаються як вершини, або вузли графу, а зв’язки – як дуги, або ребра. Для різних областей використання види графів можуть відрізнятися орієнтовністю, обмеженнями на кількість зв’язків і додатковими даними про вершини або ребра.

Велика кількість структур, які мають практичну цінність в математиці та інформатиці, можуть бути представлені графами.

Першою працею з теорії графів як математичної дисципліни вважають статтю Леонарда Ейлера (1736), у якій розглядалася задача про Кенігсбергські мости. Наступний імпульс теорія графів отримала близько 100 років потому з розвитком досліджень по електричним мережам, кристалографії, органічній хімії та іншим наукам.

Граф (геометричний граф) – це фігура на площині, яка складається з непорожньої скінченної множини V точок (вершин) і скінченної множини E орієнтованих чи не орієнтованих ліній (ребер), що з’єднують деякі пари вершин.

В нашому випадку дано граф, який містить дуги, такий граф називається орієнтованим. Орієнтований граф на рисунку 4.1, називається безконтурним, тому що він не має контурів. Контур – це цикл без повторення вершин, за винятком першої вершини, що збігається з останньою.

Згідно завдання, необхідно здійснити правильну нумерацію вершин графу. Будь безконтурний граф має наступну властивість: його вершини можна перенумерувати так, що будь-яка дуга буде йти від вершини з меншим номером до вершини з більшим номером, саме така нумерація називається правильною.

Доказом даної властивості слугує алгоритм правильної нумерації («алгоритмом викреслення дуг»). Алгоритм ґрунтується на наступному факті: в безконтурному графі існує хоча б одна вершина, до якої не заходить жодна дуга (інакше б у графі існував контур). Всі подібні вершини збираються в стек. Після чого виконуються наступні етапи:

1) з стеку виштовхується вершина;

2) даній вершині присвоюється наступний номер;

3) дана вершина видаляється з графу разом з усіма дугами, що виходять з неї.

Етапи 1-3 повторюються доти, доки зі стеку не буде вилучена остання вершина. Після чого, можуть з’явитися нові вершини, в які не заходить жодна дуга. Дані вершини знову поміщаються до стеку і вже для них виконуються етапи 1-3.

Зрозуміло, що в результаті вийде правильна нумерація, так як будь-яка вершина u отримує номер в той момент, коли залишилися ще незанумеровані вершини v (пізніше вони отримають більші номери).

При видаленні з безконтурного графа вершин і дуг завжди виходить безконтурний граф, а в ньому існує хоча б одна вершина без дуг, що входять в неї. Тому кожна вершина обов’язково потрапить в стек і отримає відповідний номер.

У вхідному графі, можемо виділити лише одну вершину, в котру не входить жодна дуга.

Рисунок 4.2 – Визначення першої вершини

Видаливши дану вершину та відповідні їй дуги отримаємо наступний граф:

Рисунок 4.3 – Визначення другої вершини

Аналогічно здійснимо визначення номерів наступних вершин графа та наведемо вже пронумерований граф на рисунку 4.4:

Рисунок 4.4 – Результат виконання правильної нумерації графа

Мінімальне остовне дерево (або мінімальне покриваюче дерево) в зв’язаному,зваженому, неорієнтованому графі – це остовне дерево цього графа, яка має мінімальну можливу вагу, де під вагою дерева розуміється сума ваг ребер, що входять до нього.

Існує декілька алгоритмів для знаходження мінімального остовного дерева. Найбільш відомими з них є перераховані нижче:

алгоритм Прима;
алгоритм Краскала (або алгоритм Крускала);
алгоритм Борувкі.

Алгоритм Прима – алгоритм побудови мінімального остовного дерева зваженого зв’язаного неорієнтованого графа. Алгоритм вперше був відкритий в 1930 році чеським математиком Войцехом Ярніком, пізніше перевідкритий Робертом Примом в 1957 році, і, незалежно від них, Е. Дейкстрой в 1959 році.

Побудова починається з дерева, що включає в себе одну (довільну) вершину. Протягом роботи алгоритму дерево розростається, поки не охопить всі вершини вихідного графа. На кожному кроці алгоритму до поточного дереву приєднується найлегше з ребер, що з’єднують вершину з побудованого дерева, і вершину не з дерева.

Алгоритм Борувкі – це алгоритм знаходження мінімального остовного дерева в графі. Вперше був опублікований в 1926 році Отакаром Борувкой як метод знаходження оптимальної електричної мережі в Моравії. Кілька разів був перевідкритий, наприклад Флореком, Перкалом і Солліном. Останній, крім того, був єдиним західним ученим з цього списку, і тому алгоритм часто називають алгоритмом Солліна, особливо в літературі з паралельним обчисленням.

Алгоритм Крускала (або алгоритм Краскала) – алгоритм побудови мінімального остовного дерева зваженого зв’язкового неорієнтованого графа. Алгоритм вперше описаний Джозефом Крускалом в 1956 році.

Спочатку поточна множина ребер встановлюється порожньою. Після чого, доки це можливо, проводиться наступна операція: з усіх ребер, додавання яких до вже наявної множини не викличе появу в ньому циклу, вибирається ребро мінімальної ваги і додається до вже наявної множини. Коли таких ребер більше немає, алгоритм завершено. Підграф даного графа, що містить усі його вершини і знайдена множина ребер, є його остовним деревом мінімальної ваги.

Для початку сформуємо список дуг графа.

Таблиця 4.1 – Список дуг графа

№	Дуга	Вага
1	(1;2)	8
2	(1;3)	3
3	(1;4)	4
4	(2;3)	3
5	(2;4)	3
6	(2;5)	2
7	(2;6)	9
8	(3;5)	8
9	(4;6)	1
10	(4;8)		5
11	(5;6)		5
12	(5;9)		7
13	(6;7)		6
14	(6;8)		7
15	(6;9)		2
16	(6;10)		3
17	(7;9)		3
18	(7;10)		2
19	(7;12)		5
20	(8;10)		6
21	(9;11)		5
22	(9;12)		2
23	(10;12)		3
24	(10;13)		6
25	(11;12)		3
26	(11;14)		6
27	(12;13)		3
28	(12;14)		8
29	(13;14)		5

Відсортуємо сформований список дуг графа по зростанню вагів.

Таблиця 4.2 – Відсортований список дуг графа по зростанню вагів

№	Дуга	Вага
1	(4;6)	1
2	(2;5)	2
3	(6;9)	2
4	(7;10)	2
5	(9;12)	2
6	(1;3)		3
7	(2;3)		3
8	(2;4)		3
9	(6;10)		3
10	(7;9)		3
11	(10;12)		3
12	(11;12)		3
13	(12;13)		3
14	(1;4)		4
15	(4;8)		5
16	(5;6)		5
17	(7;12)		5
18	(9;11)		5
19	(13;14)		5
20	(6;7)		6
21	(8;10)		6
22	(10;13)		6
23	(11;14)		6
24	(5;9)		7
25	(6;8)		7
26	(1;2)		8
27	(3;5)		8
28	(12;14)		8
29	(2;6)		9

Вважаємо, що кожна вершина відноситься до своєї компоненти зв’язності. Проходимо ребра в «відсортованому» порядку. Для кожного ребра виконуємо наступну перевірку:

якщо вершини, що сполучаються даним ребром, лежать в різних компонентах зв’язності, то об’єднуємо ці компоненти в одну, а дане ребро додаємо до мінімального дерева-остову;
якщо вершини, що сполучаються даним ребром, лежать в одній компоненті зв’язності, то виключаємо ребро з розгляду, оскільки при включенні даного ребра утворюється цикл.

Включаємо в дерево-остов ребро (4, 6). Множина вершин, включених в дерево-остов V={4, 6}.

Рисунок 4.5 – Результат включення першого ребра до остового дерева

Включаємо в дерево-остов ребро (2, 5). Множина вершин, включених в дерево-остов V={2, 4, 5, 6}.

Рисунок 4.6 – Результат включення другого ребра до остового дерева

Включаємо в дерево-остов ребро (6, 9). Множина вершин, включених в дерево-остов V={ 2, 4, 5, 6, 9}.

Рисунок 4.7 – Результат включення третього ребра до остового дерева

Аналогічно до проведених операцій та згідно алгоритму розв’яжемо задачу. Результат наведено на рисунку 4.8

Рисунок 4.8 – Результат включення тринадцятого ребра до остового дерева

Таблиця 4.3 – Включення дуг графа до остового дерева

№	Дуга	Вага	Включати в остове дерево
1	(4;6)	1	+
2	(2;5)	2	+
3	(6;9)	2	+
4	(7;10)	2	+

Продовження таблиці 4.3

№	Дуга	Вага			Включати в остове дерево
5	(9;12)	2			+
6	(1;3)	3			+
7	(2;3)	3			+
8	(2;4)	3			+
9	(6;10)	3			+
10	(7;9)	3			-
11	(10;12)	3			-
12	(11;12)	3			+
13	(12;13)	3			+
14	(1;4)	4			-
15	(4;8)	5			+
16	(5;6)	5			-
17	(7;12)		5	-
18	(9;11)		5	-
19	(13;14)		5	+
20	(6;7)		6	-
21	(8;10)		6	-
22	(10;13)		6	+
23	(11;14)		6	-
24	(5;9)		7	-
25	(6;8)		7	-
26	(1;2)		8	-
27	(3;5)		8	-
28	(12;14)		8	-
29	(2;6)		9	-

Наступним завданням є визначення кількості шляхів від пункту 1 в пункт 14, що складаються із 5-ти, 6-ти та 7-ми дуг та виявлення цих шляхів.

Для визначення кількості шляхів, що складаються з k дуг, необхідно матрицю суміжності 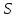піднести до k-го степеня . Тоді значення елемента , буде дорівнювати кількості шляхів довжини k із вершини до вершини .

Побудуємо матрицю суміжності для заданого графу та піднесемо її відповідно до 5-го, 6-го та 7-го степенів скориставшись засобами MathCAD.

		1	2	3	4	5	6	7	8	9	10	11	12	13	14
	1	0	1	1	1	0	0	0	0	0	0	0	0	0	0
	2	0	0	1	1	1	1	0	0	0	0	0	0	0	0
	3	0	0	0	0	1	0	0	0	0	0	0	0	0	0
	4	0	0	0	0	0	1	0	1	0	0	0	0	0	0
	5	0	0	0	0	0	1	0	0	1	0	0	0	0	0
	6	0	0	0	0	0	0	1	1	1	1	0	0	0	0
S¹=	7	0	0	0	0	0	0	0	0	1	1	0	1	0	0
	8	0	0	0	0	0	0	0	0	0	1	0	0	0	0
	9	0	0	0	0	0	0	0	0	0	0	1	1	0	0
	10	0	0	0	0	0	0	0	0	0	0	0	1	1	0
	11	0	0	0	0	0	0	0	0	0	0	0	1	0	1
	12	0	0	0	0	0	0	0	0	0	0	0	0	1	1
	13	0	0	0	0	0	0	0	0	0	0	0	0	0	1
	14	0	0	0	0	0	0	0	0	0	0	0	0	0	0

Рисунок 4.25 – Матриця суміжності S вхідного графу

		1	2	3	4	5	6	7	8	9	10	11	12	13	14
	1	0	0	0	0	0	0	1	1	4	7	6	21	17	16
	2	0	0	0	0	0	0	0	0	1	2	3	13	18	26
	3	0	0	0	0	0	0	0	0	0	0	1	4	6	7
	4	0	0	0	0	0	0	0	0	0	0	0	1	4	11
	5	0	0	0	0	0	0	0	0	0	0	0	1	4	11
	6	0	0	0	0	0	0	0	0	0	0	0	0	1	5
S⁵=	7	0	0	0	0	0	0	0	0	0	0	0	0	0	1
	8	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	9	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	10	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	11	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	12	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	13	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	14	0	0	0	0	0	0	0	0	0	0	0	0	0	0

Рисунок 4.26 – Матриця суміжності S в 5-му степені

Значення означає, що з вершини 1 у вершину 14 існує 16 шляхів довжиною в 5 ребер.

		1	2	3	4	5	6	7	8	9	10	11	12	13	14
	1	0	0	0	0	0	0	0	0	1	2	4	18	28	44
	2	0	0	0	0	0	0	0	0	0	0	1	6	15	34
	3	0	0	0	0	0	0	0	0	0	0	0	1	4	11
	4	0	0	0	0	0	0	0	0	0	0	0	0	1	5
	5	0	0	0	0	0	0	0	0	0	0	0	0	1	5
	6	0	0	0	0	0	0	0	0	0	0	0	0	0	1
S⁶=	7	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	8	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	9	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	10	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	11	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	12	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	13	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	14	0	0	0	0	0	0	0	0	0	0	0	0	0	0

Рисунок 4.27 – Матриця суміжності S в 6-му степені

З вершини 1 у вершину 14 існує 44 шляхів довжиною в 6 ребер.

		1	2	3	4	5	6	7	8	9	10	11	12	13	14
	1	0	0	0	0	0	0	0	0	0	0	1	7	20	50
	2	0	0	0	0	0	0	0	0	0	0	0	1	6	22
	3	0	0	0	0	0	0	0	0	0	0	0	0	1	5
	4	0	0	0	0	0	0	0	0	0	0	0	0	0	1
	5	0	0	0	0	0	0	0	0	0	0	0	0	0	1
	6	0	0	0	0	0	0	0	0	0	0	0	0	0	0
S⁷=	7	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	8	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	9	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	10	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	11	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	12	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	13	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	14	0	0	0	0	0	0	0	0	0	0	0	0	0	0

Рисунок 4.28 – Матриця суміжності S в 7-му степені

Значення означає, що з вершини 1 у вершину 14 існує 50 шляхів довжиною в 7 ребер.

Щоб виявити дані шляхи, слід позначити дуги, наприклад , де i – номер вершини з якої виходить дуга, а j – номер вершини куди заходить дуга. Результат позначення представлено на рис. 4.29.

Рисунок 4.9 – Позначення дуг вхідного графа

Наступним етапом буде, введення до розгляду замість матриці суміжності, матрицю, елементами якої є дуги вигляду .

Виконаэмо символьне множення матриць та розглянемо елементи , та .

		1	2	3	4	5	6	7	8	9	10	11	12	13	14
	1	0	u_1,2	u_1,3	u_1,4	0	0	0	0	0	0	0	0	0	0
	2	0	0	u_2,3	u_2,4	u_2,5	u_2,6	0	0	0	0	0	0	0	0
	3	0	0	0	0	u_3,5	0	0	0	0	0	0	0	0	0
	4	0	0	0	0	0	u_4,6	0	u_4,8	0	0	0	0	0	0
	5	0	0	0	0	0	u_5,6	0	0	u_5,9	0	0	0	0	0
	6	0	0	0	0	0	0	u_6,7	u_6,8	u_6,9	u_6,10	0	0	0	0
S¹=	7	0	0	0	0	0	0	0	0	u_7,9	u_7,10	0	u_7,12	0	0
	8	0	0	0	0	0	0	0	0	0	u_8,10	0	0	0	0
	9	0	0	0	0	0	0	0	0	0	0	u_9,11	u_9,12	0	0
	10	0	0	0	0	0	0	0	0	0	0	0	u_10,12	u_10,13	0
	11	0	0	0	0	0	0	0	0	0	0	0	u_11,12	0	u_11,14
	12	0	0	0	0	0	0	0	0	0	0	0	0	u_12,13	u_12,14
	13	0	0	0	0	0	0	0	0	0	0	0	0	0	u_13,14
	14	0	0	0	0	0	0	0	0	0	0	0	0	0	0