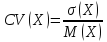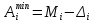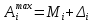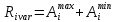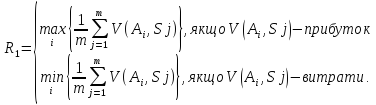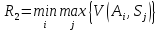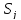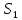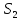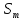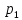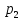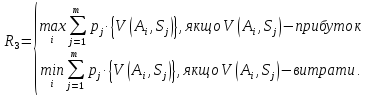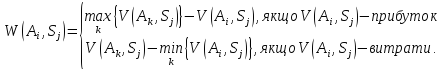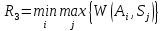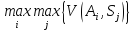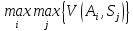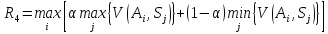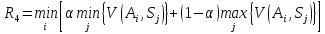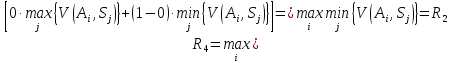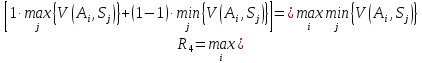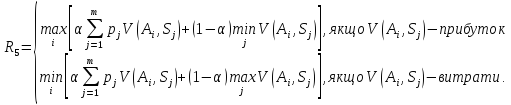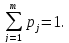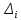ЗМІСТ
ВСТУП……………………………………………………………………………..3
ЗАВДАННЯ 1……………………………………………………………………...6
ЗАВДАННЯ 2…………………………………………………………………….31
ЗАВДАННЯ 3…………………………………………………………………….42
ЗАВДАННЯ 4…………………………………………………………………….82
ЗАВДАННЯ 5…………………………………………………………………...126
ВИСНОВКИ…………………………………………………………………….156
ПЕРЕЛІК ПОСИЛАНЬ…………………………………………………………159
ВСТУП
Дослідження операцій як самостійна наукова дисципліна з’явилась в роки другої світової війни, коли для вирішення складних проблем логістики та проектування систем озброєння створювались команди практиків, що містили в собі спеціалістів із найрізноманітніших сфер: математики, інженерії, економіки, психології, соціології, фізики на інші. Ці фахівці аналізували та формували проблему в кількісних виразах, щоб знайти її оптимальне вирішення, але за відсутністю технічного обладнання задача була дуже важкою. З розвитком техніки та технологій вирішення проблем стало набагато легше, але через багатофакторний вплив на показники опанування моделями та методами вирішення задач остається складною ланкою прийняття рішень.
Розквіт застосування математичних методів в економіці ознаменувало ХХ століття. Практично всіх вчених, що займались у той час дослідженням операцій відзначено Нобелівською премією. Спочатку це були найпростіші моделі, що обробляли статистичні економічні показники. Сьогодні методи, що вивчаються в межах дослідження операцій широко використовуються в операційному менеджменті та інших бізнес орієнтованих дисциплінах.
Дослідження операцій поєднує в собі сукупність методів та моделей, що дозволяють на базі економічної теорії, економічної статистики та математичного апарату приймати обґрунтовані управлінські рішення. Необхідність використання моделювання визначається тим, що багато об'єктів і пов'язані з ними проблеми дослідити безпосередньо або зовсім неможливо, або ж їхнє дослідження вимагає так багато сил і часу, що вже з цієї причини стає неможливим. Отже, побудова економетричних моделей дозволяє:
-
описати економічні процеси в кількісному виразі;
-
структурувати вхідні дані;
-
виділити зв’язок між досліджуваними показниками;
-
проаналізувати отриману модель;
-
отримати відповідні висновки, стосовно досліджуваної області;
-
надає можливість проведення прогнозування майбутнього стану показників.
Предметом дослідження операцій – є системи управління організацією чи окремим процесом, в якому етапи виконання є неузгодженими, або потребують оптимізації.
Об’єктом теорії дослідження операцій є організаційні системи або процеси. До таких відносять: фірми, підприємства, організаційні установи, відомства, установи матеріально-технічного постачання і торгівлі, міністерства, установи, що займаються проектуванням та плануванням.
Метою дослідження операцій – обґрунтування знайдених на основі досліджених моделей кількісних результатів та прийнятих управлінських рішень.
Маючи суттєве прикладне значення дослідження операцій вивчається багатьма вченими і в наш час, це обумовлено постійним процесом прийняття управлінських рішень різного роду та масштабу. Такі рішення впливають на роботу підприємства, відділу або людини, та мають велике економічне, соціальне або психологічне значення. Спираючись на суто математичний та інформаційний апарат, рішення, що приймаються, мають обґрунтований характер та є найоптимальнішими. До математичного та інформаційного апарату дисципліни відносять: системний аналіз, математичне програмування, теорію ігор, теорію оптимальних рішень, методи штучного інтелекту та інші.
Типовими класами задач дослідження операції є:
-
управління запасами. Вирішуються проблеми із затримкою виробництва, що викликана нестачею сировини, або навпаки із перенасиченням сировини чи інших матеріалів, що призводить до зайвих витрат на зберігання;
-
розподіл ресурсів. Ефективний розподіл ресурсів збільшує ефективність роботи підприємства чи установи, що призводить до збільшення прибутку як цілі організації;
-
моделі мережевого планування. Вирішення таких задач дозволяє раціонально використовувати обмежені ресурси та максимізувати прибуток, якщо задача стосується знаходження максимального, мінімального шляху, або всіх можливих шляхів;
-
задачі з нечіткими множинами. Методи що застосовуються дозволяють аналізувати показники, які не мають кількісного виразу та на основі лінгвістичних змінних будувати моделі для прийняття обґрунтованих рішень.
Завдання 1
Оцінити ефективність і ризикованість господарських рішень підприємця.
Розв’язання
Постановка завдання. Підприємець планує підвищити ефективність своєї діяльності, попередньо розробивши 5 стратегій А1, А2, А3, А4, А5.
Кожна з альтернативних стратегій розрахована відповідно до 6-ти станів зовнішнього середовища (С1, С2, …, С6).
Кожна стратегія відповідно до стану зовнішнього середовища оцінюється прибутками, який вважається випадковою величиною.
Таблиця 1.1 – Матриця альтернативних стратегій та прибутків
|
|
С1 |
С2 |
С3 |
С4 |
С5 |
С6 |
|
А1 |
6 |
18 |
22 |
9 |
21 |
23 |
|
А2 |
19 |
21 |
22 |
19 |
19 |
16 |
|
А3 |
21 |
18 |
11 |
19 |
10 |
16 |
|
А4 |
16 |
27 |
20 |
22 |
16 |
15 |
|
А5 |
16 |
12 |
18 |
8 |
17 |
10 |
Необхідно кількісно оцінити ризики кожної стратегії, застосувати статистичні критерії та вибрати найбільш ефективну стратегію розвитку.
Оцінку ризиків проведемо за наступними показниками:
-
математичне сподівання і середнє значення;
-
загальної дисперсії, додатної семіваріації, від’ємної семіваріації;
-
за стандартним відхиленням додатної та від’ємної семіваріації;
-
за показниками варіації;
-
за розмахом і графічним зображенням.
Математичне сподівання – значення економічного показника, обумовленого невизначеністю ситуації, зазвичай визначається як середньозважене за ймовірністю всіх можливих його значень, де ймовірність кожного значення використовується як питома вага, або статистична частота.
Математичне сподівання обчислюється за наступною формулою:
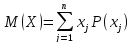 (1.1)
(1.1)
де M(X) – математичне сподівання випадкової (дискретної) величини;
Х – випадкова величина (ціна дохід, прибуток тощо);
xj – значення випадкової величини в окремому випадку, тобто на певному сегменті ринку реалізації конкретного товару або стосовно різних підприємств тощо;
 – ймовірність
випадкової величини;
– ймовірність
випадкової величини;
n – загальна кількість спостережень випадкової величини.
В досліджуваній ситуації, випадковою величиною буде прибуток. Математичне сподівання характеризуватиме середнє значення прибутку з врахуванням ймовірностей станів зовнішнього середовища. Чим більшою буде величина математичного сподівання, тим ефективнішою буде відповідна стратегія. Розрахунки наведено на рисунку 1.1.
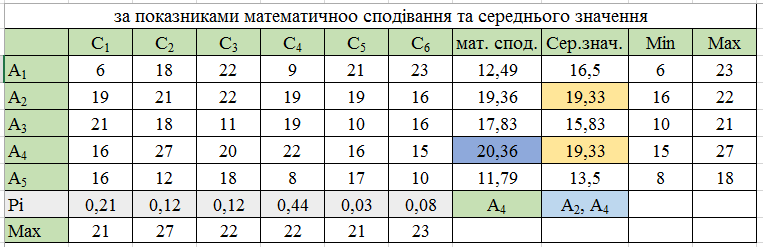
Рисунок 1.1 – оцінка ризиків стратегій за показниками математичного сподівання та середнього значення
Згідно математичного сподівання, стратегія А4 є найефективнішою. Також, розглядаючи середнє значення, можна проаналізувати оцінки ризиків стратегій. Чим більше середнє значення – тим вигіднішою є стратегія. З рисунку 1.1, випливає, що стратегія А2, та А4 мають найвигідніший характер за даним критерієм.
Проведемо оцінку ризиків стратегій за показниками дисперсії.
Дисперсія є мірою відхилення значень випадкової величини від центру розподілу. Більші значення дисперсії свідчать про більші відхилення значень випадкової величини від центру розподілу. Дисперсією випадкової величини, називається математичне сподівання квадрата відхилення цієї величини від її математичного сподівання (середнього значення).
Дисперсія дискретної випадкової величини Х має такий вигляд:
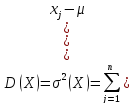 (1.2)
(1.2)
де D(X) – дисперсія випадкової (дискретної) величини;
 – стандартне
відхилення величини Х від її середнього
значення
– стандартне
відхилення величини Х від її середнього
значення
 ;
;
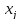 – значення
випадкової величини в окремому випадку,
тобто на певному сегменті ринку реалізації
конкретного товару або стосовно різних
підприємств тощо;
– значення
випадкової величини в окремому випадку,
тобто на певному сегменті ринку реалізації
конкретного товару або стосовно різних
підприємств тощо;
 – ймовірність
випадкової величини;
– ймовірність
випадкової величини;
n – загальна кількість спостережень випадкової величини.
Стандартне
відхилення або середнє квадратичне
відхилення, позначається як S або
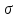 – у теорії ймовірності та статистиці
найбільш поширений показник розсіювання
значень випадкової величини відносно
іі математичного сподівання. Вимірюється
в одиницях виміру самої випадкової
величини.
– у теорії ймовірності та статистиці
найбільш поширений показник розсіювання
значень випадкової величини відносно
іі математичного сподівання. Вимірюється
в одиницях виміру самої випадкової
величини.
Стандартне
відхилення найбільш використовуваний
індикатор мінливості об’єкта, що
показує, на скільки в середньому
відхиляться індивідуальні значення
ознаки
 від їх середньої величини
від їх середньої величини
 .
.
Стандартне відхилення використовують під час розрахунку стандартної похибки середнього арифметичного, для побудови довірчих інтервалів, статистичної перевірки гіпотез, виміру лінійного взаємозв’язку між випадковими величинами.
Середньоквадратичне відхилення – дорівнює кореню квадратному з дисперсії випадкової величини:
 (1.3)
(1.3)
де Х – випадкова величина;
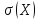 – стандартне
відхилення величини Х від її середнього
значення
– стандартне
відхилення величини Х від її середнього
значення
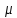
 – дисперсія
випадкової (дискретної) величини.
– дисперсія
випадкової (дискретної) величини.
Відповідно до формул з обчислення дисперсії
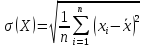 (1.4)
(1.4)
де Х – випадкова величина;
 – стандартне
відхилення величини Х від її середнього
значення
– стандартне
відхилення величини Х від її середнього
значення
 ;
;
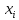 – значення
випадкової величини в окремому випадку;
– значення
випадкової величини в окремому випадку;
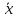 – середнє
арифметичне вибірки;
– середнє
арифметичне вибірки;
n – загальна кількість спостережень випадкової величини.

Рисунок 1.2 – Оцінка ризиків стратегій за показниками дисперсії, середньоквадратичного відхилення та варіації
Чим більшими є значення дисперсії та середньоквадратичного відхилення, тим більшим є ризик котрим володіє відповідна стратегія.
За результатами проведеного аналізу (рисунок 1.2), отримали що стратегія А2 володіє найменшим ризиком серед набору запропонованих.
Семіваріація (половинчаста дисперсія) є важливим показником оцінки ризику. Розрізняють додатну та від’ємну семіваріацію. Проведемо оцінку ризиків стратегій за показниками додатної та від’ємної семіваріації.
Додатна
семіваріація (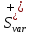 )
характеризує середній квадрат відхилень
тих значень прибутку, які більші від
середнього. Розраховується додатна
семіваріація за формулою:
)
характеризує середній квадрат відхилень
тих значень прибутку, які більші від
середнього. Розраховується додатна
семіваріація за формулою:
 (1.5)
(1.5)
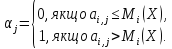 (1.6)
(1.6)
де
 – параметр вибору значень прибутку для
j-х
ринкових умов, які більші від середнього;
– параметр вибору значень прибутку для
j-х
ринкових умов, які більші від середнього;
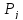 – суб’єктивна
ймовірність в ринкових умовах;
– суб’єктивна
ймовірність в ринкових умовах;
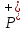 – сума
суб’єктивних ймовірностей для ринкових
умов, за яких рівень прибутку більший
від середнього.
– сума
суб’єктивних ймовірностей для ринкових
умов, за яких рівень прибутку більший
від середнього.
Додатна семіваріація – це дисперсія лише тих значень прибутку, які більші від середнього. Тобто чим більше значення додатної семіваріації, тим більшим є очікуваний від стратегії прибуток.

Рисунок 1.3 – Оцінка ризиків стратегій за показниками додатної семі варіації
За показниками додатної семіваріації найбільш вигідною є стратегія А1.
Від’ємна
семіваріація (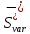 )
характеризує середні квадратичні
відхилення тих значень прибутку, які
менші за середнє. Тобто чим менша
)
характеризує середні квадратичні
відхилення тих значень прибутку, які
менші за середнє. Тобто чим менша
 ,
тим менші очікувані втрати.
,
тим менші очікувані втрати.
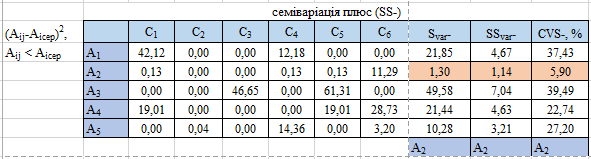
Рисунок 1.4 – Оцінка ризиків стратегій за показниками від’ємної семіваріації
За показниками від’ємної семіваріації найбільш вигідною є стратегія А2.
Проведемо оцінку ризиків стратегій за показниками семіквадратичних відхилень.
Додатні семіквадратичні відхилення характеризують лінійні відхилення від середнього значення тих рівнів прибутку, які більші від цього середнього. В нашому випадку – відхилення абсолютного значення очікуваного прибутку (можливе збільшення прибутку). Чим більшим є значення додатного семіквадратичного відхилення, тим більшим може виявитись абсолютне значення фактичного очікуваного прибутку. Згідно рисунку 1.3, за даним показником, кращою є стратегія А1.
Від’ємні семіквадратичні відхилення характеризують лінійні відхилення від середнього значення тих рівнів прибутку, які менші від цього середнього. В нашому випадку – відхилення абсолютного значення очікуваних втрат (можливе збільшення втрат). Більше значення від’ємного семіквадратичного відхилення, вказує на можливість збільшення абсолютного значення очікуваних втрат. Згідно рисунку 1.4, за даним показником, переважаючою є стратегія стратегія А2.
Проведемо оцінку ризиків стратегій за показниками варіації.
Варіація – розходження значень якої-небудь ознаки у різних одиниць сукупності за один і той же проміжок часу. Причиною виникнення варіації є різні умови існування різних одиниць сукупності. Варіація – необхідна умова існування і розвитку масових явищ. Визначення варіації необхідно при організації вибіркового спостереження, статистичному моделюванні і плануванні експертних опитувань. За ступенем варіації можна судити про однорідність сукупності, стійкість значень ознаки, типовість середньої, про взаємозв’язок між якими-небудь ознаками.
Відносним показником ризикованості є коефіцієнт варіації, який обчислюється за формулою:
|
|
(1.7) |
де 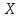 –
випадкова величина;
–
випадкова величина;
 – коефіцієнт
варіації випадкової величини
– коефіцієнт
варіації випадкової величини
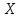 ;
;
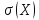 – стандартне
відхилення величини
– стандартне
відхилення величини
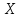 від її середнього значення
від її середнього значення
 ;
;
 – математичне
сподівання випадкової величини
– математичне
сподівання випадкової величини
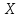 .
.
В нашому випадку, чим меншою є варіація прибутку, тим менш ризикованою є відповідна стратегія.
Найменше значення коефіцієнта варіації свідчить про найкраще співвідношення між ефективністю та ризиком.
Згідно результатів обчислення коефіцієнтів варіації на рисунках 1.2-1.4 отримали наступні комбінації оптимальних альтернатив:
-
за коефіцієнтом варіації СV – альтернатива A2;
-
за коефіцієнтом варіації CVS+ – альтернатива A1;
-
за коефіцієнтом варіації CVS- – альтернатива A2.
Коефіцієнт ризику показує, у скільки разів можливі середні втрати можуть перевищити можливі додаткові прибутки. Чим менший коефіцієнт ризику, тим менші ризики і в стратегії. Коефіцієнт ризику розраховується за формулою:
|
|
(1.8) |
Результат оцінки коефіцієнтів ризику різних альтернатив представлений на рисунку 1.5:

Рисунок 1.5 – Оцінка коефіцієнтів ризику
За значеннями коефіцієнтів ризику, найбільш вигідною є стратегія А2.
Гранична похибка розраховується для інтервальної оцінки ефективності рішення:
|
|
(1.9) |
де
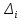 –
гранична похибка ефективності i-тої
стратегії;
–
гранична похибка ефективності i-тої
стратегії;
 – середня
стандартна похибка ефективності (ризик)
i-тої
стратегії;
– середня
стандартна похибка ефективності (ризик)
i-тої
стратегії;
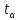 – табличне
значення t-критерію при рівні значущості
– табличне
значення t-критерію при рівні значущості
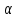 .
.
Рівень
значущості ( )
– це ймовірність, з якою інвестор
відхилятиме рівень граничної похибки,
а
)
– це ймовірність, з якою інвестор
відхилятиме рівень граничної похибки,
а
 – ймовірність, з якою інвестор
стверджуватиме рівень граничної похибки.
Наприклад, якщо
– ймовірність, з якою інвестор
стверджуватиме рівень граничної похибки.
Наприклад, якщо
 ,
то це означає, що з даною ймовірністю
інвестор відхиляє рівень граничної
похибки,
,
то це означає, що з даною ймовірністю
інвестор відхиляє рівень граничної
похибки,
 ймовірність,
з якою інвестор стверджує рівень
граничної похибки.
ймовірність,
з якою інвестор стверджує рівень
граничної похибки.
Гранична похибка теж належить до абсолютних показників оцінки ризику. Вона свідчить, як гранично із заданою ймовірністю може змінюватись ефективність кожної стратегії, тобто характеризує граничні відхилення від запланованої.
Чим більший рівень граничної похибки, тим більший ризик має стратегія за цим показником, і навпаки, чим менший рівень граничної похибки, тим менший ризик має стратегія.
В
нашому випадку табличне значення
критерію Стьюдента з рівнем довіри
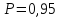 і кількістю ступенів свободи
і кількістю ступенів свободи
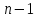 (6 – 1 = 5) рівне
(6 – 1 = 5) рівне
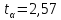 .
.
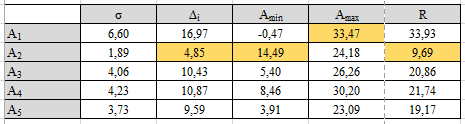
Рисунок 1.6 – Оцінка показників варіації
Додавши та віднявши граничну похибку до середнього значення прибутку отримаємо граничні межі, в яких буде коливатися фактичний прибуток по кожній стратегії (границі зміни ефективності).
Віднявши граничну похибку від величини середньої ефективності, визначимо мінімальний прибуток, який може отримати інвестор.
|
|
(1.10) |
де
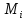 –
середня ефективність i-тої
стратегії;
–
середня ефективність i-тої
стратегії;
 – середня
стандартна похибка ефективності (ризик)
i-тої
стратегії.
– середня
стандартна похибка ефективності (ризик)
i-тої
стратегії.
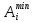 характеризує
мінімальне значення інтервалу
ефективності, виходячи з цього вигіднішою
є стратегія A2,
так як вона є не збитковою і має найбільше
додатне значення.
характеризує
мінімальне значення інтервалу
ефективності, виходячи з цього вигіднішою
є стратегія A2,
так як вона є не збитковою і має найбільше
додатне значення.
Сума середньої ефективності й граничної похибки покаже, який максимальний прибуток може отримати інвестор, реалізувавши рішення:
|
|
(1.11) |
де
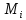 –
середня ефективність i-тої
стратегії;
–
середня ефективність i-тої
стратегії;
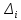 – середня
стандартна похибка ефективності (ризик)
i-тої
стратегії.
– середня
стандартна похибка ефективності (ризик)
i-тої
стратегії.
 характеризує
максимальну границю інтервалу
ефективності, за даним критерієм, кращою
є стратегія A1.
характеризує
максимальну границю інтервалу
ефективності, за даним критерієм, кращою
є стратегія A1.
Розмах варіації визначається як різниця між максимально і мінімально можливим прибутком.
|
|
(1.12) |
Розмах варіації визначається як довжина відрізка, на якому кожна точка може бути фактичним результатом рішення. Чим більший розмах варіації, тим більший ризик. Відповідно до даного критерію, найменш ризикованою буде стратегія – А2.
Для того, щоб простежити динаміку стратегій зобразимо графічно останні показники.

Рисунок 1.7 – Графік варіації розмаху альтернативних стратегій

Рисунок 1.8 – Графік варіації розмаху коефіцієнта ризику альтернативних стратегій

Рисунок 1.9 – Графік варіації Amin альтернативних стратегій
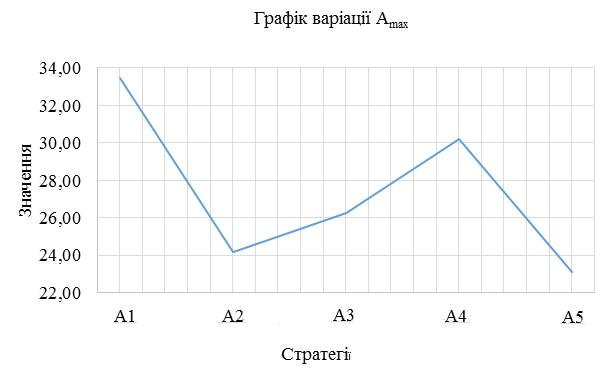
Рисунок 1.10 – Графік варіації Amax альтернативних стратегій

Рисунок 1.11 – Порівняльний графік варіації Amin та Amax
альтернативних стратегій
Проведемо оцінку ризиків стратегій за критерієм Лапласа. Критерій Лапласа використовується при умові, коли ймовірності можливих станів систем невідомі, тобто в умовах повної невизначеності. Даний критерій базується на використанні принципу недостатнього обґрунтування, який стверджує, що стани системи S1, S2, … , Sm мають рівні ймовірності.
Критерій Лапласа дає змогу відокремити кращу стратегію в тому випадку, якщо жодна з зовнішньоекономічних умов не має істотної переваги. Тому цей критерій не є вирішальним для вибору кращої стратегії, а лише додає більшої точності розрахункам.
Враховуючи вище сказане, початкову задачу можна розглядати як задачу прийняття рішень в умовах ризику, коли вибирається альтернатива Aі, яка дає найбільш очікуваний виграш R1 (коли V(Ai,Sj) моделює прибуток) або найменший очікуваний програш R1 (коли V(Ai,Sj) моделює витрати).
Отже, для знаходження величини R1має місце:
|
|
(1.12) |
|
|
|
де  – ймовірність реалізації стану
– ймовірність реалізації стану
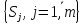 .
.
Даний критерій доцільно використовувати в тих випадках, коли різниця між окремими станами системи велика, тобто велика дисперсія значень.
|
критерій Лапласа |
|
|
Найкраща альтернатива |
19,33 |
|
А2,А4 |
|
Рисунок 1.12 – Результат обчислення значення критерію Лапласа
Виходячи з рисунку 1.12, найприбутковішими можуть бути стратегії А2 і А4, так як значення критерію Лапласа для них є найбільші.
Проведемо оцінку ризиків стратегій за критерієм Вальда. Даний критерій був запропонований Абрахамом Вальдо в 1955 році для вибірок рівного об’єму, а потім поширився на випадок вибірок різних обсягів. Критерій Вальда є найбільш обережним, оскільки він ґрунтується на виборі альтернативи з усіх найгірш можливих. У зв’язку з цим критерій Вальда часто називають максиміним (мінімаксним).
Якщо
результат V(Ai,
Sj)
відображає втрати особи, що приймає
рішення, то для альтернативи Ai
найбільші втрати, незалежно від можливого
стану Sj, будуть рівними
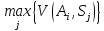 .
Відповідно до мінімаксного критерію
найкращою вибирається альтернатива
Ai,
яка дає:
.
Відповідно до мінімаксного критерію
найкращою вибирається альтернатива
Ai,
яка дає:
|
|
(1.13) |
Аналогічно в тому випадку, коли V(Ai, Sj) відображає виграш, відповідно до максиміного критерію, вибирається альтернатива Ai, яка дає:
|
|
(1.14) |
Застосування критерію Вальда виправдано, якщо ситуація, в якій приймається рішення наступна:
-
про можливість появи зовнішніх станів
 нічого не відомо;
нічого не відомо; -
доводиться рахуватися з появою різних зовнішніх станів
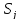 ;
; -
рішення реалізується тільки один раз;
-
необхідно виключити будь-який ризик.
В нашому випадку критерій Вальда розраховується для матриці виграшів (прибутків):
|
Критерій Вальда |
|
|
Найкраща альтернатива |
16,00 |
|
А2 |
|
Рисунок 1.13 – Результат обчислення значення критерію Вальда
Виходячи з рисунку 1.13, найприбутковою може бути стратегія А2, так як значення критерію Вальда для неї є найбільшим.
Проведемо
оцінку ризиків стратегій за критерієм
Байєса (максимум середнього виграшу).
Даний критерій використовується за
умови, коли відомий розподіл ймовірностей
настання станів системи. Припустимо,
що нам відомі значення ймовірностей
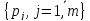 настання станів системи
настання станів системи
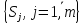 ,
які задаються наступним розподілом:
,
які задаються наступним розподілом:
Таблиця 1.2 – Розподіл ймовірностей настання станів системи
|
|
|
|
… |
|
|
|
|
|
|
… |
|
Існування закону розподілу ймовірностей станів системи надає можливість визначити математичне сподівання корисності при виборі кожної альтернативи. Оптимальною вважається та альтернатива, яка забезпечує екстремальне (min або max) значення даного математичного сподівання:
|
|
(1.15) |
Чим більшим є значення критерію Байєса, тим ефективнішою є стратегія. За даним критерієм, кращою є стратегія А4:
|
Критерій Байєса |
|
|
Найкраща альтернатива |
20,36 |
|
А4 |
|
Рисунок 1.14 – Результат обчислення значення критерію Байєса
Проведемо оцінку ризиків стратегій за критерієм Севіджа. Даний критерій ґрунтується на принципі мінімакса наслідків прийнятого помилкового рішення і намагається мінімізувати втрачену вигоду. Його зміст полягає у формуванні нової матриці втрат W(Ai, Sj) за допомогою наступної формули:
|
|
(1.16) |
Отримані значення показують величину ризику, тому критерій Севіджа називають критерієм мінімального ризику. У першому випадку W(Ai, Sj) є різницею найкращого значення в стовпці Sj і значенням V(Ai, Sj). За змістом, W(Ai, Sj) виражає «співчуття» особі, що приймала рішення, в зв’язку з тим, що вона не вибрала найкращої дії відносно стану Sj.
У другому випадку W(Ai, Sj) відображає різницю V(Ai, Sj) та найгіршого значення в стовпці Sj.
Незалежно від того, є V(Ai, Sj) прибутком або втратами, функція W(Ai, Sj), в обох випадках визначає втрати. Тому до W(Ai, Sj) слід використовувати тільки мінімаксний критерій.
Суть даного підходу в тому, щоб уникати великого ризику при прийнятті рішення. У сенсі «песимізму» критерій Севіджа схожий на критерій Вальда, але сам «песимізм» в даному випадку має дещо інакший зміст.
Вимоги, що пред’являються до ситуації, в якій приймається рішення, збігаються з вимогами до критерію Вальда.
Отже, формула для вибору оптимальної альтернативи з допомогою критерія мінімального ризику набуває вигляду:
|
|
(1.17) |
Критерій Севіджа розраховується для матриці ризиків (втрат), тому його менше значення вказує на перевагу певної стратегії. За даним критерієм, кращою є стратегія А2:
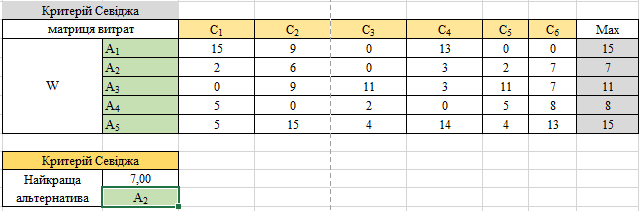
Рисунок 1.15 – Результат обчислення значення критерію Севіджа
Розглянутий критерій досить часто використовується в практичній діяльності при прийнятті управлінських рішень на тривалий період. Наприклад: при розподілі капітальних вкладень на перспективу він дає добрі результати.
Проведемо оцінку ризиків стратегій за критерієм Гурвіца. Намагаючись зайняти найбільш врівноважену позицію, Гурвіц запропонував оцінювальну функцію, яка знаходиться між точкою зору крайнього оптимізму та крайнього песимізму.
При найбільш оптимістичному підході можна вибрати альтернативу:
|
|
(1.18) |
де V(Ai, Sj) являє собою виграш (прибуток).
Аналогічно для найбільш песимістичних припущень вибрана альтернатива відповідає:
|
|
(1.19) |
Критерій
Гурвіца встановлює баланс між випадками
крайнього оптимізму й крайнього
песимізму, порівнюючи обидві альтернативи
з допомогою відповідних коефіцієнтів
 ,
та
,
та
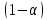 ,
де
,
де
 .
Якщо
.
Якщо
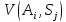 ,
представляє прибуток, то вибираємо
альтернативу:
,
представляє прибуток, то вибираємо
альтернативу:
|
|
(1.20) |
У
випадку, коли
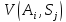 представляє втрати, критерій вибирає
альтернативу:
представляє втрати, критерій вибирає
альтернативу:
|
|
(1.21) |
Параметр
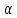 являє собою показник оптимізму (ступінь
впевненості): при
являє собою показник оптимізму (ступінь
впевненості): при
 ,
критерій крайного оптимізму; при
,
критерій крайного оптимізму; при
 – крайнього песимізму.
– крайнього песимізму.
У
технічних додатках складно вибрати
ваговий множник
 ,
тому що важко знайти кількісну
характеристику для тих часток оптимізму
і песимізму, які присутні при прийнятті
рішення. Тому найчастіше
,
тому що важко знайти кількісну
характеристику для тих часток оптимізму
і песимізму, які присутні при прийнятті
рішення. Тому найчастіше
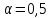 .
.
Значення
 (
(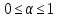 )
може визначитися в залежності від
характеру особи, яка приймає рішення,
тобто, що їй більш характерно: песимізм
чи оптимізм. Чим складніша ситуація,
чим більше в ній хоче підстрахуватись
ОПР, тим ближче до нуля вибирається
)
може визначитися в залежності від
характеру особи, яка приймає рішення,
тобто, що їй більш характерно: песимізм
чи оптимізм. Чим складніша ситуація,
чим більше в ній хоче підстрахуватись
ОПР, тим ближче до нуля вибирається
 .
Якщо
.
Якщо
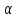 наближається до нуля, то збільшується
невпевненість при досягненні успіху.
Використання даного критерію ускладнюється
при відсутності достатньої інформації
про величину параметра
наближається до нуля, то збільшується
невпевненість при досягненні успіху.
Використання даного критерію ускладнюється
при відсутності достатньої інформації
про величину параметра
 ,
який в силу суб’єктивних причин при
різних рішеннях і в різних ситуаціях
приймає різні значення. При відсутності
інформації про явно виражений характер
особи
,
який в силу суб’єктивних причин при
різних рішеннях і в різних ситуаціях
приймає різні значення. При відсутності
інформації про явно виражений характер
особи
 приймається рівним 0,5.
приймається рівним 0,5.
Припустимо,
що
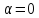 ,
тобто ОПР має мало надії на сприятливий
наслідок, тоді отримаємо:
,
тобто ОПР має мало надії на сприятливий
наслідок, тоді отримаємо:
|
|
(1.22) |
При
абсолютній впевненості в досягненні
успіху (значення
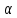 приймаємо рівним 1), отримуємо крайній
оптимізм:
приймаємо рівним 1), отримуємо крайній
оптимізм:
|
|
(1.23) |
За
умови, що ОПР не має змоги визначити
коефіцієнт
 ,
а компроміс між оптимістичним і
песимістичним рішенням бажаний
використовуємо вираз:
,
а компроміс між оптимістичним і
песимістичним рішенням бажаний
використовуємо вираз:
|
|
(1.24) |
Критерій Гурвіца застосовується у разі, коли:
-
про ймовірності появи стану
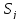 нічого не відомо;
нічого не відомо; -
з появою стану
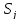 необхідно рахуватися;
необхідно рахуватися; -
реалізується тільки мала кількість рішень;
-
допускається певний ризик.
Результат обчислень критерію Гурвіца представлений на рисунку 1.16:
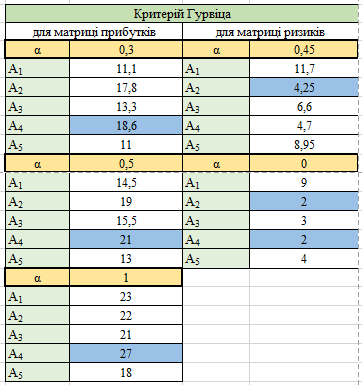
Рисунок 1.16 – Результат обчислення значень критерію Гурвіца
За даним критерієм, вигіднішими виявилися стратегії:
-
для матриці прибутків: А4, A4, A4;
-
для матриці ризиків: А2, A2 та А4.
Проведемо
оцінку ризиків стратегій за критерієм
Ходжеса-Лемана. Даний критерій використовує
два суб’єктивних показники: закон
розподілу ймовірностей
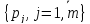 настання станів системи
настання станів системи
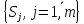 і параметр оптимізму
і параметр оптимізму
 для критерію Гурвіца.
для критерію Гурвіца.
Для загального випадку критерій Ходжеса-Лемана визначається виразом:
|
|
(1.25) |
|
|
де
|
|
|
Результат обчислень критерію Ходжеса-Лемана для альтернативних стратегій представлений на рисункук 1.17:

Рисунок 1.17 – Результат обчислення значень критерію Ходжеса-Лемана
Для матриці прибутку: чим більше значення даного критерію, тим більше можливе значення очікуваного прибутку, значить за цим показником кращими є стратегії – А2, А2, А4, А4.
Для матриці ризиків: критерій характеризує очікувані втрати, а отже чим менше значення, тим кращими є стратегії – А4, А2.
Побудуємо зведену таблицю показників і критеріїв.
Таблиця 1.3 – Таблиця кращих альтернатив за показниками та критеріями
|
|
Назва |
Краща альтернатива |
Напрям |
|
Показники |
Мат. спод. |
А4 |
max |
|
Сер. знач |
А2, А4 |
max |
|
|
Di |
A2 |
min |
|
|
Svar+ |
A1 |
max |
|
|
Svar- |
A2 |
min |
|
|
SSvar+ |
A1 |
max |
Продовження таблиці 1.3
|
|
Назва |
Краща альтернатива |
Напрям |
|
|
SSvar- |
A2 |
min |
|
|
CV |
A2 |
min |
|
CVS+ |
A1 |
max |
|
|
CVS- |
A2 |
min |
|
|
σ |
A2 |
min |
|
|
|
A2 |
min |
|
|
Amax |
A1 |
max |
|
|
Amin |
A2 |
max |
|
|
R |
A2 |
min |
|
|
K |
A2 |
min |
|
|
Критерії |
Лапласа |
А2, А4 |
– |
|
Вальда |
А2 |
– |
|
|
Байєса |
А4 |
– |
|
|
Севіджа |
А2 |
– |
|
|
Гурвіца |
А4, А4, А4 А2, А2, А4 |
– |
|
|
Ходжеса-Лемана |
А2, А2, А4, А4 А4, А2 |
– |
Таблиця 1.4 – Таблиця статистики вибору кращих альтернатив
|
Стратегія |
Кількість разів, коли стратегія була оптимальною |
|
А1 |
4 |
|
А2 |
18 |
|
А3 |
0 |
|
А4 |
11 |
|
А5 |
0 |
Висновки: оскільки стратегія А2 була обрана оптимальною найбільшу кількість разів (18) за різноманітними показниками та критеріями, то вона є найефективнішою. Стратегія А2 приноситиме найбільший середній прибуток в розмірі – 19,33. Всі показники варіації не є високими, відповідно стратегія є також мало ризикованою.
Варто відмітити, що стратегія А4 була обрана 11 разів, що також свідчить про її ефективність та приділенні їй належної уваги. Стратегії А3 та А5 жодного разу не були обрані, а отже є зовсім неефективними.