Вывод остатков Таблица 5

ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Ct	Остатки
1	266888,6731	-2783,67
2	268952,7931	9432,207
3	256283,171	-7731,17
4	258023,645	3839,355
5	251041,709	-1982,71
6	246347,673	-3242,67
7	240593,855	-6615,85
8	241287,239	2866,761
9	237641,295	3696,705
10	228826,701	-5779,7
11	226595,247	-2129,25
12	222977,359	-1243,36
13	223599,267	8096,733
14	219978,373	3576,627

В рассматриваемой задаче:

^׀= 145277,6

^׀= 0,334

С помощью уже определенных значений ^׀и ^׀находим сами значения величин и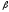по формулам: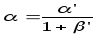

Получаем, что:

= 108903,8

= 0,250375

Следовательно, уравнение функции потребления (1) примет вид:

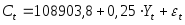
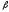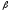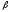Далее сравниваем значения и, найденные по формулам, с табличными значениямии(_табл. = 150000, _табл. = 0,32), и находим проценты несовпадения данных величин, используя для этого формулы:

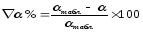
Получаем, что процент ошибки для величины равен -27,4 %, а для величины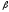 он равен -21,8 %.

1.2. Определение параметров уравнения регрессии с использованием мнк

Для определения параметров уравнения регрессии с помощью прямого МНК, необходимо определить величину Y_t для каждого t (t = 1…14) По формуле (2) определяем значения величин Y_t, используя значения C_t и I_t из таблицы №1 «Исходные данные». Полученные значения заносим в таблицу №6

Таблица 6

Значения величины Yt

t	Ct	It	Yt
t1	264105	100000	364105
t2	278385	91900	370285
t3	248552	83800	332352
t4	261863	75700	337563
t5	249059	67600	316659
t6	243105	59500	302605
t7	233978	51400	285378
t8	244154	43300	287454
t9	241338	35200	276538
t10	223047	27100	250147
t11	224466	19000	243466
t12	221734	10900	232634
t13	231696	2800	234496
t14	223555	100	223655

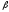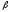Приняв в качестве исходных данных имеющиеся значения C_t и Y_t, с помощью МНК определяем смещённые оценки ^см и ^см величин и, используя уравнение (1). Для этого используем имеющиеся в табличном редактореExcel пакет прикладных программ, реализующий определение параметров уравнения регрессии методом наименьших квадратов. Активация этого метода осуществляется командами: «Сервис» - «Анализ данных» - «Регрессия».

Получаем следующие таблицы:

Таблица 7

Регрессионная статистика
Множественный R	0,889809
R-квадрат	0,791759
Нормированный R-квадрат	0,774406
Стандартная ошибка	8220,482
Наблюдения	14

Таблица 8

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	1	3,08E+09	3,08E+09	45,62565	2,03E-05
Остаток	12	8,11E+08	67576321
Итого	13	3,89E+09

Таблица 9

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение
Y-пересечение	219974	3941,029	55,81638	7,21E-16
It	0,462968	0,06854	6,754676	2,03E-05

Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
211387,2027	211387,2	228560,7	211387,2027
0,313631321	0,313631	0,612305	0,313631321

Таблица 10