ГОСДАРСТВЕННЫЙ ИНСТИТУТ ЭКОНОМИКИ, ФИНАНСОВ, ПРАВА И ТЕХНОЛОГИЙ

Кафедра информационных технологий и высшей математики

Дисциплина: эконометрика

ОТЧЕТ

о лабораторной работе № 3

на тему:

«Определение параметров уравнения регрессии косвенным методом наименьших квадратов»

кАФЕДРА ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ И ВЫСШЕЙ МАТЕМАТИКИ

дисциплина: «эконометрика»

вариант №13

Выполнила: Студентка 121 группы

Экономического факультета

III курса

Слепнева А.Р.

Проверил: Пучков В.Ф.

Гатчина

2014

Содержание

Введение…………………………………………………………………………3

1.Алгоритм решения…………………………………………………………….4

1.1 Определение параметров уравнения регрессии с помощью КМНК…...4

1.2 Определение параметров уравнения регрессии с помощью МНК……..8

1.3 Анализ значений показателей…………………………………………...11

2.Проверка адекватности модели…………………..………………………….12

3.Определение точности модели………………………………………………19

Заключение…………………………………………………………………...….25

Введение

Специфической особенностью деятельности экономиста является работа в условиях недостатка информации и неполноты исходных данных. Анализ такой информации требует специальных методов, которые составляют один из аспектов эконометрики.

Становление и развитие эконометрического метода происходили на основе так называемой высшей статистики - на методах парной и множественной регрессии, парной, частной и множественной корреляции, выделения тренда и других компонент временного ряда, на статистическом основании. Центральной проблемой эконометрики является построение эконометрической модели и определение возможностей её использования для описания, анализа и прогнозирования реальных экономических процессов.

Актуальность темы заключается в том, что в настоящее время, действительно важен вопрос о построении эконометрической модели и об определении возможностей ее использования для описания, анализа и прогнозирования реальных экономических процессов.

Цель работы - определение параметров уравнения регрессии косвенным методом наименьших квадратов.

Задачей данной работы является определение в простой кейнсианской модели формирования доходов параметров уравнения функции потребления.

Отчёт состоит из введения, 5 разделов ,заключения и списка литературы.

1.Алгоритм решения

1.1. Определение параметров уравнение регрессии с помощью кмнк

Исходная система уравнений имеет вид:

C_t = +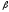Y_t + ε_t (1)

Y_t = C_t + I_t (2),

• C_t - функция потребления

• Y_t- функция дохода

• ε_t – случайная составляющая

• I_t – инвестиции.

Переменные Ct и Yt являются эндогенными. Эндогенной считается та переменная, значение которой определяется внутри уравнения регрессии, внутри модели. В качестве экзогенной переменной в данной задаче выступают инвестиции It. Экзогенной является та переменная, значение которой определяется вне уравнения регрессии, вне модели и поэтому берется как заданная (It).

Параметры уравнения регрессии необходимо определить двумя способами: косвенным методом наименьших квадратов и прямым методом наименьших квадратов.

Для этого введем исходные данные и представим таблицу исходных данных, как указано в методическом пособии:

Таблица 1

t	Ct	It
t1	264105	100000
t2	278385	91900
t3	248552	83800
t4	261863	75700
t5	249059	67600
t6	243105	59500
t7	233978	51400
t8	244154	43300
t9	241338	35200
t10	223047	27100
t11	224466	19000
t12	221734	10900
t13	231696	2800
t14	223555	100

Методом наименьших квадратов (МНК) из уравнения (1) найти параметры и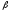невозможно, так как оценки будут смещёнными. Необходимо использовать косвенный метод наименьших квадратов (КМНК).

Для этого эндогенные переменные выражаем через экзогенные переменные.

Подставим уравнение (2) в уравнение (1):

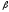C_t = +(C_t + I_t) + ε_t,

После некоторых преобразований имеем уравнение вида (3):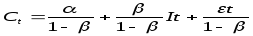

Данное уравнение не содержит в правой части эндогенных переменных, а имеет только экзогенную переменную в виде I_t. Экзогенная переменная не коррелирует со случайной составляющей и, следовательно, параметры этого уравнения могут быть найдены с помощью МНК.

Представим это уравнение в следующем виде:

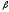C_t = ^׀+ ^׀I_t + ε_t^׀,

где: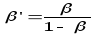

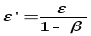
Далее, используя исходные значения величин C_t и I_t (таблица №1), с помощью МНК находим несмещённые оценки ^׀и ^׀.

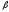Для этого используем имеющиеся в табличном редакторе Excel пакет прикладных программ, реализующий определение параметров уравнения регрессии методом наименьших квадратов. Активация этого метода осуществляется командами: «Сервис» - «Анализ данных» - «Регрессия». В диалоговом окне «Регрессия» в поле «Входной интервал Y» вводим данные соответствующие объему потребления(C_t), включая название реквизита. В поле «Входной интервал X» вводим данные по данным инвестиционного спроса (I_t). Затем устанавливаем флажки в окнах «Метки» и «Уровень надежности». Установим переключатель «Новый рабочий лист» и поставим галочки в окошках «Остатки». После всех вышеперечисленных действий нажимаем кнопку «ОК» в диалоговом окне «Регрессия». В результате выше перечисленных действий получаем значения коэффициентов регрессии, а также данные для анализа регрессионной модели:

Таблица 2

Регрессионная статистика
Множественный R	0,951420394
R-квадрат	0,905200766
Нормированный R-квадрат	0,89730083
Стандартная ошибка	5546,474009
Наблюдения	14

Таблица 3

Дисперсионный анализ
		df	SS	MS
Регрессия		1	3,52E+09	3524968936
Остаток		12	3,69E+08	30763373,93
Итого		13	3,89E+09
F	Значимость F
114,583301	1,71E-07

Таблица 4

		Коэффициенты			Стандартная ошибка		t-статистика
Y-пересечение		145277,6028			9163,41		15,85409852
Yt		0,334000001			0,031202		10,70435897
P-Значение	Нижние 95%		Верхние 95%	Нижние 95,0%		Верхние 95,0%
2,05983E-09	125312,2		165243	125312,2478		165242,9578
1,70832E-07	0,266016		0,401984	0,266016155		0,401983846