- •Лекція № 9 Тема: Випадкові величини і розподіли
- •1. Випадкові величини
- •2. Функція розподілу випадкової величини
- •3. Щільність розподілу
- •4. Числові характеристики розподілу випадкових величин
- •1) Характеристики положення а) Математичне сподівання випадкової величини
- •Властивості математичного сподівання
- •Б) Мода та медіана випадкової величини
- •2) Характеристики розсіювання: Дисперсія та середнє квадратичне відхилення
- •Властивості дисперсії
- •3) Характеристики форми Моменти розподілу випадкової величини. Коефіцієнти асиметрії та ексцесу.
2) Характеристики розсіювання: Дисперсія та середнє квадратичне відхилення
Різні випадкові величини можуть мати одне й те саме математичне сподівання, але істотно різний характер розподілу.
Тому необхідно ввести ще одну числову характеристику випадкової величини – для виміру ступеня розсіювання, розкиду значень випадкової величини навколо її математичного сподівання. Тому математичне сподівання називають ще центром розсіювання. Для вимірювання розсіювання вводиться числова характеристика, яку називають дисперсією.
Означення. Дисперсією випадкової величини Х називається математичне сподівання квадрата відхилення цієї випадкової величини від її математичного сподівання:
 (9)
(9)
Очевидно,
чим менше дисперсія випадкової величини
Х, тим краще значення випадкової величини
 описуються її математичним сподіванням.
описуються її математичним сподіванням.
На практиці для обчислення дисперсії застосовується так звана робоча формула:
 (10)
(10)
Для
дискретної випадкової величини
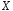
 (11)
(11)
Для неперервної випадкової величини
 . (12)
. (12)
Слід
пам’ятати, що дисперсія
не може бути від’ємною величиною
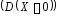 .
.
Властивості дисперсії
1. Дисперсія сталої величини дорівнює нулю:

Справді,
 .
.
2. Сталий множник можна виносити за знак дисперсії, підносячи до квадрату:
 .
.
Маємо:

 .
.
3. Якщо дві випадкові величини незалежні, то дисперсія їх суми або різниці дорівнює сумі дисперсій цих величин, тобто

Ця властивість виконується і для будь-якого скінченого числа випадкових величин.
Отже, дисперсія характеризує розсіювання випадкової величини відносно свого математичного сподівання. Якщо випадкова величина виміряна в деяких одиницях, то дисперсія вимірюватиметься в цих самих одиницях, але в квадраті.
Тому доцільно мати числову характеристику такої самої вимірності, як і випадкова величина. Такою числовою характеристикою є середнє квадратичне відхилення.
Означення. Середнім квадратичним відхиленням випадкової величини Х називається корінь квадратний з дисперсії:
 .
.
Приклад 9. Для дискретної випадкової величини з прикладу 1.
|
|
–4 |
–1 |
2 |
6 |
9 |
13 |
|
|
0,1 |
0,2 |
0,1 |
0,3 |
0,1 |
0,2 |
обчислити
 ,
, .
.
Розв’язання. За формулою (4) маємо:
 .
.
Знайдемо:
 .
.
 .
.
Тоді
 ;
;

Приклад 10 . Для неперервної випадкової величини з прикладу 2, заданої щільністю ймовірностей
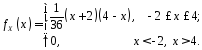
обчислити
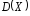 ,
, .
.
Розв’язання.
Знайдемо
 ;
;

 .
.
За формулою (4)
 ;
;

3) Характеристики форми Моменти розподілу випадкової величини. Коефіцієнти асиметрії та ексцесу.
Узагальненими числовими характеристиками випадкових величин є моменти розподілу. За невеликою кількістю моментів можна визначити характер розподілу. Поняття моментів впровадив у математику великий російський математик П.Л. Чебишов.
Означення.
Моментом k-го порядку
випадкової величини
 називають математичне сподівання k-го
степеня відхилення величини
називають математичне сподівання k-го
степеня відхилення величини від
деякої сталої величини
від
деякої сталої величини :
:
 . (13)
. (13)
В
залежності від значення величини
 моменти поділяються на початкові і
центральні.
моменти поділяються на початкові і
центральні.
Якщо
 ,
то моменти називаютьсяпочатковими
і
позначаються
,
то моменти називаютьсяпочатковими
і
позначаються
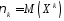 ,
,
Якщо
 – дискретна випадкова величина, то її
початкові моменти визначаються формулами
– дискретна випадкова величина, то її
початкові моменти визначаються формулами

Якщо
 – неперервна випадкова величина, то її
початкові моменти визначаються формулами
– неперервна випадкова величина, то її
початкові моменти визначаються формулами

З цих формул випливає, що
при
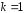
 ;
при
;
при
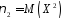 і т. д.
і т. д.
Якщо
 ,
то моменти називаютьсяцентральними
і
позначаються
,
то моменти називаютьсяцентральними
і
позначаються
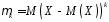 ,
,
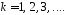
Якщо
 – дискретна випадкова величина, то її
центральні моменти будуть визначатися
формулами
– дискретна випадкова величина, то її
центральні моменти будуть визначатися
формулами

Якщо
 – неперервна випадкова величина, то її
центральні моменти будуть визначатися
формулами
– неперервна випадкова величина, то її
центральні моменти будуть визначатися
формулами

З цих формул випливає, що
при

 ;
;
при
 ;
;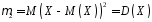 ;
;
при

 ;
;
при

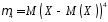 .
.
Для
симетричного розподілу (крива такого
розподілу симетрична відносно прямої
 кожний центральний момент непарного
порядку дорівнює нулю. Тому кожний
відмінний від нуля центральний момент
непарного порядку характеризує степінь
асиметрії розподілу.
кожний центральний момент непарного
порядку дорівнює нулю. Тому кожний
відмінний від нуля центральний момент
непарного порядку характеризує степінь
асиметрії розподілу.
Найпростішою
з таких характеристик є 3,
але для зручності замість цієї величини
беруть безрозмірну величину
 .
.
Якщо
випадкова величина
 має скінченні моменти до четвертого
включно, то величина
має скінченні моменти до четвертого
включно, то величина
 (14)
(14)
називається коефіцієнтом асиметрії.
Якщо
 ,
то розподіл має правосторонню асиметрію;
,
то розподіл має правосторонню асиметрію;
якщо
 ,
то розподіл має лівосторонню асиметрію;
,
то розподіл має лівосторонню асиметрію;
якщо
 ,
то розподіл симетричний.
,
то розподіл симетричний.
Величина
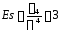 (15)
(15)
називається коефіцієнтом ексцесу її розподілу.
Якщо
 ,
то розподіл низьковершинний;
,
то розподіл низьковершинний;
якщо
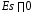 ,
то розподіл високовершинний;
,
то розподіл високовершинний;
якщо
 ,
то розподіл нормальний.
,
то розподіл нормальний.
Ці
величини характеризують ступінь
відмінності функції розподілу
 від функції розподілу
від функції розподілу стандартного нормального розподілу,
для якого
стандартного нормального розподілу,
для якого .
.
Приклад 11 Для дискретної випадкової величини з прикладу 1
|
|
–6 |
–4 |
2 |
4 |
6 |
8 |
|
|
0,1 |
0,1 |
0,2 |
0,3 |
0,1 |
0,2 |
обчислити
 ,
, .
.
Розв’язання.

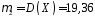 ,
,



 .
.
 .
.
Оскільки
 ,
то розподіл має правосторонню асиметрію;
,
то розподіл має правосторонню асиметрію;

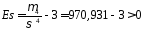 .
.
Оскільки
 ,
то розподіл високовершинний.
,
то розподіл високовершинний.
Приклад 12. Для неперервної випадкової величини з прикладу 2, заданої щільністю ймовірностей

обчислити
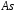 ,
, .
.
Розв’язання.
 ;
;
 ;
;
 .
.


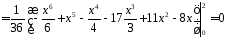 .
.
 .
.
Оскільки
 ,
то розподіл симетричний.
,
то розподіл симетричний.

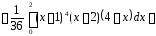
 .
.
 .
.
Оскільки
 ,
то розподіл низьковершинний.
,
то розподіл низьковершинний.