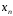2. Функція розподілу випадкової величини

Нехай – довільна випадкова величина, а– будь-яке її допустиме значення.

Означення. Функцією розподілу ймовірностей довільної випадкової величини або просто функцією розподілу величини називається функція, яка представляє розподілвеличини : значення цієї функції в точцідорівнює ймовірності того, що випадкова величинанабуває значення менше:

.

Оскільки функція розподілу являє собою ймовірність, вона повинна задовольняти основним аксіомам теорії ймовірностей і мати властивості, притаманні ймовірностям. Але ця функція залежить від можливих значень випадкової величини , і тому повинна в загальному вигляді визначатися для всіх значень. Таким чином, вимога, щоб функція розподілу являла собою ймовірність, накладає на її властивості певні обмеження.

Основні властивості функції розподілу довільної випадкової величини:

1) , ;

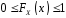2) ,(,)

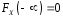3) Функція не зменшується при зростанні(неспадна, тобто, якщо.)

4) .

Відзначимо ще одну властивість функції :

5) Якщо , то

,

тобто стрибок функції в довільній точцізбігається з ймовірністю події.

Нехай – дискретна випадкова величина, задана таблицею розподілу:

			…		…
			…		…

Для довільного числа подіяє сума подій, тому ймовірність подіїє сума ймовірностей, тобто

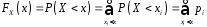
Отже, функція 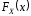є неперервною всюди, крім точок стрибків і є розривною у всіх точкахз величиною стрибка, залишаючись неперервною зліва в цих точках.

Графік функції являє собою східчасту ламану зі стрибками в точках,, …,... . Величини стрибків дорівнюють,,…,,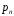 ... відповідно. Лівішеграфік збігається з віссю, правіше– із прямою.

Приклад 3. Побудувати функцію розподілу дискретної випадкової величиниз прикладу 1 та її графік.

Розв’язання. Згідно з означенням і властивостями , дістаємо співвідношення.

1) ;

2) ;

3) ;

4)

;

5)

;

6)

.

7)

.

Компактно можна записати в такій формі:

Графік функції зображено на малюнку:

Нехай – неперервна випадкова величина. Графік функціїявляє собою криву, обмежену віссюі прямою.

Між двома класами випадкових величин – дискретними і неперервними існують взаємовідношення, які полягають в тому, що будь-яку неперервну випадкову величину можна одержати граничним переходом з дискретних випадкових величин. Наочне уявлення про це дає графік функції розподілу дискретної випадкової величини. Якщо уявити собі, що до множини можливих значень випадкової величини додаються все нові точки, то кількість сходинок на кривійбуде ставати усе більше, а самі сходинки усе дрібніше. Східчаста ламана все більше буде наближатися до плавної кривої, а дискретна випадкова величина – до неперервної випадкової величини.

Приклад 4. Закон розподілу неперервної випадкової величини задано функцією розподілу ймовірностей

Побудувати графік функції і обчислити.

Розв’язання. графічно зображено на малюнку:

Обчислимо

.

3. Щільність розподілу

Хоч функція розподілу і дає вичерпний опис ймовірнісної моделі однієї випадкової величини, її форма не завжди зручна для виконання необхідних розрахунків.

Означення. Якщо існує така функція , що для довільних

,

то кажуть, що випадкова величина має щільність .

Коли щільність існує, її можна знайти диференціюванням функції розподілу:

Фізичний зміст щільності розкривається через елемент ймовірності , який можна записати у вигляді:

.

Це співвідношення стверджує, що є ймовірність того, що випадкова величина лежить в діапазоні можливих значень міжі.

Оскільки – це щільність ймовірності, а не сама ймовірність, вона не обов’язково має бути менше 1 і може набувати будь-яких невід'ємних значень.

Основні властивості щільності ймовірності:

1. , ;

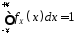2. (умова нормування);

3. ;

4. .

Графічно функція зображується кривою, що лежить у верхній півплощині і такою, що площа, укладена між нею й віссю, дорівнює 1:

Не будь-яка випадкова величина має щільність. Наприклад, її немає в дискретних випадкових величин.