Модуль 1

Тема 1. Фізичні основи механіки. Кінематика Лекція 1. Основи кінематики поступального та обертального рухів Основні визначення

В механіці розглядають механічний рух. Під механічним рухом розуміють зміну з часом положення тіла відносно інших тіл в просторі з часом. Тіло відліку– це тіло, відносно якого розглядається рух. Тіло відліку, система координат, пов’язана з ним і прилад для вимірювання часу разом становлятьсистему відліку. На практиці використовують декартову, циліндричну і сферичну системи координат.

Основна задача механіки – визначити положення тіла в будь-який момент часу в просторі. Для цього використовують певні фізичні величини та поняття. Матеріальна точка– це тіло, розмірами якого (але не масою!) за даних умов задачі можна знехтувати. Наприклад, у випадку переміщення автомобіля на відстань, яка набагато більша за розміри самого автомобіля, останній можна вважати матеріальною точкою, проте той самий автомобіль не можна приймати за матеріальну точку, коли в задачі розглядаються рухи в середині самого автомобіля, чи переміщення авто відбувається на відстані, співрозмірні чи менші за розміри транспортного засобу.

Т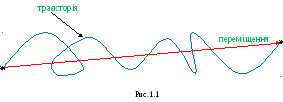раєкторія– це лінія, яку описує тіло під час свого руху (рис. 1.1).Шлях– це довжина траєкторії або це відстань, яку проходить тіло під час свого руху.Переміщення– це вектор, що сполучає початкове і кінцеве положення тіла.

Швидкість і прискорення

Нехай матеріальна точка рухається з т. А в т. В (рис. 1.2). Тоді- переміщення, довжина дуги АВ траєкторії між початковим і кінцевим положенням точки є шляхом. Різні тіла за один і той же проміжок часу можуть здійснювати різні переміщення.

Фізична величина:

(1.1)

називається середньою швидкістю.

Якщо зменшувати проміжок часу , то відношеннябуде прямувати до деякої границі. Границя, до якої прямує середня швидкість при умові, що проміжок часуназивається миттєвою швидкістю, або швидкістю в даний момент часу в даній точці траєкторії. За означенням:

(1.2)

Миттєва швидкістьє першою похідною від радіус-вектора по часу. Примодуль вектора переміщення можна вважати приблизно рівним довжині дуги траєкторії, в цьому випадку модуль вектора швидкості буде такий:

, (1.3)

де - це шлях, пройдений тілом за час. Фізична величина, яка визначається із співвідношення:

(1.4)

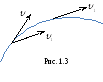називаєтьсясереднім прискореннямтіла на проміжку часу.

(1.5)

Якщо зменшувати проміжок часу , то привеличинабуде наближатись до деякої границі. Фізична величина, яка визначається із співвідношення:

(1.6)

називається прискореннямматеріальної точки.

Оскільки , то:

(1.7)

Нехай за проміжок часу швидкість точки змінилась віддо:

Я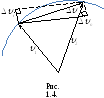к видно з рис. 1.4:

(1.8)

,(1.9)

де - тангенціальне прискорення, яке визначає зміну вектора швидкості по модулю та напрямлене по дотичній до траєкторії руху ,

- нормальне прискорення, яке визначає зміну вектора швидкості по напрямку, напрямлене до центру кривизни траєкторії. Відповідно повне прискорення:

(1.10)

Кінематика обертального руху

Обертальний рух тіл можна характеризувати поворотом на деякий кут Δφ. Для випадку, якщоΔφє достатньо малим для того, щоб вказувати напрям повороту, величинуΔφ зображають вектором, модуль якого рівний, а напрям якого визначається за правилом правого гвинта. Якщо ручку гвинта повертати в напрямку руху тіла, то рух гвинта покаже напрям вектора. Введені таким чином вектори можна складати за правилом паралелограма, а називають їх псевдовекторами.

Фізична величина, яка визначається із співвідношення:

(1.11)

називається кутовою швидкістюобертального руху тіла. Напрям кутової швидкості визначається за правилом правого гвинта і напрямлена вздовж осі обертання. Якщо, то маємо випадок рівномірного обертання. Для такого обертання. Воно характеризуєтьсяперіодом – тривалістю одного повного обертання:

(1.12)

Рівномірний рух по колу характеризується частотоюобертання – кількістю обертань за одиницю часу:

(1.13)

Кутова швидкість може змінюватись за рахунок зміни лінійної швидкості обертання тіла навколо осі і внаслідок повороту осі обертання в просторі. Фізична величина, яка визначається із співвідношення:

(1.14)

називається кутовим прискореннямтіла.

Знайдемо зв’язок між лінійною і кутовою швидкостями тіла. Нехай за часΔtтіло, що обертається навколо осі здійснило поворот на кутΔφ. При цьому його переміщення нехай буде рівнимΔS(рис. 1.5).

Як ми знаємо, модуль швидкості тіла:

(1.15)

Отже:

Знайдемо вираз, який пов’язує вектори і. Нехай матеріальна точка обертається навколо деякої осі і її кутова швидкість напрямлена вздовж цієї осі. Як видно з малюнка, вектор швидкостіперпендикулярний до площини, утвореної векторамиі. Знайдемо модуль вектора швидкості:

(- радіус кола)

(1.16)

(1.17)

Модуль вектора швидкості дорівнює модулю векторного добутку і, а напрямок визначається за правилом правого свердлика¹:

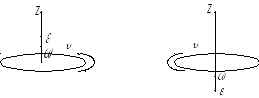
Рис. 1.6

Так як нормальне прискорення при обертальному русі напрямлене до центра кола вздовж радіуса, то воно визначатиметься із співвідношення:

, (1.18)

де - одиничний вектор, який напрямлений по радіусу кола.

(1.19)

(1.20)

У векторній формі, відповідно: (1.21)

Слід відмітити, що зв’язок між лінійним і кутовим прискоренням можна знайти, скориставшись правилом диференціювання векторного добутку:

(1.22)

Розглянемо приклади руху:

а) рівномірний прямолінійний рух.

,(1.23)

б) рівномірний рух по колу.

,(1.24)

в) рівнозмінний прямолінійний рух.

,,(1.25)

г) рівнозмінний рух по колу.

,,(1.26)