4.3.4. Необходимое условие интегрируемости функции

Теорема 4.5. Если функция интегрируема на отрезке [ ; ], то она ограни-

ограничена, но не интегрируема на любом отрезке [ ; ].

Решение. По определению | ( )| 6 1 при любых , т.е. функция Дирихле ограничена на любом отрезке [ ; ]. Покажем, что она не является интегрируемой.

Произведем разбиение отрезка [ ; ]:

лению определенного интеграла, т.е. функция Дирихле не интегрируема на любом отрезке [ ; ].

4.3.5. Достаточные условия интегрируемости

Теорема 4.6. Если функция непрерывна на отрезке [ ; ], то она интегрируема на [ ; ].

Доказательство этой теоремы приводить не будем, так как оно достаточно сложно.

Заметим лишь, что условие непрерывности функции является достаточным условием, но не необходимым.

Можно показать, в частности, справедливость следующих утвержде-

ний.

Теорема 4.7. Если функция ограничена на отрезке [ ; ] и имеет конечное число точек разрыва первого рода, то она интегрируема на отрезке [ ; ].

Теорема 4.8. Если функция ограничена и монотонна на отрезке [ ; ], то она интегрируема на отрезке [ ; ].

Например, функция ( ) = cos2 + является интегрируемой на любом отрезке [ ; ], так как она непрерывна на R.

Функция ( ) = sign (??) является интегрируемой на отрезке [−1; 1], так как только в точке = 0 она имеет точку разрыва 1-го рода.

Функция ( ) = 1/ при (0; 1] и (0) = 0 не является интегрируемой на отрезке, потому что она не ограничена на [0; 1].

4.3.6.Интеграл с переменным верхним пределом. Существование первообразной для непрерывной функции.

Важную роль в интегральном исчислении имеет связь между определенным и неопределенным интегралами. Перейдем к ее исследованию.

Пусть функция является интегрируемой на отрезке [ ; ]. Фиксируем произвольное [ ; ].

Функция будет интегрируемой на отрезке [ ; ], т.е. существует ин-

теграл

∫

( ) .

Теперь каждому [ ; ] поставим в соответствие число, равное ∫ ( ) . Это означает, что на отрезке [ ; ] будет определена фунция

∫

Φ( ) = ( ) . (4.25)

Определение. Функция Φ( ), определенная формулой (4.25), называется

интегралом с переменным верхним пределом.

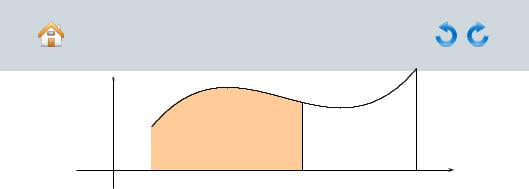
Геометрический смысл интеграла с переменным верхним пределом состоит в том, что он численно равен площади криволинейной трапеции, расположенной над отрезком [ ; ] (рисунок 4.5).

Теорема 4.9. Если функция непрерывна на отрезке [ ; ], то функция Φ,

определяемая формулой (4.25), является дифференцируемой на [ ; ], при-

[Доказательство]

Иначе говоря, теорема 4.9 утверждает, что производная от интеграла с переменным верхним пределом равна значению подынтегральной функции в точке, равной верхнему пределу.

Теорему 4.9 можно переформулировать следующим образом:

∫

ее первообразной на [ ; ]. Следовательно,

∫

( ) = Φ( ) + .

4.3.7. Формула Ньютона—Лейбница.

Названная формула считается основной формулой интегрального исчисления. Она позволяет свести вычисление определенного интеграла от непрерывной функции к вычислению разности значений любой ее первообразной на верхнем и нижнем пределах интегрирования.

Теорема 4.10. Если функция ( ) непрерывна на отрезке [ ; ] и ( )— какая-либо ее первообразная, то справедлива формула Ньютона—Лейбни- ца

∫

[Доказательство]

Разность ( ) − ( ) принято обозначать ( ) . Поэтому формулу

Поэтому, применяя формулу Ньютона—Лейбница, имеем: