2.4 Цифрлық компаратор

Екі n-разрядты екілік А және В сандарын салыстыру үшін арналған. Осы есепті шешу үшін алдымен А және В сандарының әр разрядын салыстырады. Осы операцияны орындайтын логикалық элемент екі модуль бойынша сумматор. Оған мына теңдеу сәйкес келеді:

бұл теңдеу А=В болғанда ғана Y шығыс сигналы төменгі деңгейде болады. Бұл операцияны көп кірісті элемент ЖӘНЕ төменгі деңгейдегі кіріс сигналдары үшін орындайды. Осы элементтің шығыс сигналы Q мынаған тең:

Осылайша n разрядты цифрлық компаратор (6 сурет) екі модулі бойынша қосу операциясын орындайтын n элементтен және инверсті сигна­л бойынша ЖӘНЕ элементінің бір n- кірісінен тұрады.

3. ТАҚЫРЫП. Сумматор

Жоспар

1. Жартылай сумматор. Бір разрядты сумматор

3.2 Сумматор тізбекті тасымалдаумен. Сумматор параллелді тасымалдаумен

Сумматор – көпразрядты сандарды қосу операциясын орындайтын логикалық құрылғы.

3.1 Жартылай сумматор

Бір разрядты екілік а және в сандардың қосындысы келесі кестеге сәйкес жасалады:

a	b	S	C
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Одан S қосындысы және С тасылмалдауы мына формуламен есептелінеді:

S=,C=, С=

НЕМЕСЕ-ЕМЕС элементіне келтіру үшін бұл формуланы өзгертейік:

S=

C= a∙b=

Алынған формулалар негізінде жартылай сумматор синтезделуі мүмкін. Жартылай сумматор бұл бір разрядты екі сандардың қосындысын орындайтын құрылғы. (сурет 7а)

Жартылай сумматор үшін дизъюнктивті форманы құру барысында:

S=C=a∙b

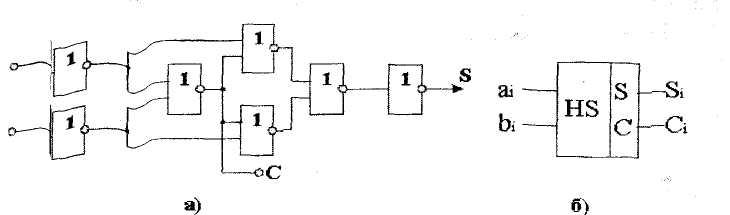
Сурет 7 Жартылай сумматордың схемасы мен оның белгіленуі.

Бірразрядты сумматор

Жартылай сумматормен салыстырғанда оған тағы төменгі разрядтан тасымалдау сигналы қосылады. Егер ол болмаса, онда жоғары разрядқа тасымалдау тек екі сан бірге (1) тең болса ғана жасалуы мүмкін.

Егер төменгі разрядтан тасымалдау болса, онда жоғарғы разрядқа тасымалдау әр қашан болады, тек екі сан нөлге тең болса ғана тасымалдау болмайды.

Осындай сумматор схемасы 2 жартылай сумматормен жасалады. (8 сурет)

Бұл схемада аралық сигналдарын қарастырайық. Бұл сигналдарды ақиқат кестесіне қосайық. Бұл схема жұмысының және кестесінің сәйкестігін барлық мүмкін болатын нұсқаларын қарап тексеруге болады.

Сурет 8. Толық сумматордың схемасы

Сумматордың ақиқат кестесі

Кірістері			Аралық мәндер			Шығыстары
ai	bi	ci	pi	gi	ri	si	ci+1
0	0	0	0	0	0	0	0
0	0	1	0	0	0	1	0
0	1	0	1	0	0	1	0
0	1	1	1	0	1	0	1
1	0	0	1	0	0	1	0
1	0	1	1	0	1	0	1
1	1	0	0	1	0	0	1
1	1	1	0	1	0	1	1

3.2 Тізбекті тасымалдауы бар сумматор

Ол бірразрядты толық сумматорлар негізінде құралады. Толық сумматордың әр біреуі төменгісінен басқасы, үш кіріс сигналын (2 қосылатын және төменгі разрядтан тасымалдау сигналы) қабылдау қажет.

9 суретте екі төрт разрядты а және в сандарын қосуға арналған схема көрсетілген. С₄ тасымалдау сигналы ақиқат болады егер С₃ мәні дұрыс болса. Осындай сумматорлар Тізбекті тасымалдауы бар сумматор деп аталады.

Төмендегі схема интегралды түрде шығарылады. Оның төменгі разрядында толық сумматор қолданылады, схеманың разрядтілігін жоғарлату үшін.

Сурет 9. Тізбекті тасымалдауы бар сумматордың схемасы

Параллельді тасымалдауы бар сумматор. Көп разрядты сандарды қосу уақытын азайту үшін параллельді тасымалдаумен сумматорлар қолданады (сурет 10). Барлық тасымалдау сигналдары кіріс айнымалылардың мәндері бойынша есептелінеді.

Сурет 10. Параллельді тасымалдауы бар сумматордың схемасы

Кез келген і-ші разрядты тасымалдау сигналы үшін мына теңдеуді қолдануға болады:

c_i+1=a_i ∙ b_i + (a_i b_i) ∙ c_i = g_i + p_i ∙ c_i (*)

Толық сумматорда да g_i, р_i мәндері аралық нәтиже ретінде есептелінеді. g_i сигналы тек осы разрядтағы a_i және b_i кіріс айнымалылардың комбинациясынан тасымалдау жасалса ғана шығарылады. Сондықтан оны тасымалдауды генерациялау функциясы деп атайды. р_i сигналы төменгі разрядта алынған c_i тасымалдау сигналы ары қарай жіберіле ме, жоқ па соны көрсетеді. Сондықтан оны тасымалдауды тарату функциясы деп атайды.

(*) теңдеуден тасымалдау сигналын есептейтін келесі формулаларды шығаруға болады:

C₁=g₀ + p₀ ∙ c₀,

C₂= g₁ + p₁ ∙ c₁= g₁ + p₁ ∙ g₀ + p_{1 ∙} p₀ ∙ c₀,

C₃= g₂ + p₂ ∙ c₂ = g₂ + p₂ ∙ g₁ + p₂ ∙ p₁ ∙ g₀ + p₂ ∙ p_{1 ∙} p₀ ∙ c₀

C₄= g₃ + p₃ ∙ c₃ = g₃ + p₃ ∙ g₂ + p₃ ∙ p₂ ∙ g₁ + p₃ ∙ p₂ ∙ p₁ ∙ g₀ + p₃ ∙ p₂ ∙ p_{1 ∙} p₀ ∙ c₀