7.1. Пластинаның көлденен ағысы кезіндегі жылуберудің есептік формулалары.

температурасы бар және ламинарлы тәртіп кезіндегі жазық беттің бойымен ағынның қозғалысы кезіндегі

сұйық тамшысы үшін:

; (111)

ауа үшін:

. (112)

Турбулентті тәртіп кезінде :

сұйық тамшысы үшін:

; (113)

ауа үшін:

. (114)

Анықталатын болып жүгіруші ағын температурасын аламыз( саны температурасы бойынша анықталады), анықталатын геометриялық өлшем ретінде – ағын бойынша бағытталған қабырғанын ұзындығын l аламыз. Есеп-қисапты қосымшадағы П. 7-суреттегі ,номограмма бойынша жүргізуге болады.

Пластинаның алдынғы жиегінен х ара қашықтығы кезіндегі жылуберудің жергілікті коэффициентін келесі формулалар бойынша анықтауға болады:

Шекаралық қабаттағы ағыстың ламинарлы тәртібі кезінде:

; (115)

турбулентті тәртіп кезінде:

. (116)

Пластинаның алдынғы жиегінен х ара қашықтығы кезіндегі шекаралық қабаттың жылулық κ және гидродинамикалық δ қалыңдықтарын келесі формулалар бойынша наықтауға болады:

ламинарлы тәртіп кезінде:

(117)

турбулентті тәртіп кезінде:

. (118)

Ламинарлы тәртіп кезінде, ұзындығы , алдынғы бастапқы бөлігі қыздырылмайтын пластина үшін (9-сурет) келесі формула дұрыс болады:

, (119)

мұндағы және l — пластинаның қыздырылатын және толық ұзындығы. Ал геометриялық өлшемі— тең.

7.2. Құбыр(арна ) ішіндегі ағынның қозғалысы кезіндегі жылуберу.

Дөңгелек құбырдың бастапқы аймағында, гидродинамикалық және жылулық шекаралық қабаттың қалыптасуы жүреді, яғни құбырдың көлденен ағысы толғанша, шекаралық қабаттың қалыңдығы арта береді.

Бұл құбырдың бастапқы аймақтары деп, шекаралық қабаттың дамуына қарай жылуберудің құлауын сипаттайтын, сәйкесінше гидродинамикалық( ұзындығы) және жылулық (l_т ұзындығы) бастапқы аймақтарын айтамыз.

Бастапқы аймақтан кейін сұйықтың ағысы мен жылуалмасу тұрақтанады, яғни барлық көлденен ағыста жылдамдықтар өрісі мен жылуберу бірдей болады. Олай болса, және кезіндегі ұзын құбырлар үшін, толғымен тұрақталған ағындағы жылуберуді сипаттайтын, орташа жылу беру санымен анықталады. Ал қысқа құбырлар үшін бірдей шарттағы ұзын құбырлармен салыстырғанда жылуберу жоғары болады.

Арнаның көлденен ағыс формасы	Эквиватентті диаметр	коэффициенті	коэффициенті
Дөңгелек ағыс, -ішкі диаметр		0,065	0,055	0,07
Сақиналы ағыс, ішкі диаметрдің сыртқы диаметрге қатынасы,		0,010—0,015	0,05	0,06
а және b жақтары бар тікбұрышты ағыс ,		0,023—0,075	—	—

Гидродинамикалық және жылулық тұрақталған бастапқы аймақтардың ұзындығы келесі формуламен анықталады:

және , (120)

Мұндағы және —арна формасынан тәуелді коэффициенттер (кестеге қара); — арнаның көлденен ағысының П периметрі және f ауданы бойынша анықталған арнанын эквивалентті диаметрі және ол келесі формула бойынша анықталады:

. (121)

қолдану , өте үлкен бұрыштары жоқ арналарда ортаның турбулентті қозғалысы кезінде қанағаттанарлық мән беретінін көруге болады.

А. Дөңгелек жазық құбырда (Rе_ж<2000) , еркін конвекцияның жоқтығы кезінде ламинарлы тәртіп - тұтқырлы деп, ал еркін конвекцияның жоқтығы кезінде ламинарлы тәртіп – гравитациялы- тұтқырлы деп аталады. Бір тәртіптен екінші тәртіпке ауысу, шекаралық қабаттың анықталатын температурасы кезінде болатын, санымен анықтауға болады.

кезіндегі қозғалыстың тұтқырлы тәртібі үшін, кезіндегі, құбырдың орташа ұзындығы бойынша Нуссельт саны келесі түрде анықталады:

, (122)

мұндағы l және — құбырдың ұзындығы мен ішкі диаметрі.

(122) формула кезінде және динамикалық тұтқырлық коэффициентерінің қатынасы кезінде жағдай үшін әділ болады. көбейткіші тамшылы сұйықтар үшін ғана қолданылады. Анықталатын өлшем – құбырдың ішкі диаметрі. Gr, Рr, , Ре, үшін анықталатын температура қабылданады, егер құбыр ұзындығы бойынша сұйықтықтың температурасы аз өзгерсе Gr саны үшін келесі температура қабылданады. Ал қарама-қарсы жағдай кезінде, , , үшін температурасы қабылданады, мұндағы қабырғаның орташа температурасы кезіндегі , орташа логарифмдік қысым , (95)-формуламен анықталады.

Осының өзінде сұйықтықтың физикалық қасиеттері Gr және Рr үшін , ал алынады. Гидродинамикалық бастапқы аймаққа енгізілген келесі формула бойынша анықталады:

,

бұл кезінде әділ келеді. Егер , онда .

кезіндегі тұтқырлы- гравитациялық тәртіп үшін, ұзындығы l горизонтальді құбыр үшін келесі формула сәйкес келеді:

. (123)

(123) формула, ; ; ; кезінде әділ.

Вертикалды құбырларда мәжбүрлі және еркін конвекция бағыттарының сәйкес келуі кезінде қабырғадағы орташа жылу беру келесі формула бойынша анықталады:

; (124)

Мұндағы ;.

формула кезінде әділ болады;

; .

Вертикалды құбырларда мәжбүрлі және еркін конвекция бағыттарының қарама-қарсы келуі кезінде қабырғадағы орташа жылуберу келесі формула бойынша анықталады:

, (125)

Мұндағы n=0,11 сұйықтықтың қыздыруы, n=0,25 суытуы кезінде.

Бұл формула және кезінде әділ.

Тұрақтанған жылуалмасу аймағындағы сұйық металл үшін жылу алмасу келесі қатынаспен анықталады:

егер . (126)

Б.Ә р түрлі көлденен ағысы бар арналар мен тік құбырлардағы сұйықтықтың турбулентті ағысы үшін М. А. Михеева формуласы сәйкес келер еді:

. (127)

Тұрақты физикалық қасиеттері бар екі атомды газдар үшін келесі формуланы қолдануға болады:

. (128)

жылуберу коэффициенті , мұндағы (95) формула бойынша анықталады. Геометриялық өлшемді анықтайтын дөңгелек құбырлар үшін – ішкі диаметр, дөңгелек емес арналар үшін – эквивалентті диаметр алынады, және олар (121) формулалар бойынша анықталады. (127) формула және кезінде әділ болады. Коэффициент бастапқы жылулық бөлікке әсері кезінде ескереді: егер ; егер қосымшадағы 9-кесте бойынша анықталады. (127) формула бойынша номограмма бойынша есептеу қосымшадағы П.7 суретте келтірілген.

Сұйықтықтың ауыспалы физикалық қасиеттері кезіндегі тұрақтанған жылуберу үшін келесі формула ұсынылады (Б. С. Петухов пен қызметкерлері ұсынған)

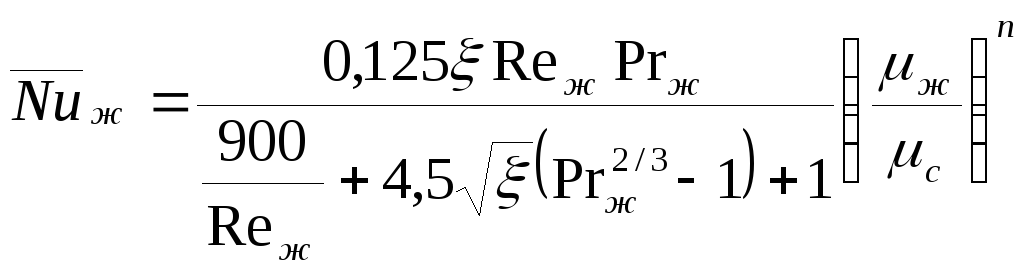, (129) мұндағы n=0,11 сұйықтықтың қыздыруы , n=0,25 суытылы кезінде; — жазық тегіс құбыр үшін арналған гидравликалық кедергі коэффициенті. Бұл формула ; ; кезінде әділ. Анықталатын өлшем- құбырдың ішкі диаметрі.

Динамикалық тұтқырлықтың қатынастары тек тамшылы сұйықтар үшін ғана қоладнылады.

Құбырлар мен арналарда турбулентті ағыс кезіндегі газдың физикалық қасиеттерінің өзгеруі кезіндегі жылуберуді ескеріп:

қыздыру кезінде

, (130)

егер ;

салқындату кезінде:

, (131) егер.

Температуралық фактор:

. (132)

Анықталатын өлшем— құбырдың ішкі диаметрі (эквивалентті диаметр ).

Дөңгелек құбырда таза сұйық металдың ағысы және кезінде

орташа жылу беру келесі формуламен анықталады:

; (133)

кезінде ; кезінде .

(133) формула , кезінде қолданылады.

Сыртқы диаметрі және ішкі диаметрі үшін , сақиналы арналарда, ішкі қабырғадағы (сырты оқшауланған )турбулентті тұрақталған жылуберу ағысы келесі формула бойынша анықталады:

, (134) мұндағы ; ; , — қабырғаның ішкі бетіндегі температура.

Қабырғаның сыртқы бетіндегі(ішкі беті оқшауланған) жылуберу келесі формуламен анықталады:

, (135) мұндағы ; ; — қабырғаның сыртқы бетіндегі температура.

(134) және (135) формулаларындағы — Нуссельт саны, эквивалентті диаметрі бар , (127) формула бойынша анықталған. Түзету коэффициенті , егер , және , егер . (134) және (135) формулалар үшін , және тура келеді.

Сақиналы құбырда қабырғаның ішкі жылуберуі кезіндегі жылулық тұрақталған аймақтың ұзындығын анықтау үшін келесі формула қолданылады:

, (136) ал сыртқы қабырғадағы жылуберу кезінде:

. (137)

Егер сақиналы арнаның ұзындығы аз және тең болса, және қабырғаның ішкі бетіндегі жылуалмасу кезінде болса, қабырғаның сырқы бетіндегі жылуалмасу болса , (134) және (135) бойынша анықталған және жылуберу коэффициенттерін коэффициентіне көбейту керек.

B. Құбырдың ішкі диаметрі және орташа иілу диаметрі D бар, иілген құбырлардағы ағынның қозғалысы кезіндегі жылуберу интенсивті центрден тепкіш эффектінің пайда болуынан туындайды.

Жылуберуді анықтау кезінде екі Рейнольдс: и ( кезінде) санымен салыстырылатын санымен анықталады.

Егер кезінде , онда жылуберу мен кедергіні есептеу тік құбырлардағы ламинарлы тәртіп үшін арналған формулалармен анықталады. Егер болса , онда арналардағы турбулентті ағыс үшін арналған (127) формуламен анықталады. Егер болса , онда жылуберу коэффициенті (127) формула бойынша анықталар еді және көбейтілер еді.

Г. Газ бен сұйықтықпен суытылатын құбырларда бойлық түрде ағатын бір буда үшін келесі формула келеді:

. (138)

мұндағы ; ; құбырлардың үшбұрыш бойынша орналасуы кезінде , құбырлардың төртбұрыш бойынша орналасуы бойынша ; s — құбыр осьтерінің арасындағы ара қашықтық(қадам); — құбырдың сыртқы диаметрі; — геометриялық өлшемін анықтаушы.

Бұл формула ; ; ; кезінде әділ.

Көлденен қалқалары жоқ, бүркеніш құбырлы жылуалмастырғыштардың құбыр аралық кеңістігіндегі анықтаушы өлшемі бар

, (139)

Nu саны (127) формула бойынша анықталады.

мұндағы — бүркеніштің ішкі диаметрі; — құбырдың сыртқы диаметрі, м; n — құбырдағы буда саны; V — көлемдік шығын, ; - құбыр аралас кеңістіктегі ағынның орташа жылдамдығы.

Егер s қадамы белгілі болса, онда құбырлары шаршы (төртбұрышты) сияқты орналасқан будалар үшін

, (140)

ал шахмат тәріздес(үшбұрышты) орналасқан будалар үшін:

. (141)

Құбыр араларындағы кеңістіктегі көлденен қалқалары бар жылуалмастырғыштар үшін:

будада құбырлардың сенек тәріздес орналасуы кезінде:

, (142)

будада құбырлардың шахмат тәріздес орналасуы кезінде:

. (143)

Анықталатын өлшем —құбырдың сыртқы диаметрі, жылдамдық орташа минималды ағыс бойынша анқталады:

егер қалқалар сегмент типті болса,

; (144)

егер қалқалар құрама типте болса,

. (145)

Мұнда h — іргелес қалқалар арасындағы ара қашықтық; қадам көбінесе келесі түрде анықталады: .