
2.4 Метод Зейделя
Будем
снова рассматривать исходную систему
(2.1) и эквивалентную ей приведенную
(2.4). Основная идея метода Зейделя состоит
в том, что на каждом шаге итерационного
процесса при вычислении очередного
приближения к решению
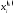 используются уже к этому моменту
полученные
используются уже к этому моменту
полученные . Начальные приближения к решению системы
(2.1) подставим в первое уравнение
системы(2.4) и вычислим новое значение
. Начальные приближения к решению системы
(2.1) подставим в первое уравнение
системы(2.4) и вычислим новое значение .
Используя только что вычисленное
.
Используя только что вычисленное и начальные значения
и начальные значения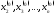 ,
вычислим из второго уравнения системы
(2.4) новое значение
,
вычислим из второго уравнения системы
(2.4) новое значение ,
и т.д. Используя
,
и т.д. Используя найдем новое значение
найдем новое значение из последнего уравнения. В общем случае
(k+1)
приближение к решению системы (2.1) можно
записать:
из последнего уравнения. В общем случае
(k+1)
приближение к решению системы (2.1) можно
записать:
 (2.10)
(2.10)
или
 (2.11).
(2.11).
Условия сходимости и условие окончания итерационного процесса те же самые, что и для метода простой итерации.
Преимущество метода Зейделя состоит в том, что он обеспечивает более быструю сходимость, чем метод простой итерации.
Учитывая, что условия сходимости не являются необходимыми, и что «вручную» приводить исходную систему (2.1) к виду (2.4) неудобно (особенно для большего числа уравнений), на практике на практике пользуются следующим приемом.
Умножим
левую и правую части системы (2.1), в
матричной форме (2.2) слева на матрицу
 ,
получим
,
получим .
Обозначим
.
Обозначим ,
, .
Получили новую систему
.
Получили новую систему
 (2.12),
(2.12),
равносильную исходной (2.2). Преобразованную систему (2.12) называют нормальной. Существует теорема, которую приведем без доказательства.
Теорема.
Итерационный процесс Зейделя для приведенной системы эквивалентной нормальной системе (2.12) всегда сходится к единственному решению этой системы, при любом выборе начального приближения.
Блок-схема
алгоритма решения системы и линейных
уравнений методом Гаусса – Зейделя
представлена на рисунке 2.5. В качестве
исходных данных вводятся коэффициенты
и правые части уравнений системы,
погрешность
 ,
допустимое число итераций
,
допустимое число итераций
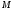 ,
а также начальные приближения переменных
,
а также начальные приближения переменных
 .
Отметим, что начальные приближения
можно не, вводить в ЭВМ, а полагать их
равными некоторым значениям (например,
нулю).
.
Отметим, что начальные приближения
можно не, вводить в ЭВМ, а полагать их
равными некоторым значениям (например,
нулю).
Для
удобства чтения блок-схемы объясним
некоторые обозначения: k
- порядковый номер итерации; i
— номер уравнения, а также переменного,
которое вычисляется в данном цикле; j
— номер члена вида
 .
Итерации прекращаются либо после
выполнения условия
.
Итерации прекращаются либо после
выполнения условия
 ,
либо при
,
либо при .
В последнем случае итерации не сходятся,
и после
.
В последнем случае итерации не сходятся,
и после итераций счет прекращается без выдачи
результатов. Можно предусмотреть в этом
случае также и вывод на печать некоторой
поясняющей информации.
итераций счет прекращается без выдачи
результатов. Можно предусмотреть в этом
случае также и вывод на печать некоторой
поясняющей информации.
