
2.2 Метод Гаусса
Пусть система алгебраических уравнений (2.1) имеет единственное решение (матрица А невырождена). Метод Гаусса– это метод последовательного исключения неизвестных. Суть его состоит в преобразовании системы (2.1) к системе с треугольной матрицей, из которой затем последовательно обратным ходом получаются значения всех неизвестных.
Предположим,
что
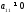 (этого условия можно добиться перестановкой
уравнений системы). Введёмn-1
сомножитель
(этого условия можно добиться перестановкой
уравнений системы). Введёмn-1
сомножитель
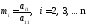 и вычтем из каждого
i-го
уравнения первое, помноженное на
и вычтем из каждого
i-го
уравнения первое, помноженное на
 .Преобразованная
система уравнений запишется в следующем
виде:
.Преобразованная
система уравнений запишется в следующем
виде:
 ,
где
,
где
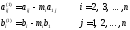 ,
во всех уравнениях, начиная со второго
,
во всех уравнениях, начиная со второго для
для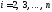 .
.
Затем,
оставим первое уравнение в покое, мы
можем исключить
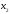 из последних
из последних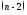 уравнений, затем
уравнений, затем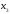 из последних
из последних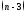 уравнений и т. д., вместо системы (2.1)
получим равносильную ей систему с
треугольной матрицей:
уравнений и т. д., вместо системы (2.1)
получим равносильную ей систему с
треугольной матрицей:
 (2.3)
(2.3)
На
некотором k-ом
элементе мы исключаем
 с помощью множителей
с помощью множителей ,
, .
Причём предполагается, что
.
Причём предполагается, что .
Тогда
.
Тогда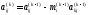 ,
, ,
для
,
для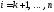
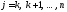
 .
.
При
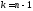 происходит исключение
происходит исключение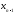 из последнего уравнения. На этом
завершается первый этап решения методом
Гаусса.
из последнего уравнения. На этом
завершается первый этап решения методом
Гаусса.
Такая система (2.3) называется треугольной. Теперь очевидно, что надо делать для решения системы: определить xn из последнего уравнения и подставить результат в n-1 уравнение и т. д. Этот процесс называется обратной подстановкой.
Отметим, что процесс исключения неизвестных не изменяет абсолютной величины определителя системы, хотя знак определителя и изменяется при каждой перестановке уравнений. После окончания процесса, значение определителя равно произведению диагональных элементов, причём знак этого произведения надо изменить на обратный, если количество перестановок было нечётным.
Одной
из модификаций метода Гаусса является
схема с выбором главного элемента. Она
состоит в том, что требование неравенства
нулю диагональных элементов заменяется
более жёстким: из всех оставшихся в
каждом столбце элементов надо выбрать
наибольший по модулю и переставить
уравнения так, чтобы этот элемент
оказался на месте элемента
 .
.
2.3 Метод простой итерации
При
большом числе неизвестных линейной
системы, схема метода Гаусса становится
очень сложной, накапливаются ошибки
округления. В этом случае удобнее
пользоваться приближенными (итерационными)
методами. Итерационные методы сводятся
к построению итерационной последовательности
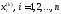 ,
сходящейся к точному решению системы
,
сходящейся к точному решению системы .
Каждый такой метод характеризуется
своей итерационной формулой. В простейшем
случае, при вычислении
.
Каждый такой метод характеризуется
своей итерационной формулой. В простейшем
случае, при вычислении используется только одна предыдущая
итерация
используется только одна предыдущая
итерация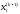 ,
гдеk-
номер итерации. Такие методы называются
одношаговыми.
,
гдеk-
номер итерации. Такие методы называются
одношаговыми.
Предполагая,
что диагональные коэффициенты
 ,
при
,
при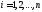 ,
разрешим первое уравнение системы (2.1)
относительно
,
разрешим первое уравнение системы (2.1)
относительно ,
второе – относительно
,
второе – относительно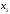 ,…,
последнее- относительно
,…,
последнее- относительно .
В результате получим систему, которая
называетсяприведенной:
.
В результате получим систему, которая
называетсяприведенной:
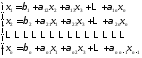 (2.4),
(2.4),
где
 ,
, .
.
Предположим,
что начальные приближения к решению
системы известны:
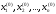 (например можно в качестве начальных
приближений принять столбец свободных
членов). Подставим эти значения в правые
части системы (2.4), получим первое
приближение
(например можно в качестве начальных
приближений принять столбец свободных
членов). Подставим эти значения в правые
части системы (2.4), получим первое
приближение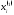 ,
затем вычисленные
,
затем вычисленные подставим снова в правую часть приведенной
системы (2.4) и т.д., т.е. строим итерационный
процесс и на некоторомk-
шаге получим:
подставим снова в правую часть приведенной
системы (2.4) и т.д., т.е. строим итерационный
процесс и на некоторомk-
шаге получим:
 (2.5).
(2.5).
Итерационный
процесс продолжаем до тех пор, пока все
 не станут достаточно близки к
не станут достаточно близки к .
Критерий близости можно задать в
следующем виде:
.
Критерий близости можно задать в
следующем виде: ,
для всех
,
для всех .
Достаточные условия сходимости следующие:
.
Достаточные условия сходимости следующие:
 ,
при
,
при
 (2.6)
(2.6)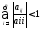 ,
при
,
при
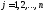 (2.7)
(2.7) ,
при
,
при
 (2.8)
(2.8)Если все
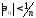 ,
при
,
при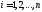 ,
, то итерационный процесс заведомо
сходится. (2.9)
то итерационный процесс заведомо
сходится. (2.9)
Справедливо следующее утверждение: если выполняется хотя бы одно из условий (2.6) –(2.9), то итерационный процесс сходится к единственному решению системы при любом выборе начального приближения.
