
- •Федеральное агентство по образованию
- •1 Цели и задачи практических занятий по дискретной математике
- •2 Содержание занятий
- •2.1 Практические занятия № 1 – 2. Множества. Операции над множествами. Свойства операций над множествами
- •2.1.1 Теоретические сведения и методические рекомендации по решению задач
- •1) , То есть;
- •2) , То есть.
- •2.1.2 Примеры решения задач
- •2.1.3 Задачи для самостоятельного решения
- •2.2.1 Теоретические сведения и методические рекомендации по решению задач
- •2.2.2 Примеры решения задач
- •2.2.3 Задачи для самостоятельного решения
- •2.3 Практическое занятие № 8. Соответствия и их свойства
- •2.3.1 Теоретические сведения и методические рекомендации по решению задач
- •2.3.2 Примеры решения задач
- •2.3.3 Задачи для самостоятельного решения
- •G1 g2
- •2.4 Практическое занятие № 9. Операции и их свойства
- •2.4.1 Теоретические сведения и методические рекомендации по решению задач
- •2.4.2 Примеры решения задач
- •2.4.3 Задачи для самостоятельного решения
- •2.5 Практическое занятие № 10. Гомоморфизмы
- •2.5.1 Теоретические сведения и методические рекомендации по решению задач
- •2.5.2 Примеры решения задач
- •2.5.3 Задачи для самостоятельного решения
- •2.6 Практическое занятие № 1112. Алгебры с одной бинарной операцией. Полугруппы. Моноиды. Группы. Подгруппы. Циклические группы. Группа подстановок
- •2.6.1 Теоретические сведения и методические рекомендации по решению задач
- •2.6.2 Примеры решения задач
- •2.7 Практические занятия № 13 – 15. Алгебры с двумя бинарными операциями. Кольца. Поля. Решетки. Булевы алгебры
- •2.7.1 Теоретические сведения и методические рекомендации по решению задач
- •2.7.2 Примеры решения задач
- •2.7.3 Задачи для самостоятельного решения
- •2.8 Практические занятия № 16 – 19. Комбинаторика
- •2.8.1 Теоретические сведения и методические рекомендации по решению задач
- •2.8.2 Примеры решения задач
- •2.8.3 Задачи для самостоятельного решения
- •2.9 Практическое занятие № 20. Контрольная работа
- •2.10 Практические занятия № 21 – 22. Орграфы и бинарные отношения. Связность. Компоненты связности
- •2.10.1 Теоретические сведения и методические рекомендации по решению задач
- •2.10.2Примеры решения задач
- •2.10.3 Задачи для самостоятельного решения
- •2.11 Практические занятия № 23 – 25. Поиск путей в графах орграфах. Минимальные пути в нагруженных орграфах. Эйлеровы цепи и циклы. Сети и потоки
- •2.11.1 Теоретические сведения и методические рекомендации по решению задач
- •2.11.2 Примеры решения задач
- •2.11.3 Задачи для самостоятельного решения
- •3 Технические и инструментальные средства
- •4 Порядок проведения занятий
- •Содержание
2.3.3 Задачи для самостоятельного решения
Пусть X={-1,-2,-3,1,2,3,0} и Y- множество всех натуральных чисел. Каждому числу xXставится в соответствие его квадрат. Выпишите все пары, принадлежащие этому соответствию. Каковы свойства этого соответствия?
С
 оответствияG1–G8определены графически на рисунке 7.
Найти образы и прообразы: чисел 1, 2, 3,
4; отрезков [2, 3], [1, 2], [2, 4], [3, 4], [3, 5]. Каковы
свойства соответствий? Для ответа на
последний вопрос определите множества
А и В:
оответствияG1–G8определены графически на рисунке 7.
Найти образы и прообразы: чисел 1, 2, 3,
4; отрезков [2, 3], [1, 2], [2, 4], [3, 4], [3, 5]. Каковы
свойства соответствий? Для ответа на
последний вопрос определите множества
А и В: .
.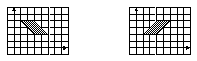
у у
G1 g2
1 1
0 1 x 0 1 x


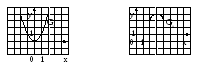
Рисунок 7 – СоответствияG1–G8
Пусть G– множество точек прямой линии, координаты которых удовлетворяют соотношению
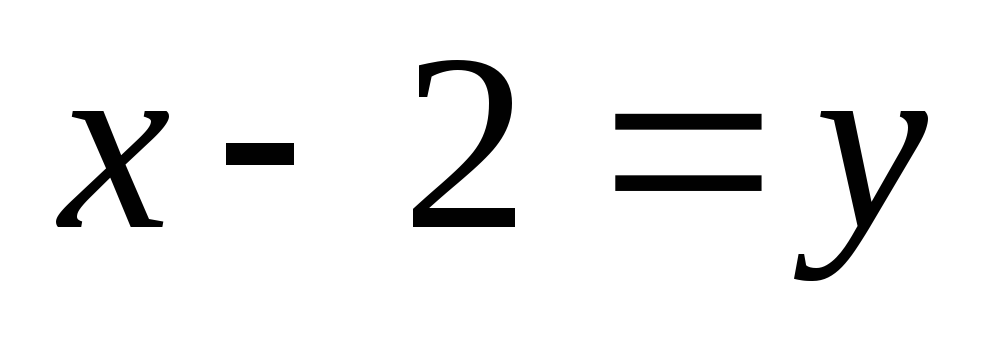 ,
,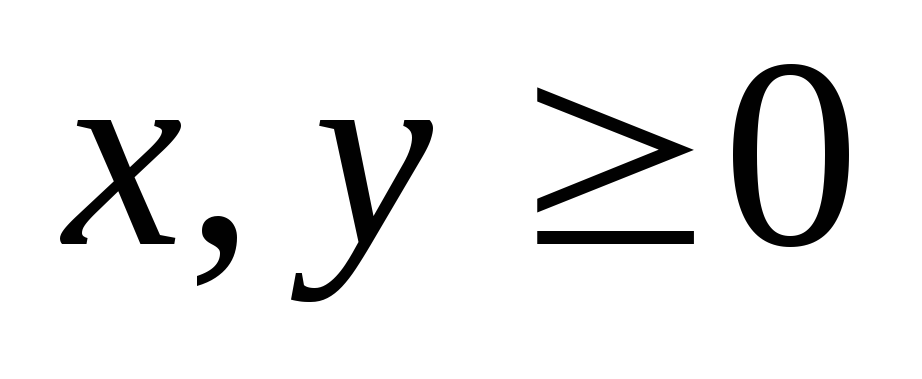 .
Каковы свойства соответствия? Является
ли соответствие взаимно однозначным?
.
Каковы свойства соответствия? Является
ли соответствие взаимно однозначным?Задать несколько типов для функций f(x):
а)
![]() ; г)
; г)![]() ;
;
б)
![]() ; д)
; д)![]() ;
;
в)
![]() ; е)
; е)![]() .
.
Для каждого из заданных типов функций
![]() определить:
определить:
а) свойства f;
б) является ли fотображением, и если – да, то каким?
в) имеет ли fобратную функциюf-1, и если имеет, то является лиf-1отображением?
Англо-русский словарь устанавливает соответствие между множествами английских и русских слов. Каковы свойства этого соответствия?
Таблица выигрышей лотереи устанавливает соответствие Gмежду парами чисел изN2(серия и номер выигравшего билета) и множеством выигрышейМ. Является ли заданное соответствие функцией? Если да, то является ли оно отображением?
Является ли функция
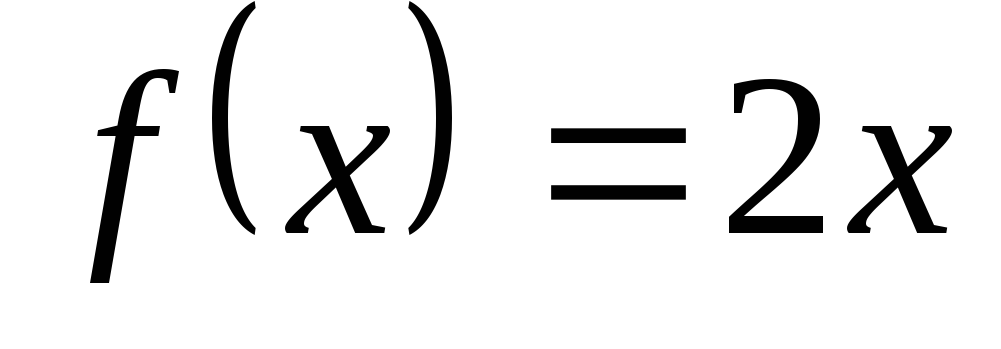 ,
имеющая тип
,
имеющая тип ,
отображением, если да, то каким? Имеет
ли эта функция обратную
,
отображением, если да, то каким? Имеет
ли эта функция обратную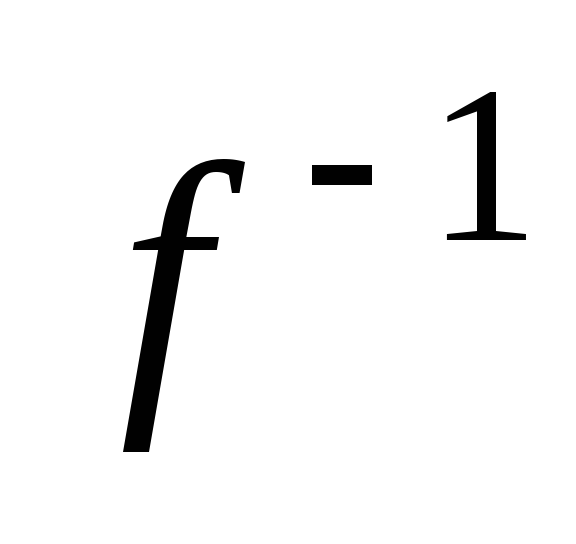 ;
если да, то является ли
;
если да, то является ли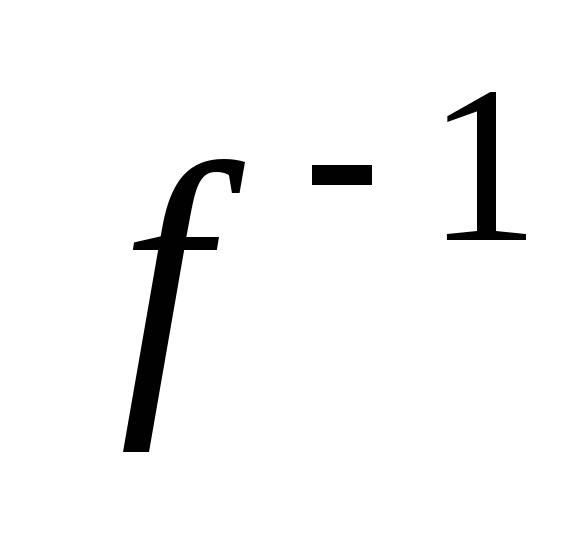 отображением?
отображением?Пусть множества
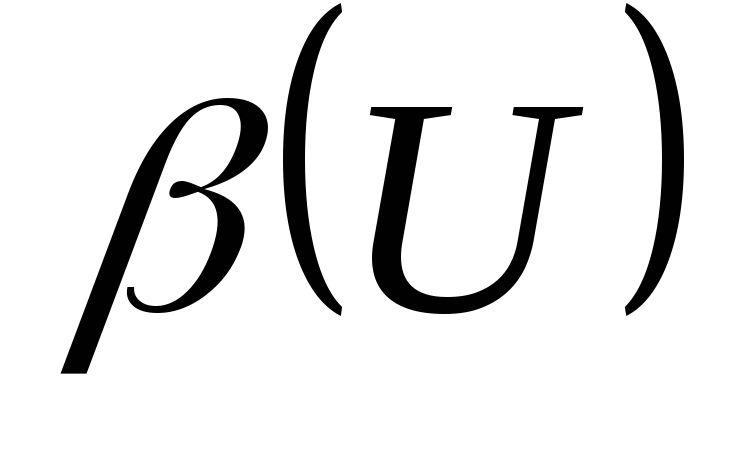 ,
где
,
где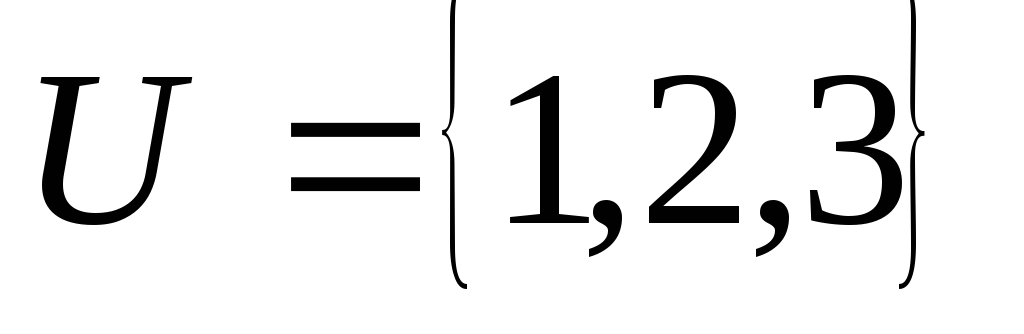 ,
и
,
и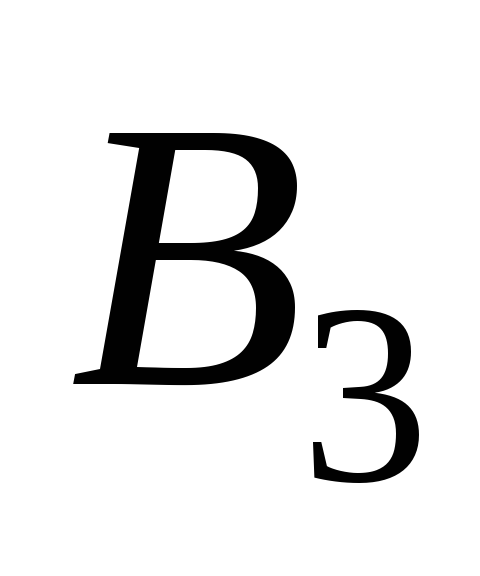 определены так:
определены так: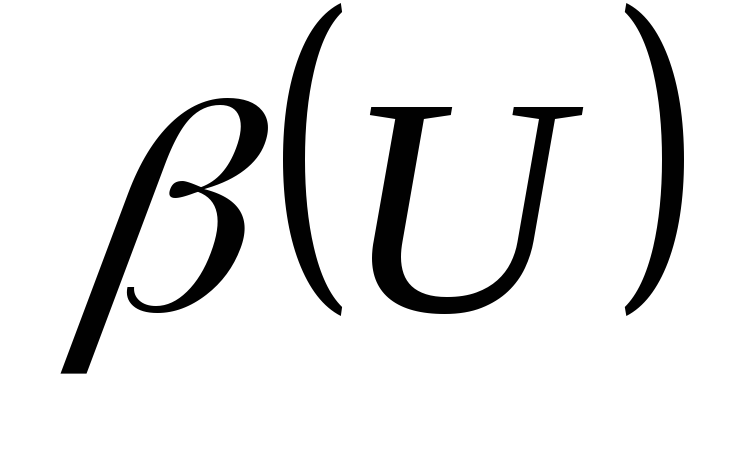 - булеан множества
- булеан множества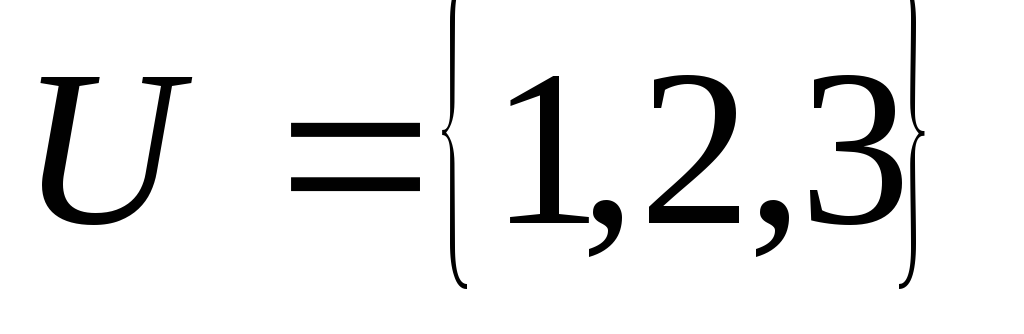 и
и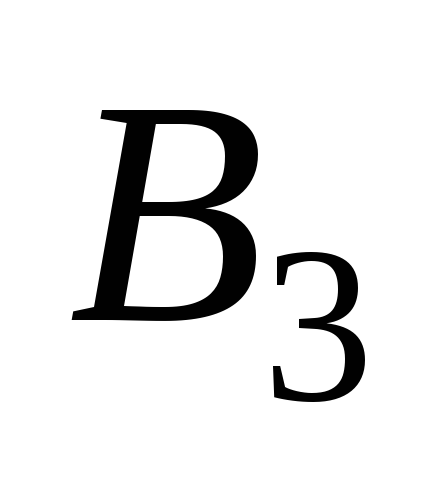 - множество всех двоичных векторов
длины 3, т.е.
- множество всех двоичных векторов
длины 3, т.е.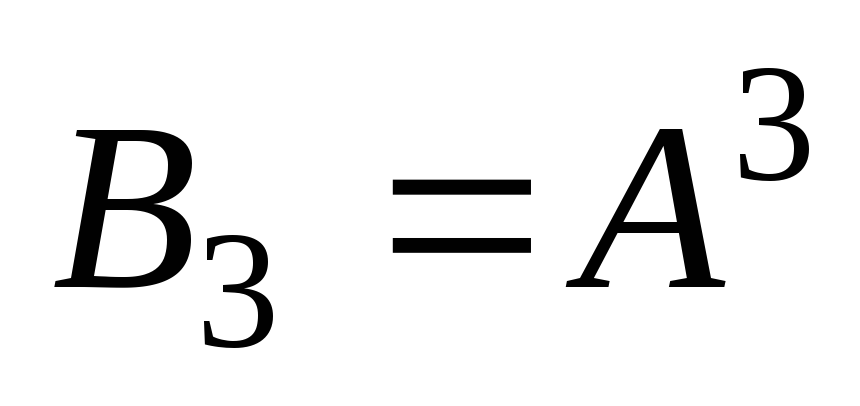 ,
где
,
где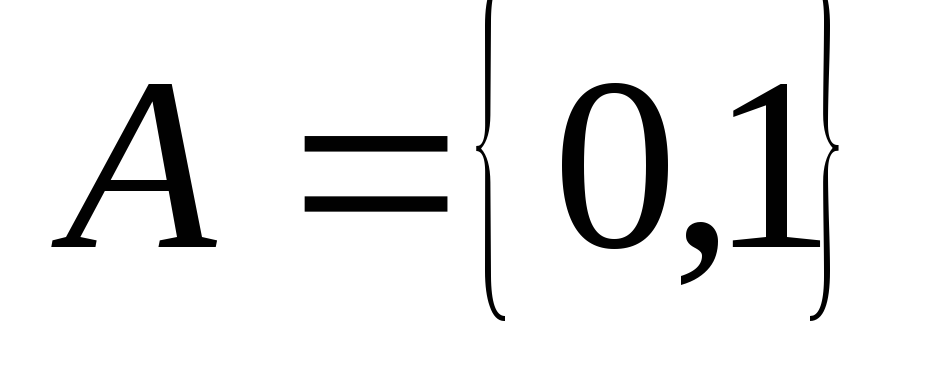 .
Показать, что между множествами
.
Показать, что между множествами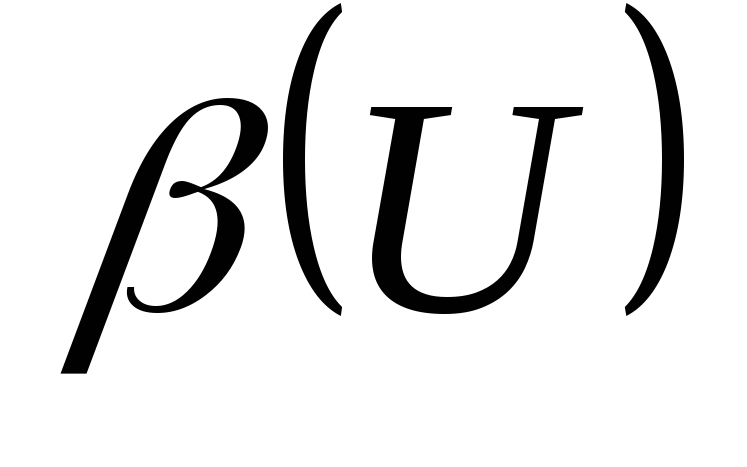 и
и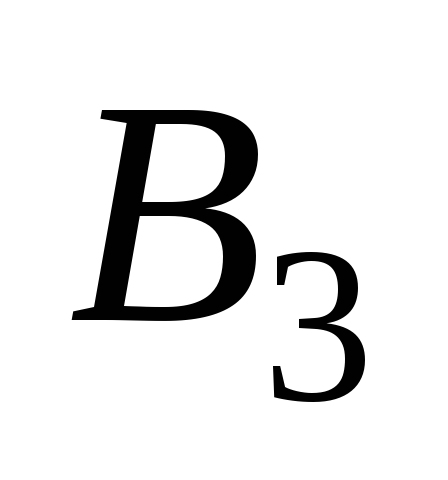 существует взаимно однозначное
соответствие.
существует взаимно однозначное
соответствие.Найти композицию функций: а)
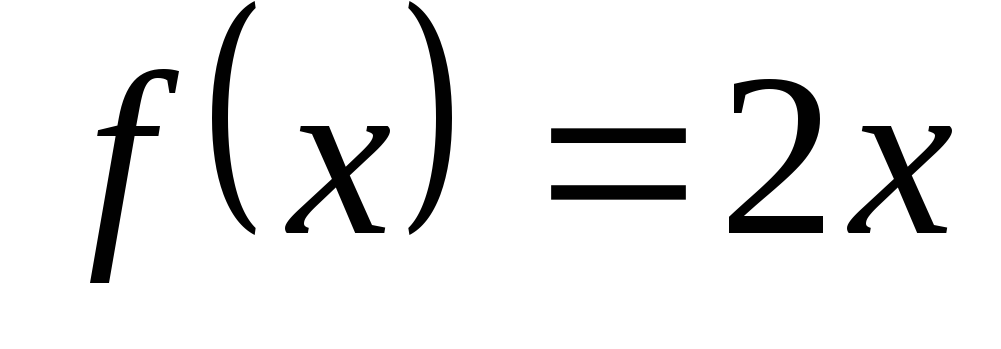 и
и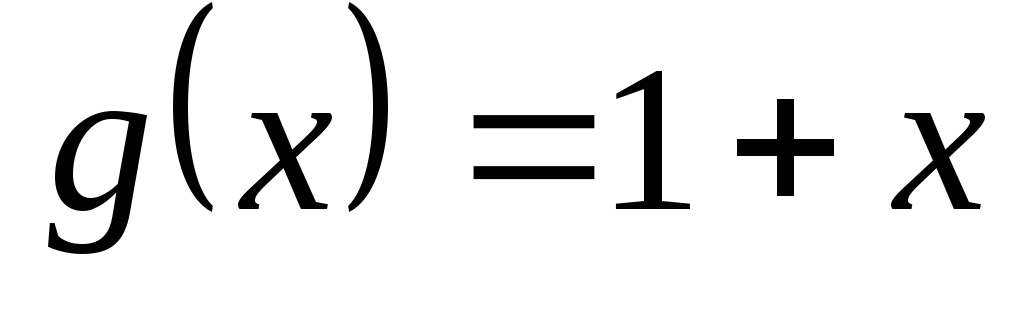 ;
;
б)
![]() и
и![]() .
Найти области определения функций и их
композиций.
.
Найти области определения функций и их
композиций.
Каковы свойства соответствия между множеством натуральных чисел Nи множеством
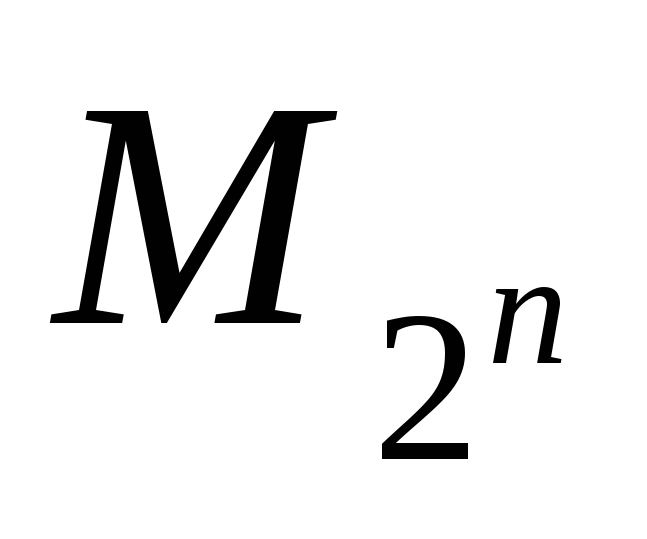 степеней двойки:
степеней двойки: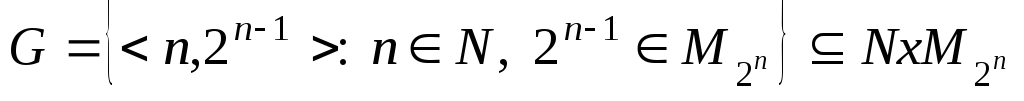 ?
Используя определение равномощности
множеств, показать, что
?
Используя определение равномощности
множеств, показать, что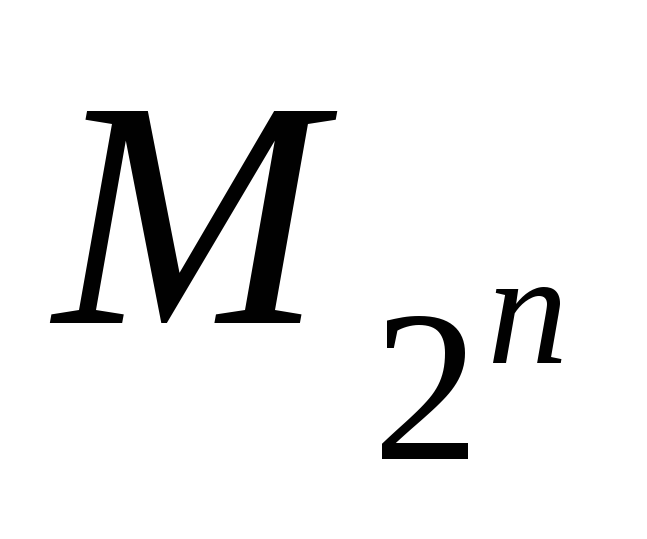 – счетно.
– счетно.Дано множество А=
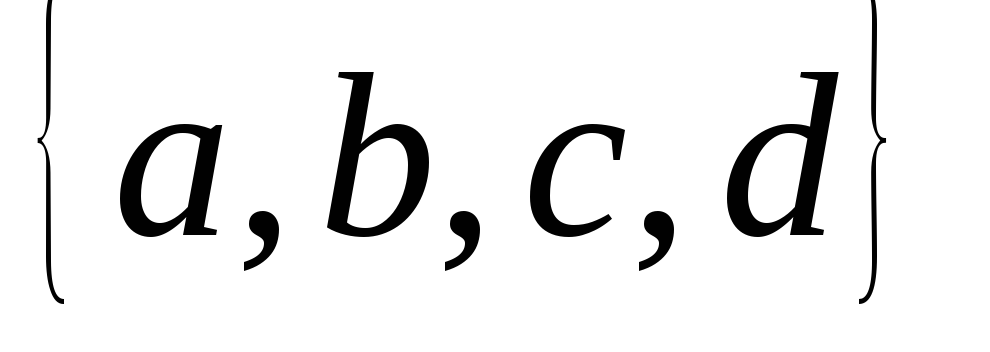 и два преобразования этого множества:
и два преобразования этого множества: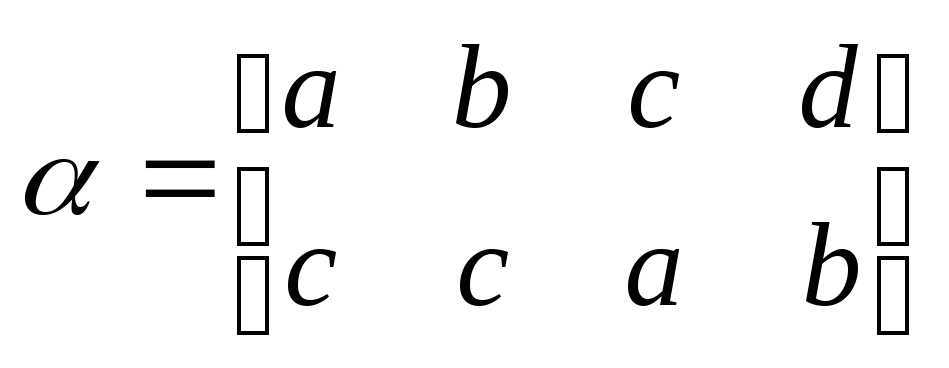 и
и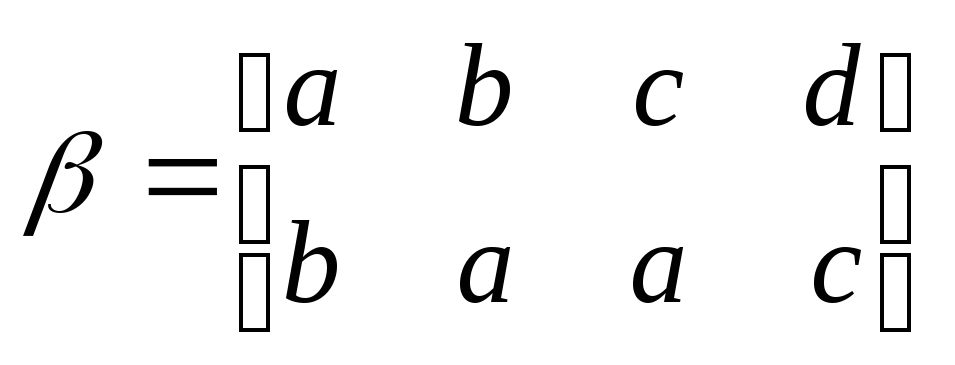 .
Чему равна композиция преобразований?
.
Чему равна композиция преобразований?Какой тип имеет функция
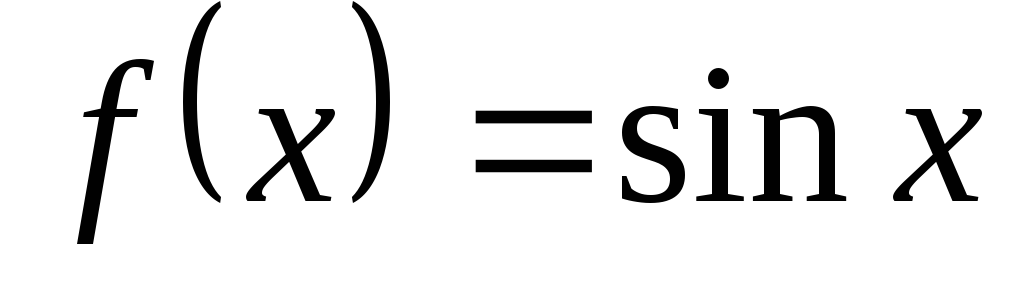 ,
при котором дляfсуществует обратная функцияf
-1?
,
при котором дляfсуществует обратная функцияf
-1?Пусть Х – конечное множество и отображение
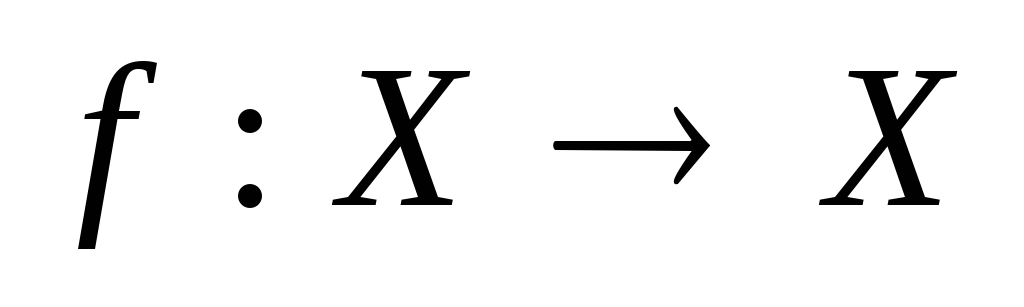 инъективно. Доказать, чтоfбиективно.
инъективно. Доказать, чтоfбиективно.
2.4 Практическое занятие № 9. Операции и их свойства
2.4.1 Теоретические сведения и методические рекомендации по решению задач
Операциейназывают функцию, все
аргументы и значения которой принадлежат
одному и тому же множеству:![]() .
В таких случаях говорят, что множество
Мзамкнутоотносительно операции
.
В таких случаях говорят, что множество
Мзамкнутоотносительно операции![]() ;nназываетсяарностьюоперации.
;nназываетсяарностьюоперации.
При n=1 операция![]() –функция одного аргумента:
–функция одного аргумента:![]() ,
она имеет тип
,
она имеет тип![]() и называетсяунарной операцией.
и называетсяунарной операцией.
При n=2 операция![]() –функция двух аргументов
–функция двух аргументов![]() (
(![]() ),
она имеет тип
),
она имеет тип![]() и называетсябинарной операцией.
и называетсябинарной операцией.
Мультипликативнаятерминология:
операция![]() называетсяумножением, а результат
применения этой операции к элементам
называетсяумножением, а результат
применения этой операции к элементам![]() –произведением
–произведением![]() .
.
Аддитивнаятерминология: операцию
называетсясложением, а результат
ее выполнения –суммой![]() элементоваиb.
элементоваиb.
Бинарная операция![]() называетсякоммутативнойна множествеМтогда и только тогда, когда
называетсякоммутативнойна множествеМтогда и только тогда, когда![]()
![]() .
.
Бинарная операция
![]() называетсяассоциативнойна множествеМтогда и только тогда, когда
называетсяассоциативнойна множествеМтогда и только тогда, когда![]()
![]() (выполнение этого условия означает, что
скобки в выражении
(выполнение этого условия означает, что
скобки в выражении![]() можно
не расставлять).
можно
не расставлять).
Бинарная операция
![]() являетсядистрибутивнойслеваотносительно бинарной операции
являетсядистрибутивнойслеваотносительно бинарной операции![]() на множествеМтогда и только тогда,
когда
на множествеМтогда и только тогда,
когда![]()
![]() .
.
Бинарная операция
![]() являетсядистрибутивнойсправа
относительно бинарной операции
являетсядистрибутивнойсправа
относительно бинарной операции![]() на множествеМтогда и только тогда,
когда
на множествеМтогда и только тогда,
когда![]()
![]() .
.
Бинарная операция
![]() поглощаетбинарную операцию
поглощаетбинарную операцию![]() на множествеМтогда и только тогда,
когда
на множествеМтогда и только тогда,
когда![]()
![]() .
.
Бинарная операция
![]() называетсяидемпотентнойна множествеМтогда и только тогда, когда
называетсяидемпотентнойна множествеМтогда и только тогда, когда![]()
![]() .
.
Нейтральным элементомна множестве
М называется элемент![]() ,
удовлетворяющий условию
,
удовлетворяющий условию![]()
![]() .
.
В мультипликативной терминологии нейтральный элемент называется единицей; в аддитивной терминологии нейтральный элемент называетсянулем.
Симметричнымэлементомдля
элемента![]() называется элемент
называется элемент![]() ,
удовлетворяющий условию
,
удовлетворяющий условию![]() .
.
В мультипликативной терминологии элемент, симметричный элементу аназываетсяобратными обозначаетсяа-1; в аддитивной терминологии нейтральный элемент называетсяпротивоположными обозначается (-а).
