
- •Федеральное агентство по образованию
- •1 Цели и задачи практических занятий по дискретной математике
- •2 Содержание занятий
- •2.1 Практические занятия № 1 – 2. Множества. Операции над множествами. Свойства операций над множествами
- •2.1.1 Теоретические сведения и методические рекомендации по решению задач
- •1) , То есть;
- •2) , То есть.
- •2.1.2 Примеры решения задач
- •2.1.3 Задачи для самостоятельного решения
- •2.2.1 Теоретические сведения и методические рекомендации по решению задач
- •2.2.2 Примеры решения задач
- •2.2.3 Задачи для самостоятельного решения
- •2.3 Практическое занятие № 8. Соответствия и их свойства
- •2.3.1 Теоретические сведения и методические рекомендации по решению задач
- •2.3.2 Примеры решения задач
- •2.3.3 Задачи для самостоятельного решения
- •G1 g2
- •2.4 Практическое занятие № 9. Операции и их свойства
- •2.4.1 Теоретические сведения и методические рекомендации по решению задач
- •2.4.2 Примеры решения задач
- •2.4.3 Задачи для самостоятельного решения
- •2.5 Практическое занятие № 10. Гомоморфизмы
- •2.5.1 Теоретические сведения и методические рекомендации по решению задач
- •2.5.2 Примеры решения задач
- •2.5.3 Задачи для самостоятельного решения
- •2.6 Практическое занятие № 1112. Алгебры с одной бинарной операцией. Полугруппы. Моноиды. Группы. Подгруппы. Циклические группы. Группа подстановок
- •2.6.1 Теоретические сведения и методические рекомендации по решению задач
- •2.6.2 Примеры решения задач
- •2.7 Практические занятия № 13 – 15. Алгебры с двумя бинарными операциями. Кольца. Поля. Решетки. Булевы алгебры
- •2.7.1 Теоретические сведения и методические рекомендации по решению задач
- •2.7.2 Примеры решения задач
- •2.7.3 Задачи для самостоятельного решения
- •2.8 Практические занятия № 16 – 19. Комбинаторика
- •2.8.1 Теоретические сведения и методические рекомендации по решению задач
- •2.8.2 Примеры решения задач
- •2.8.3 Задачи для самостоятельного решения
- •2.9 Практическое занятие № 20. Контрольная работа
- •2.10 Практические занятия № 21 – 22. Орграфы и бинарные отношения. Связность. Компоненты связности
- •2.10.1 Теоретические сведения и методические рекомендации по решению задач
- •2.10.2Примеры решения задач
- •2.10.3 Задачи для самостоятельного решения
- •2.11 Практические занятия № 23 – 25. Поиск путей в графах орграфах. Минимальные пути в нагруженных орграфах. Эйлеровы цепи и циклы. Сети и потоки
- •2.11.1 Теоретические сведения и методические рекомендации по решению задач
- •2.11.2 Примеры решения задач
- •2.11.3 Задачи для самостоятельного решения
- •3 Технические и инструментальные средства
- •4 Порядок проведения занятий
- •Содержание
2.1.2 Примеры решения задач
Задача 1.Доказать и проиллюстрировать
на примере множеств![]() ,
,![]() ,
,![]() тождество алгебры множеств, выражающее
закон ассоциативности операции
пересечения множеств.
тождество алгебры множеств, выражающее
закон ассоциативности операции
пересечения множеств.
Решение. Для доказательства тождества![]() докажем два включения:
докажем два включения:![]() и
и![]() .
.
Пусть
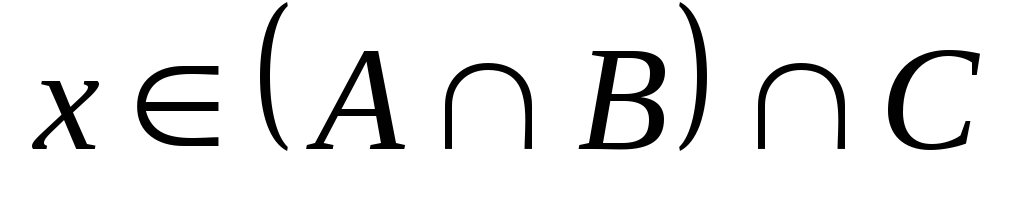 ,
тогда последовательно получаем
,
тогда последовательно получаем
![]()
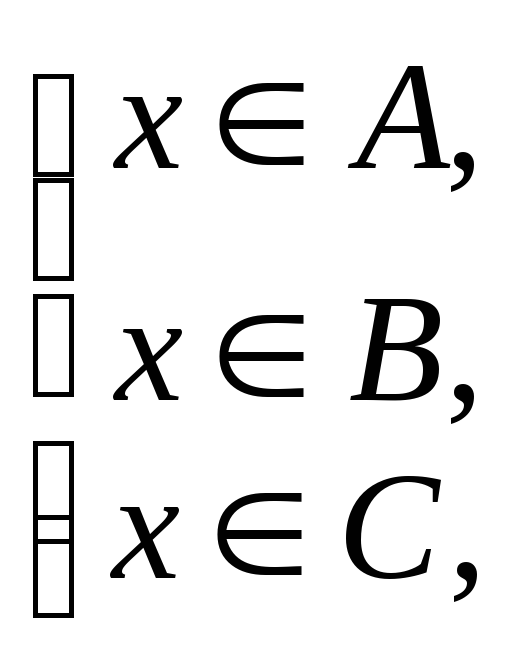
![]()
следовательно,
![]() ;
;
аналогично доказывается второе включение: пусть
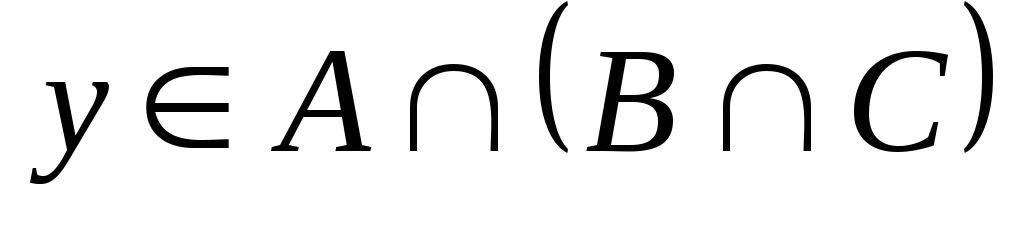 ,
тогда
,
тогда
![]()
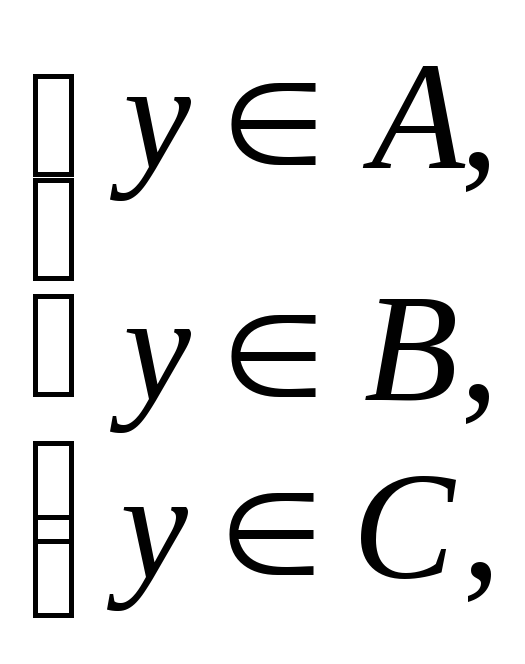
![]()
Окончательно получаем, что
![]() .
.
Тем самым тождество доказано.
Убедимся в верности равенства
![]() на примере данных множеств А, В, С.
Вычислим:
на примере данных множеств А, В, С.
Вычислим:![]() ,
,![]() ;
;![]() ,
,![]() .
Очевидно, что
.
Очевидно, что![]() .
.
Задача 2.Изобразить на координатной
плоскости множества A и В точек
координатной плоскости, удовлетворяющих
соответственно соотношениямx2+y2≤1 иx2+(y-1)2≤1. Какие фигуры изображают множества
AB,![]() ?
?
Решение. Оба множества представляют
собой на плоскости круги с радиусамиR= 1, при этом центр первого круга находится
в точке с координатами (0, 0), а второй –
(0, -1). Фигуры, изображающие множества А,
В, AB,![]() ,
представлены на рисунке 2 (закрашены
темным цветом).
,
представлены на рисунке 2 (закрашены
темным цветом).
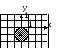
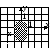
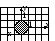
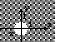
А В AB![]()
Рисунок 2 – Решение задачи 2 (2.1.2)
Задача 3.Доказать, что эквивалентны
три предложения о произвольных множествах
А, В и С: 1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
Решение. Докажем, что из первого
предложения следует второе. Действительно,
так как![]() ,
то осталось показать, что
,
то осталось показать, что![]() .
Но если
.
Но если![]() ,
то
,
то![]() .
В самом деле,
.
В самом деле,![]() .
Следовательно,
.
Следовательно,![]() .
.
Докажем, что из второго предложения
следует третье. Так как
![]() ,
то
,
то![]() .
По закону поглощения
.
По закону поглощения![]() .
Отсюда по закону коммутативности
получаем
.
Отсюда по закону коммутативности
получаем![]() .
.
Докажем теперь, что из третьего предложения
следует первое. Так как
![]() ,
а по условию третьего предложения
,
а по условию третьего предложения![]() ,
то
,
то![]() .
.
2.1.3 Задачи для самостоятельного решения
Какие из приведенных определений множеств являются корректными:
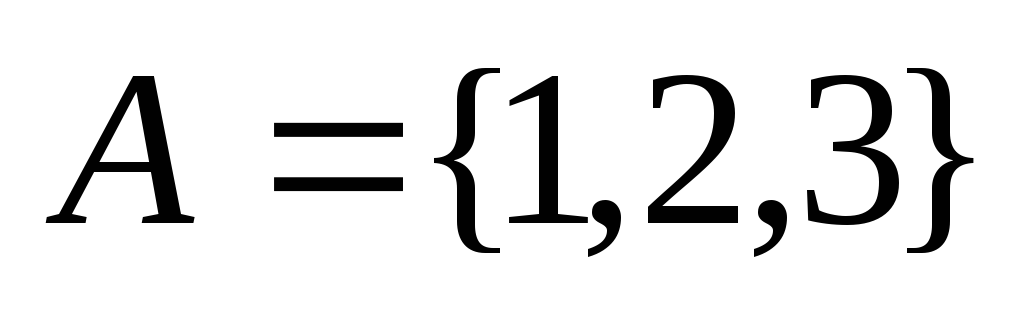 ;
;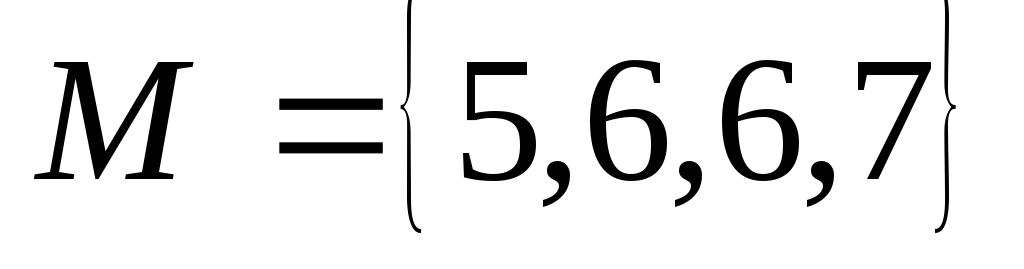 ;
;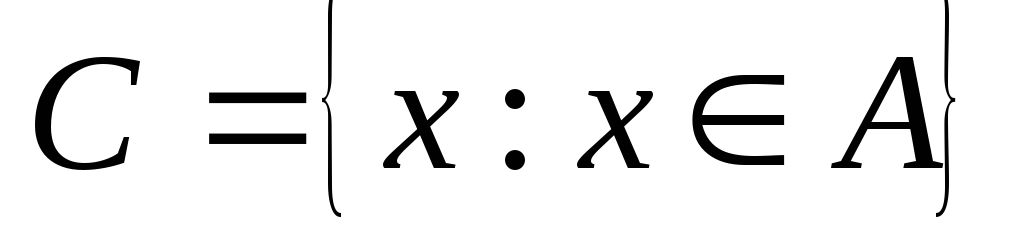 ;
;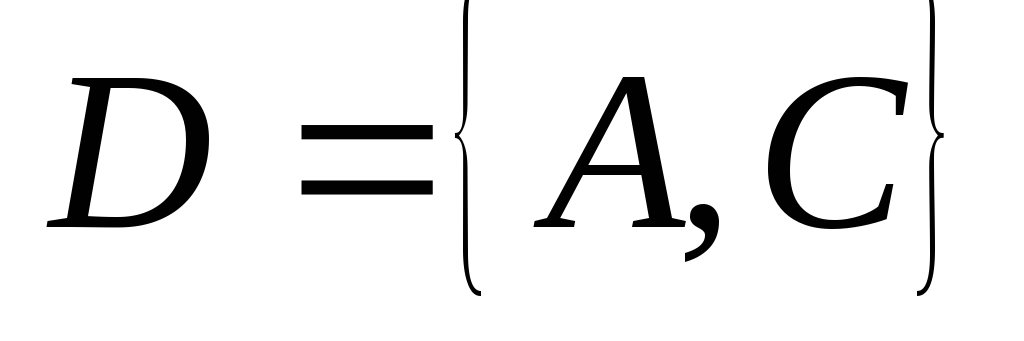 .
Принадлежит ли число 1 множествуD?
.
Принадлежит ли число 1 множествуD?Даны множества Х ={l, 2, 3, 4, 5}, Y = {2, 4, 6, 7}. НайдитеXY,X∩Y,X\Y,Y\Х.
Проиллюстрируйте графически тождества
X(YZ)=(XY)(XZ) ,
X(YZ)=(XY)(XZ) .
Пусть R – множество вещественных чисел, X={x: хR; 0 ≤x≤1},Y={y: уR; 0 ≤y≤2}. Что представляют собой множестваXY,XY,X\Y?
Задать различными способами множество N:а) характеристическим свойством; б) порождающей процедурой.
Задать различными способами множество всех положительных четных чисел 2, 4, 6, …, не превосходящих 100: а) характеристическим свойством; б) порождающей процедурой.
Доказать, что множество Аположительных четных чисел равно множествуВположительных целых чисел, представленных в виде суммы двух положительных нечетных чисел.
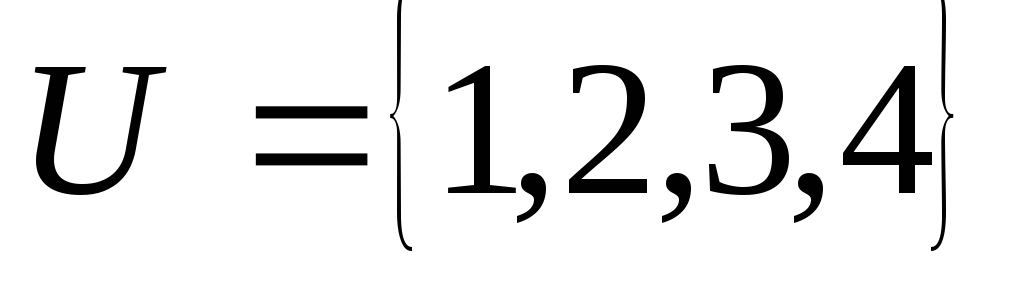 ;
;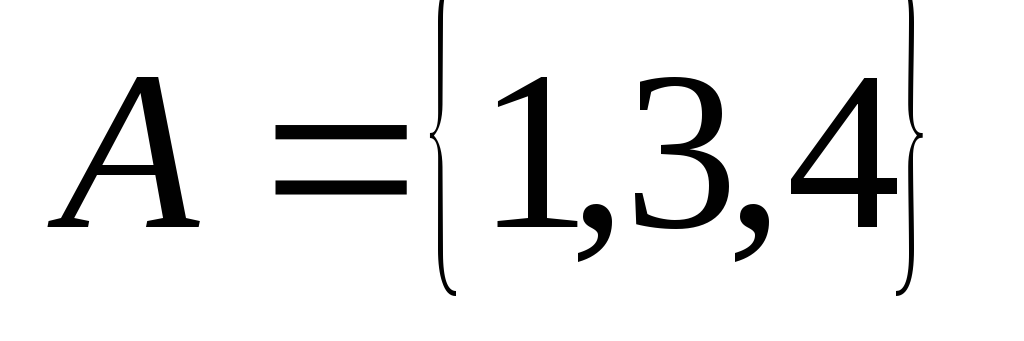 ;
;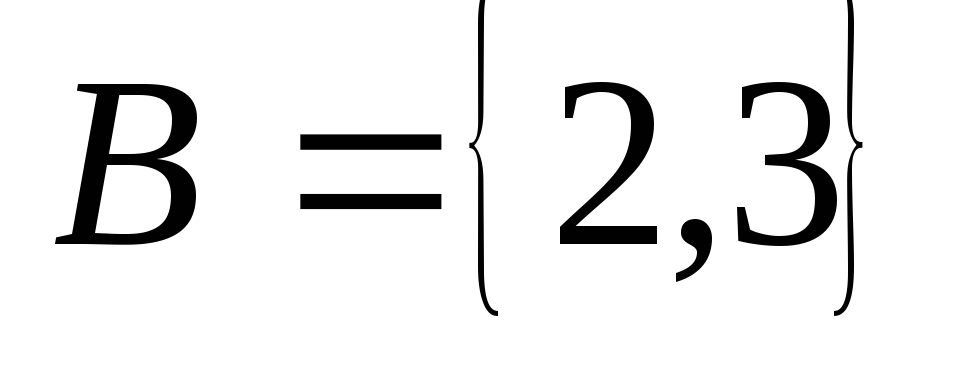 ;
;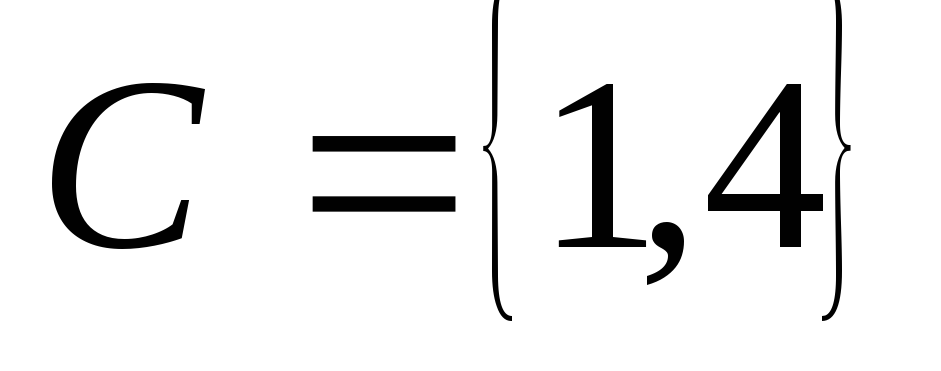 .
Найти
.
Найти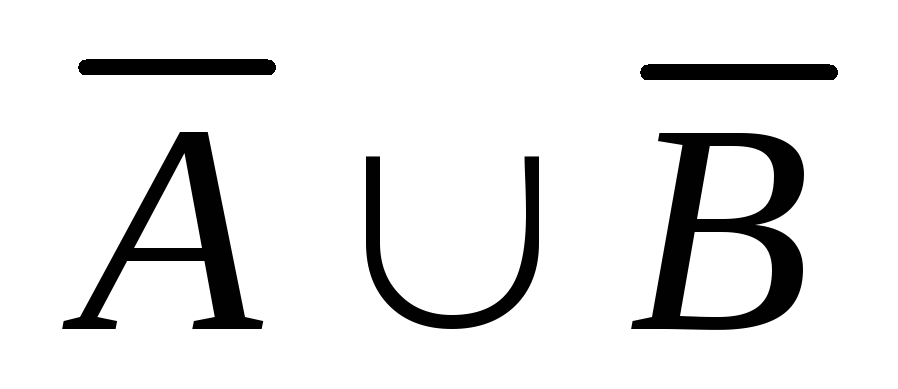 ;
;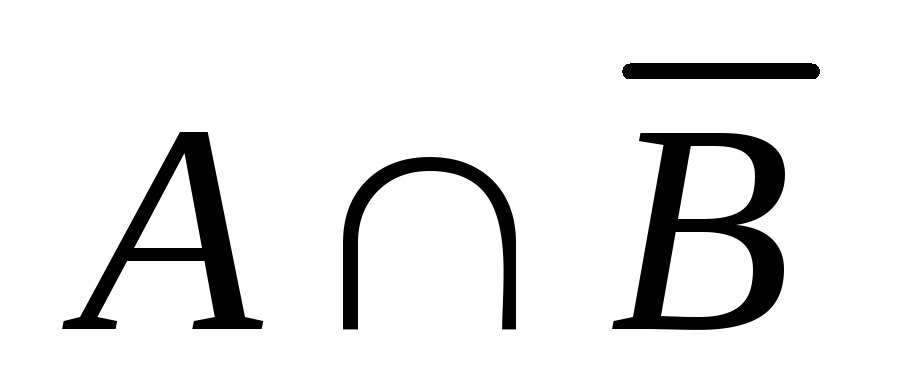 ;
;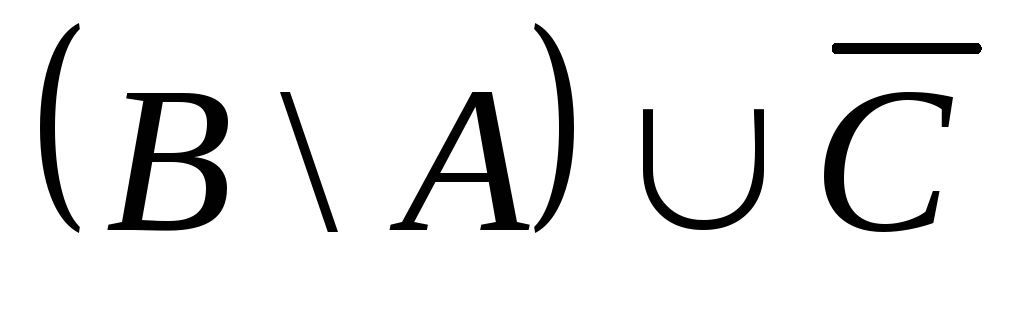 .
.A={1, 2, 3, 4, 5, 6},B={1, 2, 3},C={3, 5, 6, 7, 8}. Найти
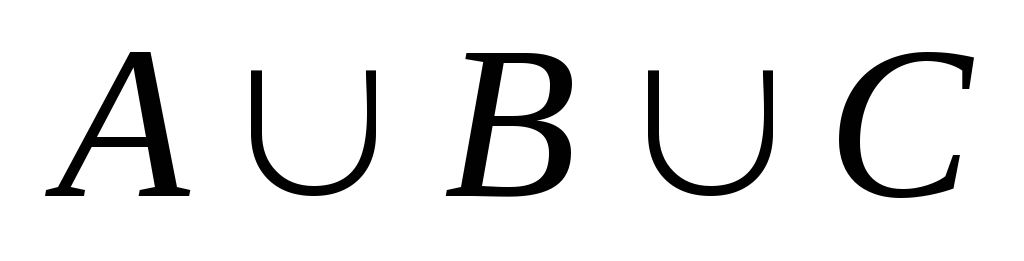 ,
,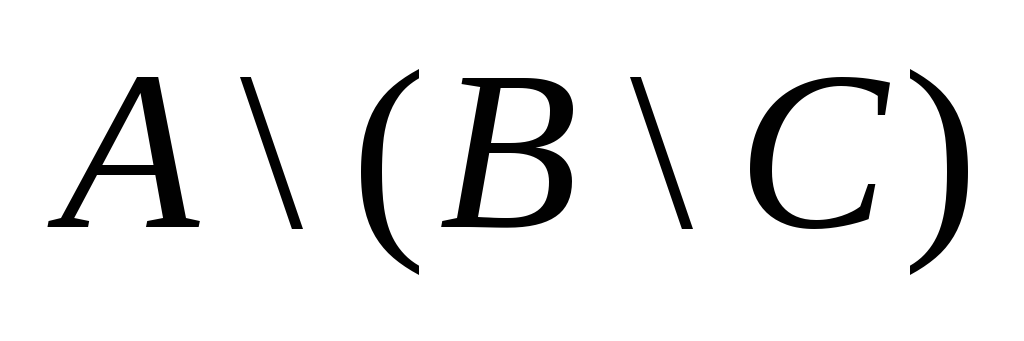 ,
,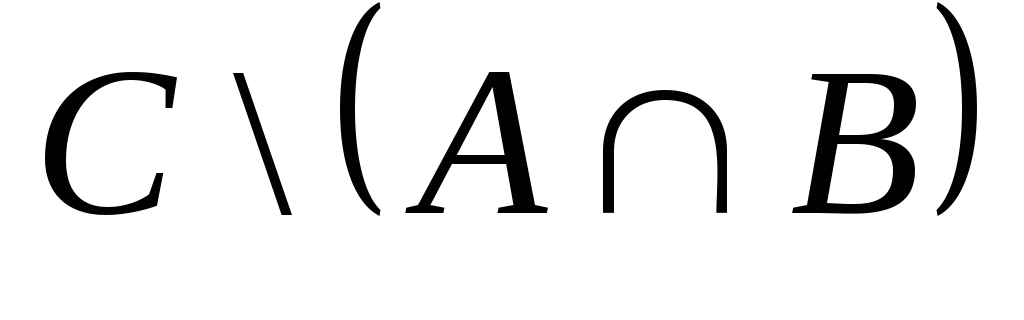 .
.Представить множество
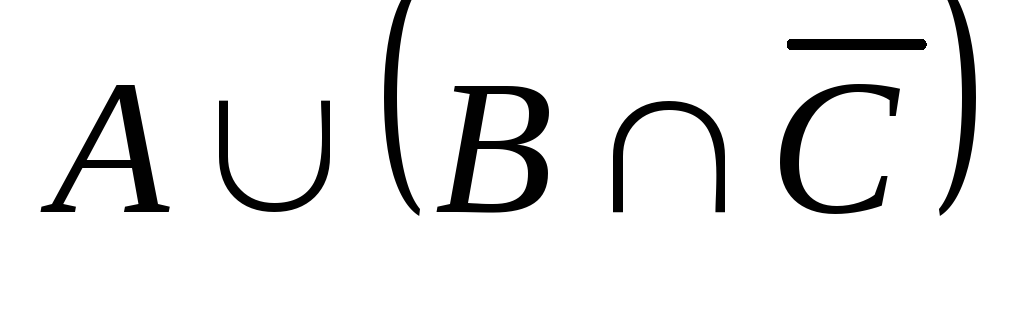 диаграммой Эйлера-Венна.
диаграммой Эйлера-Венна.Проиллюстрировать графически тождества
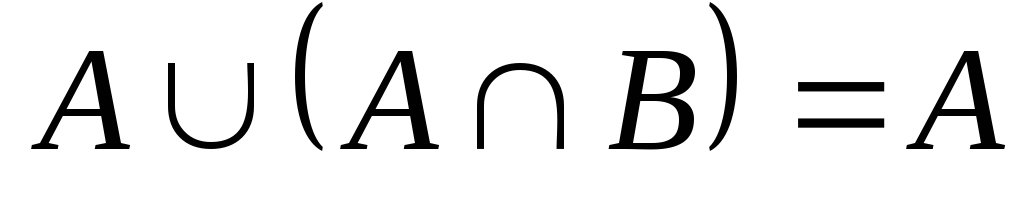 ,
,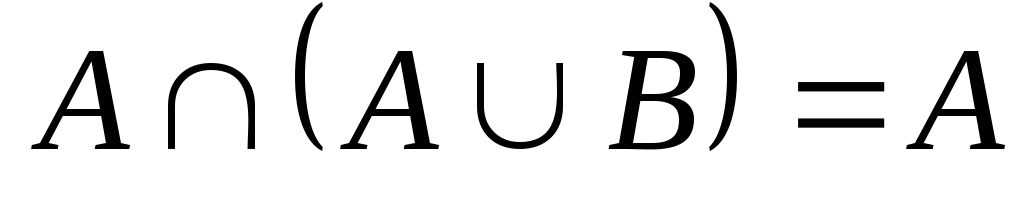 .
.Проиллюстрировать на конкретных примерах, с помощью диаграмм и доказать следующие тождества: а) дистрибутивность пересечения относительно объединения, б) первый закон де Моргана.
Доказать
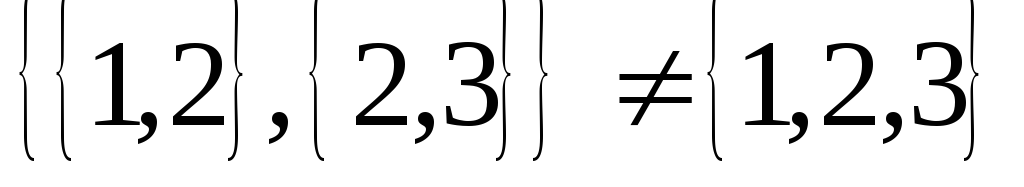 .
.А, ВиС– некоторые множества. Какие из утверждений верны для всех множествА, ВиС:
а) если![]() и
и![]() ,
то
,
то![]() ;
;
б) если
![]() и
и![]() ,
то
,
то![]() Ø;
Ø;
в) если А≠В и В≠С, то А≠С;
г) если![]() и
и![]() ,
то В = Ø?
,
то В = Ø?
Существуют ли такие множества А, ВиС, что
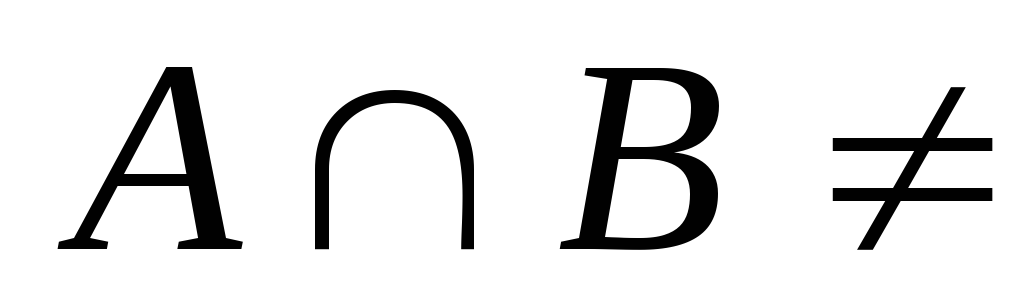 Ø;
Ø;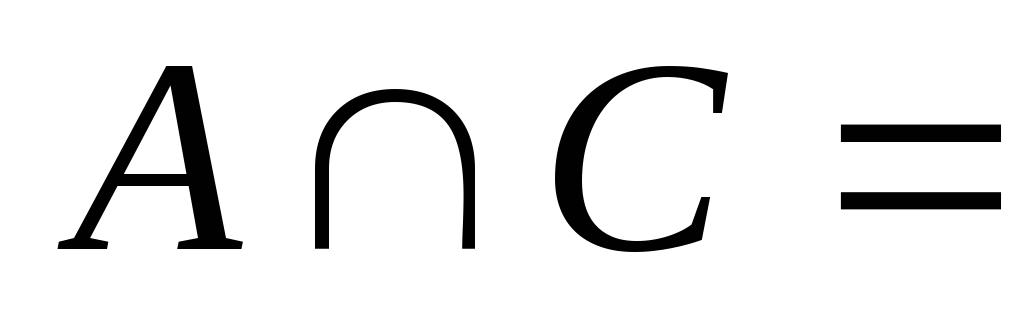 Ø;
Ø;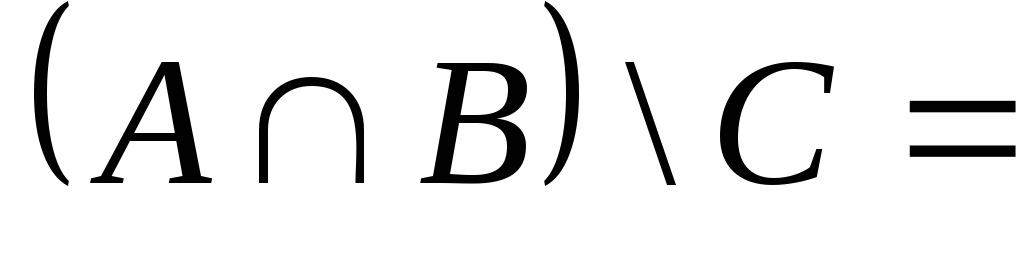 Ø.
Ø.Даны произвольные множества А, Втакие, что
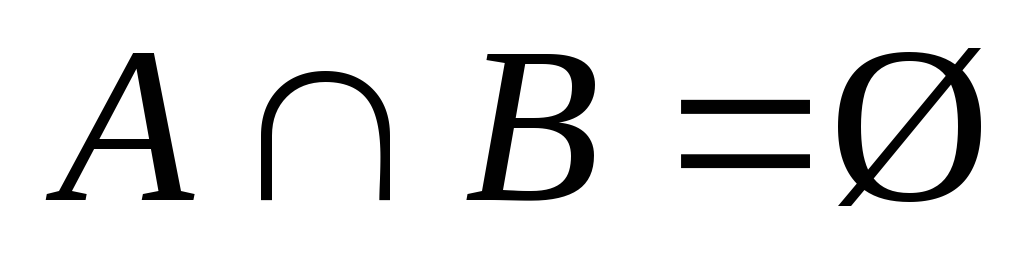 .
Что представляют собой
.
Что представляют собой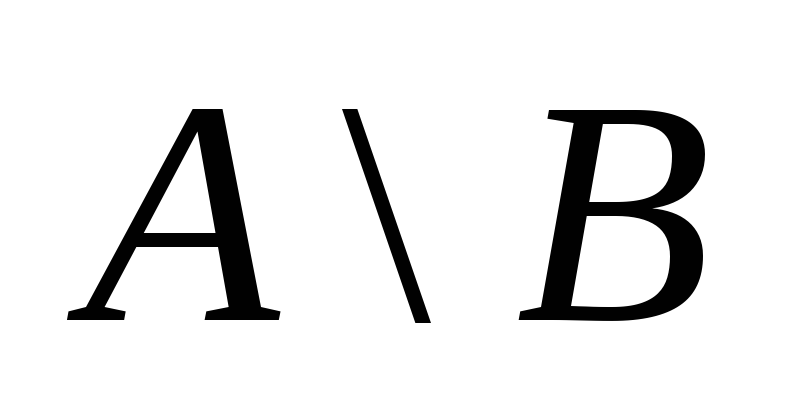 и
и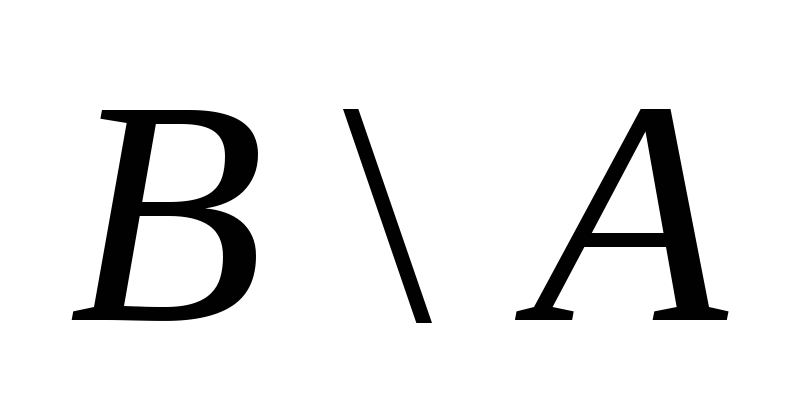 .
.Даны произвольные множества C, Dтакие, что
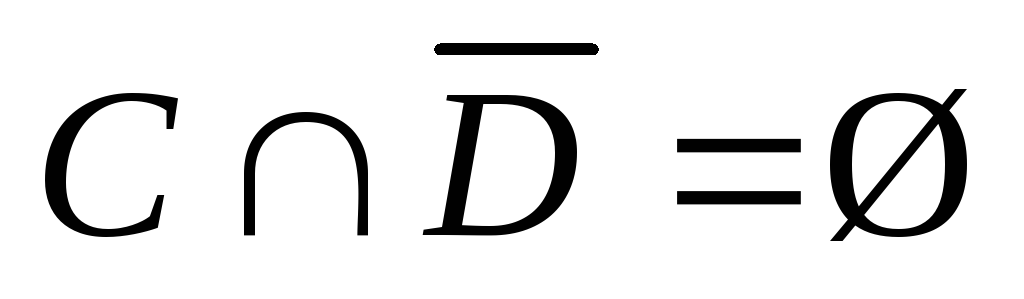 .
Что представляют собой
.
Что представляют собой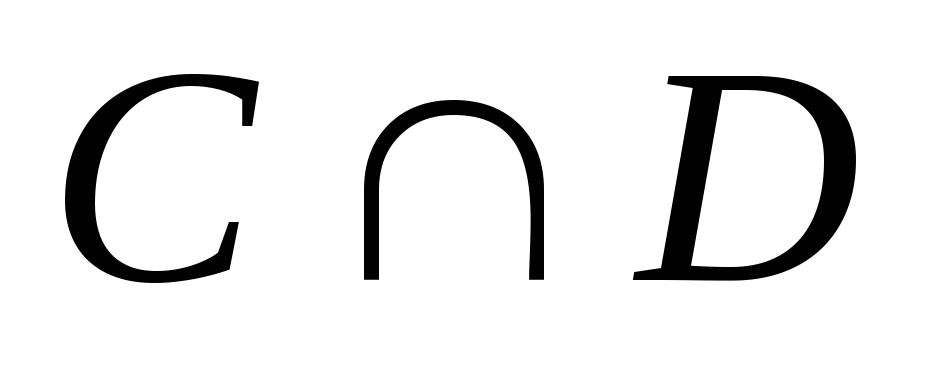 и
и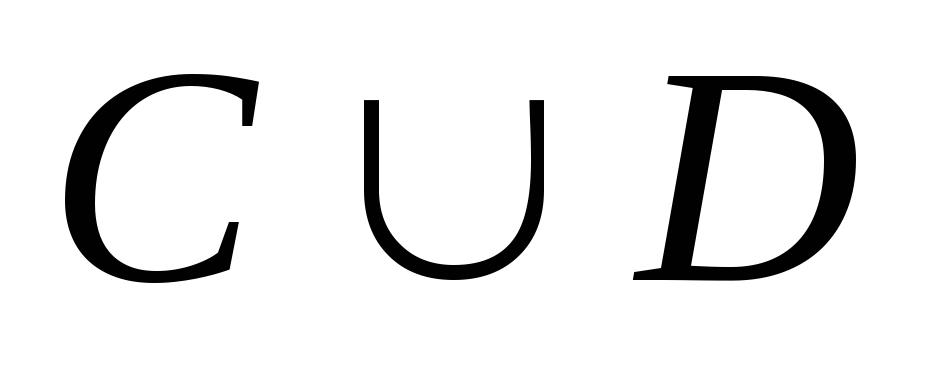 .
.Даны множества А,В иСтакие, что
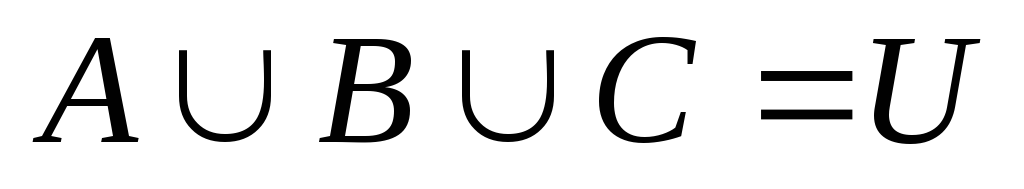 и
и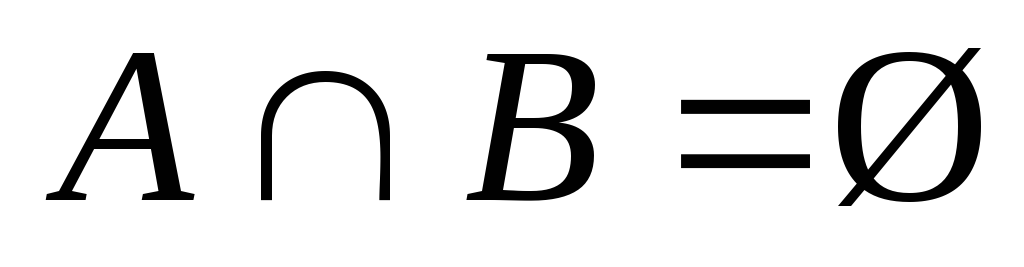 ,
, ,
,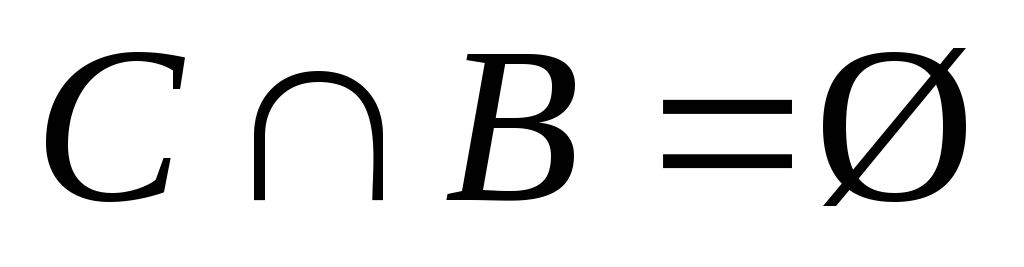 .
Доказать, что
.
Доказать, что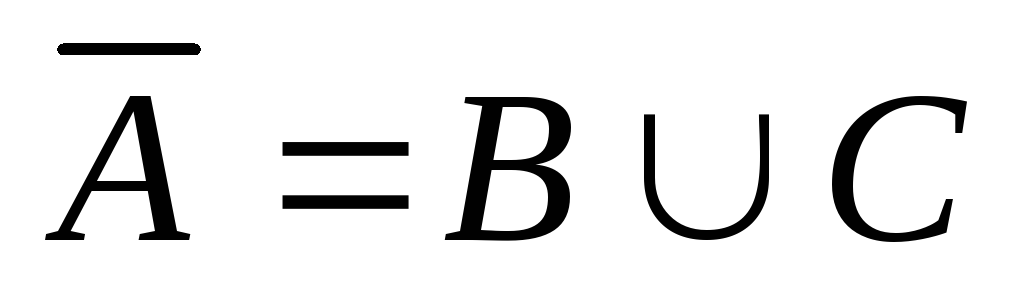 ,
,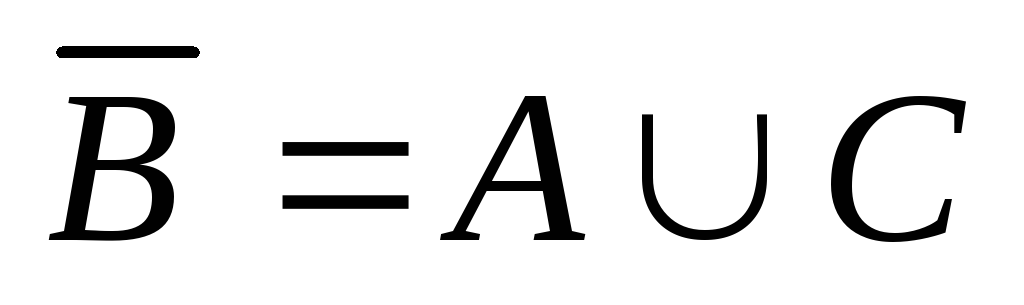 ,
,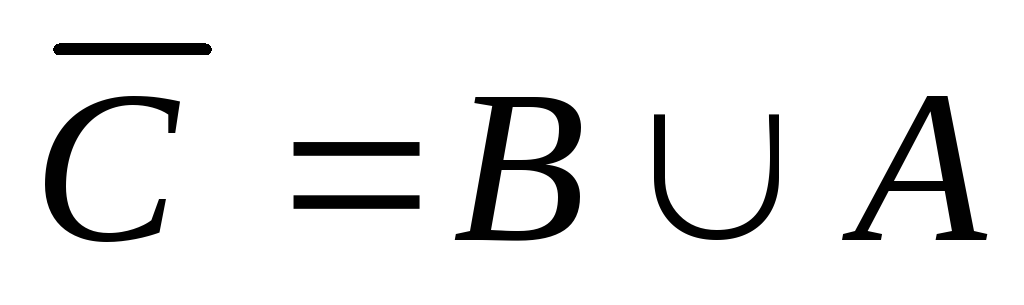 .
.Доказать, что для произвольных множеств А, Вимеет место соотношение
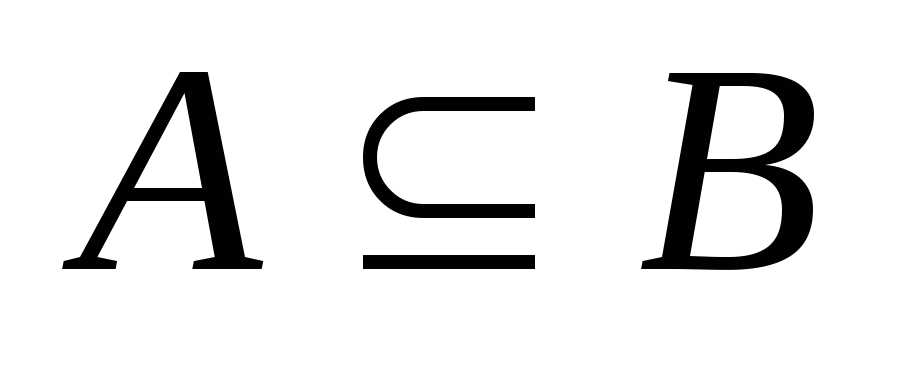 тогда и только тогда, когда
тогда и только тогда, когда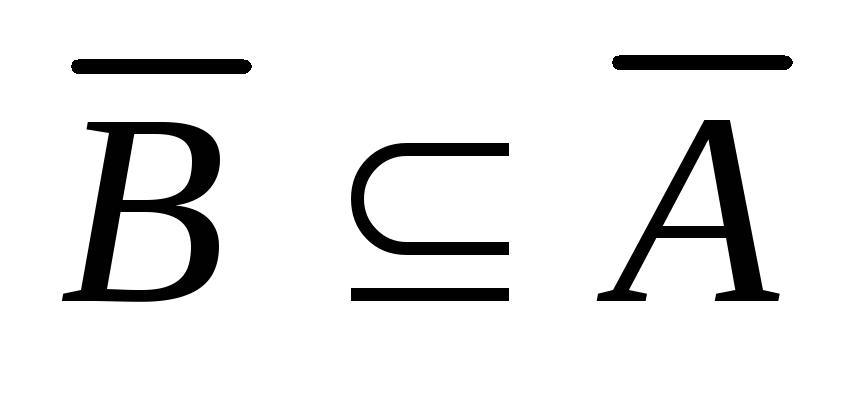 .
.Доказать тождества:
а)![]() ;
;
б)
![]() ;
;
в)
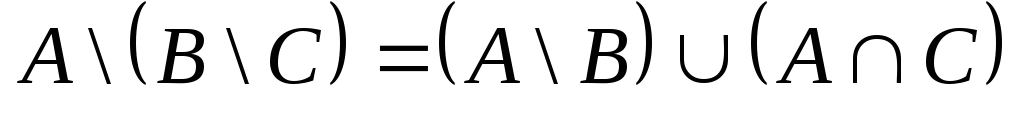 ;
;
г)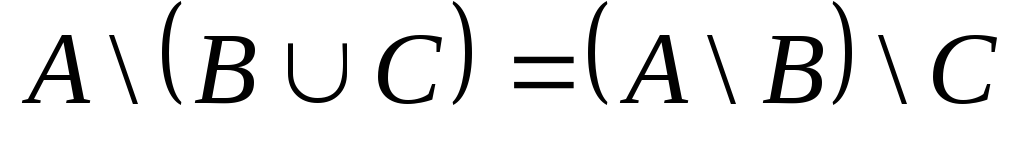 ;
;
д)
![]() ;
;
е)
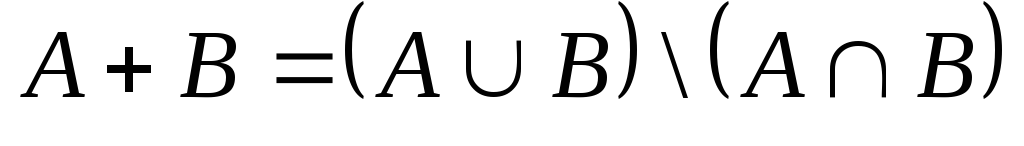 ;
;
ж)
![]() ;
;
з)
![]() .
.
16. Даны множества А,ВиСтакие,
что![]() .
Доказать, что:
.
Доказать, что:
а)
![]() ;
;
б)
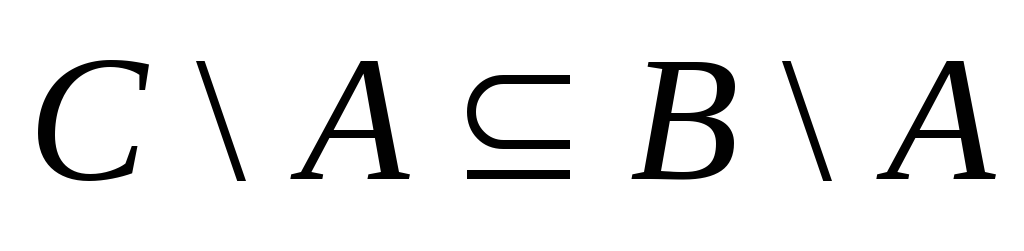 ;
;
в)
![]() .
.
17. Пусть универсум U– конечный, и число элементов в нем не
превосходит размерности ЭВМ. Пронумеруем
элементыU:![]() . ПустьА– подмножествоU,
представимАмашинным словомС,в которомi-ый символ
. ПустьА– подмножествоU,
представимАмашинным словомС,в которомi-ый символ![]() определяется из условия:
определяется из условия:

Аналогично можно представить любое другое подмножество U. Найти объединение, пересечение и дополнение множеств, представленных машинными словами. Проиллюстрировать на примере.
18. Решить систему уравнений
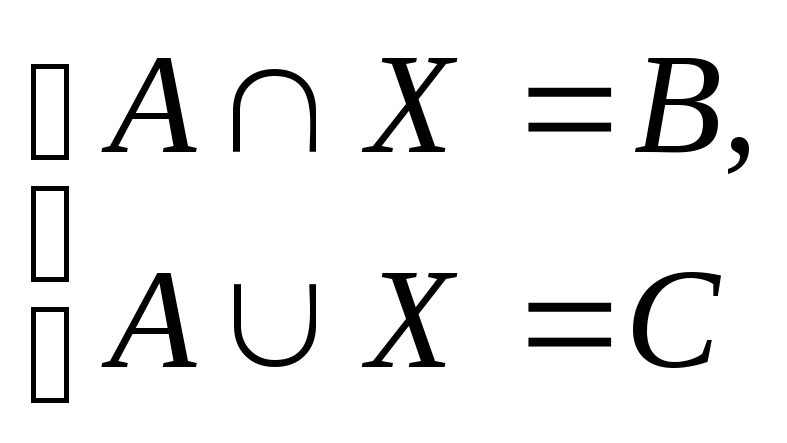
при условии, что
![]() .
.
2.2 Практические занятия № 3 – 7. Бинарные отношения. Способы задания бинарных отношений. Операции над бинарными отношениями. Свойства бинарных отношений. Замыкания бинарных отношений. Отношение эквивалентности. Отношение порядка
