
Lektsiya_3
.docМедичний факультет
Медична і біологічна фізика
Л![]() е к ц і я № 3
е к ц і я № 3
Тема: Основи математичної статистики
План :
-
Генеральна сукупність і вибірка.
-
Характеристика генеральної сукупності і вибірки.
-
Розподіл Стьюдента.
-
Надійний інтервал для генерального середнього.
-
Достовірність різниці генеральних середніх.
-
Поняття функціонального і кореляційного зв’язків.
-
Коефіцієнт кореляції як міра кореляційного зв’язку.
-
Достовірність коефіцієнта кореляції.
-
Рівняння регресії.
-
Поняття множинної кореляції.
Л і т е р а т у р а:
-
Лобоцкая Н.Л. Высшая математика . - Мн.: Выш.шк., 1987.- С. 178-193, 204-215, 217-219.
-
О.П. Минцер, Б.Н.Угаров, В.В.Власов. Методы обработки медицинской информации. К.: «Выща школа», 1991.
-
П.Л.Свердан. Вища математика. Аналіз інформації у фармації та медицині. Львів: «Світ» , 1998. – С. 154-155, 167-178, 209-221.
Математична статистика - розділ прикладної математики, що вивчає методи опису і аналізу експериментальних даних, отриманих в результаті вивчення масових випадкових явищ.
Отримані в результаті спостережень значення випадкової величини складають просту статистичну сукупність або простий статистичний ряд, який підлягає обробці і науковому аналізу.
В загальному, статистична сукупність це множина об’єктів, однорідних відносно деякої якісної або кількісної ознаки, характерної для даних об’єктів.
Якщо сукупність включає всі об’єкти, які можуть бути до неї віднесені, то вона називається генеральною.
З теоретичної точки зору генеральна сукупність є безмежно великою або наближається до нескінченості.
Наприклад, всі хворі гіпертонією, остеохондрозом або іншим захворюванням, які проживають на земній кулі, в певному регіоні або великому місті.
Число об’єктів, що входять в генеральну сукупність, називають її об’ємом і позначають N.
Визначити або дослідити всі об’єкти генеральної сукупності за короткий час неможливо. В зв’язку з цим для дослідження генеральної сукупності відбирають скінчену кількість об’єктів.
Множину об’єктів, випадково відібраних із генеральної сукупності, називають вибіркою.
Число об’єктів вибірки називають її об’ємом і позначають n .
Вибірки за об’ємом поділяють на малі (n 30) і великі (n 30).
Для того, щоб властивості вибірки достатньо повно відображали властивості генеральної сукупності, вибірка повинна бути репрезентативною або представницькою.
Вважається, що вибірка репрезентативна, якщо вона здійснена випадково, тобто при відборі всі елементи генеральної сукупності мали рівну ймовірність попасти у вибірку.
Із одної генеральної сукупності можна здійснити велику кількість виборок. Вибірки поділяють на повторні і безповторні. На практиці користуються здебільшого безповторними вибірками.
Нехай дискретна генеральна сукупність відносно кількісного показника Х має об’єм N. Причому показник Х для об’єктів генеральної сукупності приймає значення х1, х2 , … хn .
Середнє
арифметичне значення показника Х
для генеральної сукупності або
генеральне
середнє позначають
![]() і визначають за співвідношеннями:
і визначають за співвідношеннями:
![]()
де
![]() - ймовірність значення xi
в
генеральній сукупності (і
= 1, 2,
… ,
k); k
- кількість
різних можливих значень дискретного
показника Х.
- ймовірність значення xi
в
генеральній сукупності (і
= 1, 2,
… ,
k); k
- кількість
різних можливих значень дискретного
показника Х.
Висновок:
![]() ,
тобто генеральне середнє
,
тобто генеральне середнє
![]() дорівнює математичному сподіванню μ
випадкової величини Х.
дорівнює математичному сподіванню μ
випадкової величини Х.
На
практиці величина
невідома, її оцінку проводять за допомогою
вибірки. В якості точкової оцінки
приймають середнє арифметичне значення
![]() для вибірки, здійсненої із даної
генеральної сукупності:
для вибірки, здійсненої із даної
генеральної сукупності:
![]() (вибіркове середнє).
(вибіркове середнє).
При
великих
n:
![]() .
.
Для
вибірки розсіювання значень![]() відносно
відносно![]() характеризують вибіркові дисперсія
і середнє квадратичне відхилення:
характеризують вибіркові дисперсія
і середнє квадратичне відхилення:
![]()
![]()
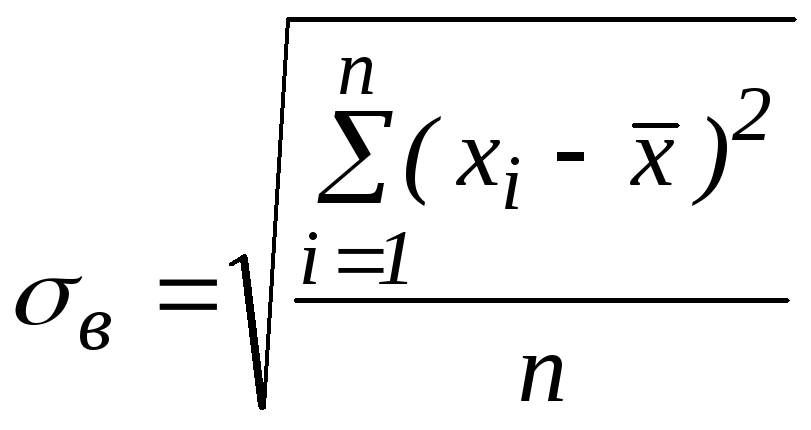 .
.
Генеральна дисперсія:
![]() .
.
Дану величину на практиці визначити неможливо, тому генеральну дисперсію оцінюють за допомогою величини S2:
![]() .
.
Такою
оцінкою генеральної дисперсії користуються
виходячи із малої вибірки (n30).
При великих вибірках (n30)
величини S2
і
![]()
![]() незначно
відрізняються.
незначно
відрізняються.
Оцінка генерального середнього квадратичного відхилення:
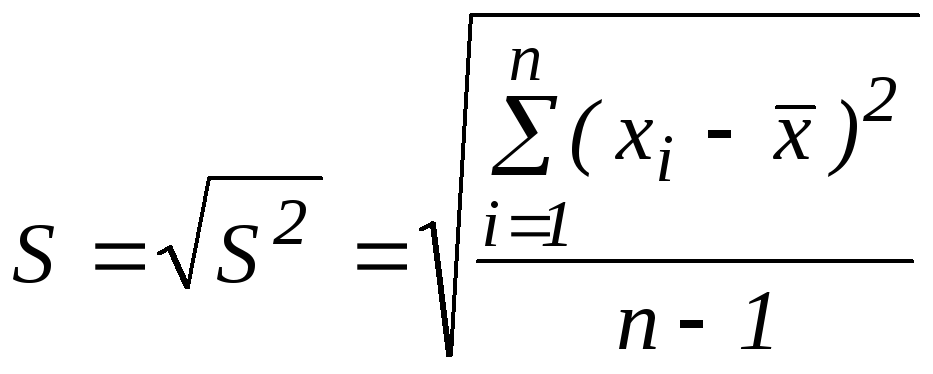 .
.
Вибіркове
середнє
![]() є випадковою величиною. Оцінку середнього
квадратичного відхилення вибіркового
середнього проводять за допомогою
величини
є випадковою величиною. Оцінку середнього
квадратичного відхилення вибіркового
середнього проводять за допомогою
величини
![]() :
:
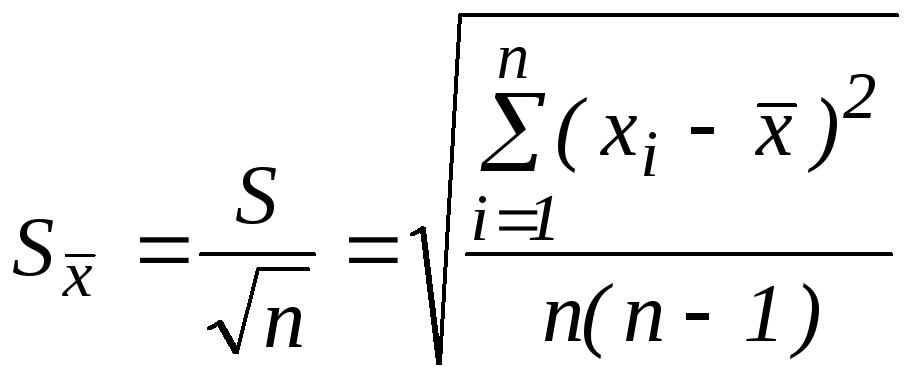 .
.
Дану величину часто називають стандартною похибкою вибіркового середнього і позначають буквою m:
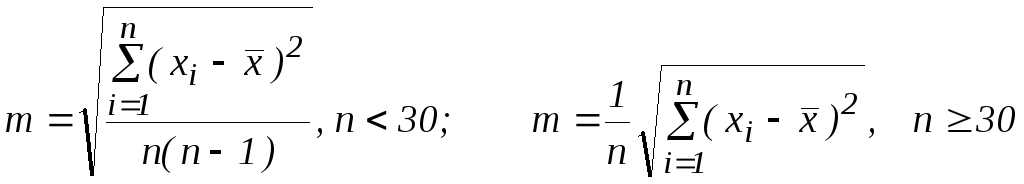 .
.
При знаходженні надійного інтервалу для математичного сподівання величини Х або генерального середнього користуються розподілом Стьюдента. Розподіл Стьюдента базується на понятті нормованого відхилення.
Нормоване відхилення вибіркового середнього від математичного сподівання генеральної сукупності є випадковою величиною:
![]() ,
,
де
![]() -
вибіркове середнє із спостережень;
-
вибіркове середнє із спостережень;
![]() -
середнє
квадратичне відхилення вибіркового
середнього.
-
середнє
квадратичне відхилення вибіркового
середнього.
Числові значення випадкової величини Т позначають t. Розподіл величини Т називається t-розподілом або розподілом Стьюдента.
Густина
ймовірності значень величини Т
виражається формулою:
![]() ,
,
де
n
- об’єм вибірки ;
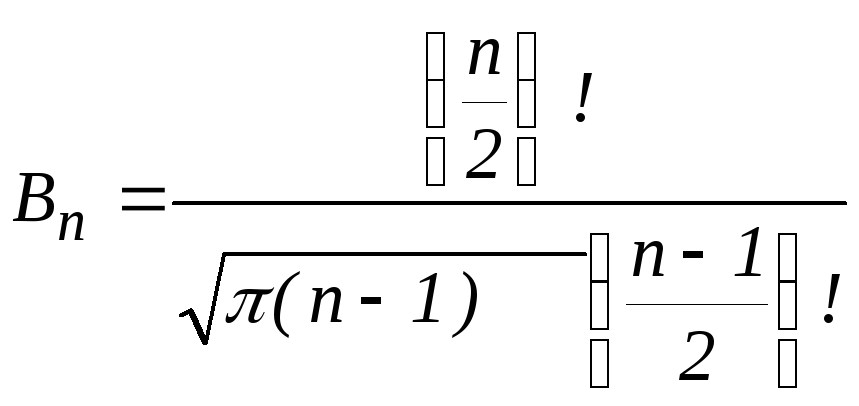 .
.
Г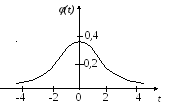 рафік
функції (t)
подібний до кривої нормального розподілу.
рафік
функції (t)
подібний до кривої нормального розподілу.
Із збільшенням об’єму вибірки розподіл Стьюдента наближається до нормального закону розподілу і вже при n 30 практично не відрізняється від нього. Розподілом Стьюдента користуються при малих вибірках n 30.
Використовуючи розподіл Стьюдента можна знайти ймовірність того, що t t0:
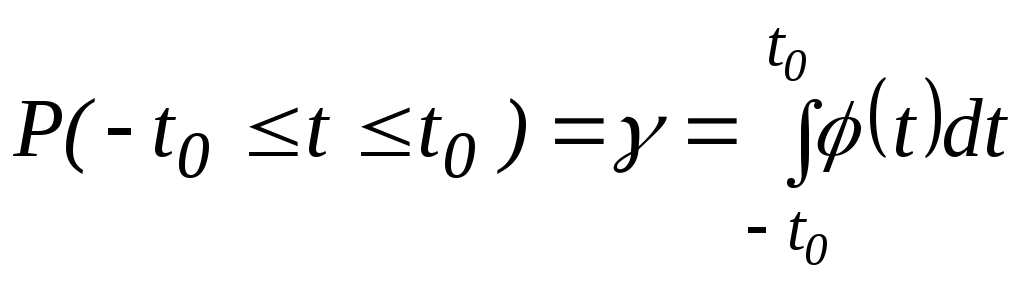 .
.
Або, навпаки, для заданих n і Р можна вказати таке t0, що з ймовірністю Р виконується нерівність:
![]() .
.
В даному виразі t0 називають коефіцієнтом Стьюдента. Його величина залежить від числа степенів вільності = n - 1 і надійної ймовірності , тому його позначають t(). Значення коефіцієнта t() приведені в таблиці (Лобоцька, додаток 4).
Таким
чином
![]() або
або
![]() .
.
Використовуючи спрощені позначення:
![]() ;
;
![]() ,
,
де - математичне сподівання;
![]() -
генеральне середнє;
-
генеральне середнє;
![]() -
вибіркове середнє;
-
вибіркове середнє;
m - середнє квадратичне відхилення вибіркового середнього
(стандартна похибка вибіркового середнього) ;
t - коефіцієнт Стьюдента.
Надійним називають інтервал, в якому з надійною ймовірністю (Р 0,95) знаходиться математичне сподівання генеральної сукупності або генеральне середнє.
Для того, щоб по заданій вибірці: х1, х2, …, хn знайти надійний інтервал, необхідно:
1.
Знайти вибіркове середнє арифметичне:
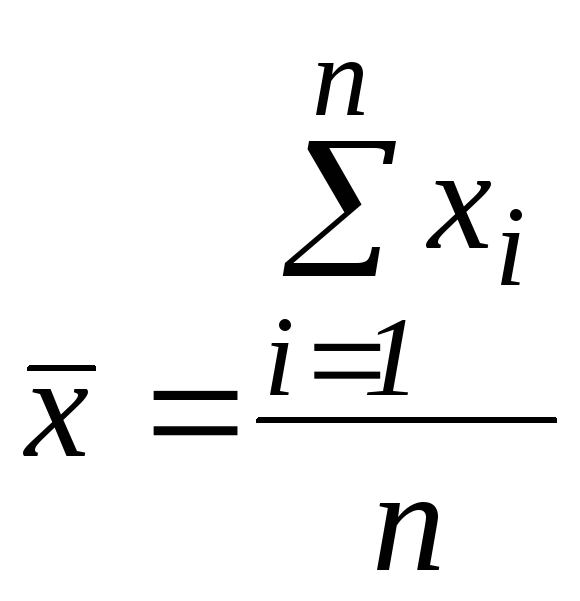 .
.
2. Знайти середнє квадратичне відхилення вибіркового середнього (стандартну похибку):
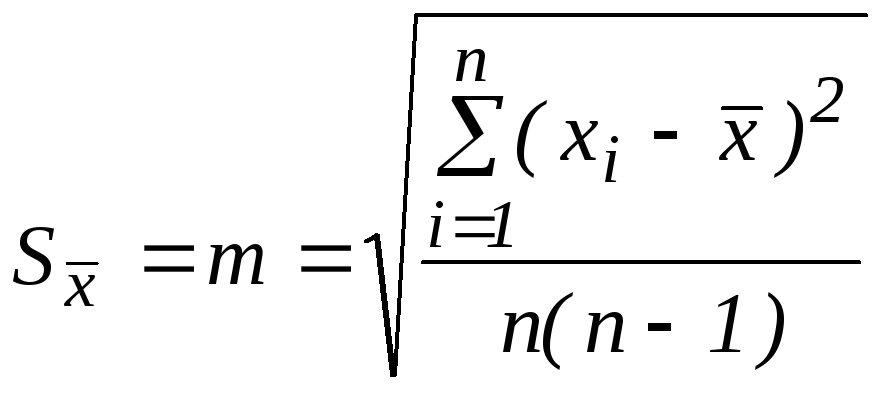 .
.
3. За таблицею розподілу Стьюдента знайти коефіцієнт Стьюдента t = t(f):
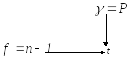
4.
За відомими
![]() записати надійний інтервал:
записати надійний інтервал:
![]() .
.
При
статистичній обробці результатів
медико-біологічних вимірювань часто
виникає потреба оцінки достовірності
різниці генеральних середніх двох
однорідних показників Х
і Y
на підставі різниці вибіркових середніх
даних показників. Тобто відомо, що
![]() З якою ймовірністю можна стверджувати,
що
З якою ймовірністю можна стверджувати,
що
![]()
Будемо вважати, що Х - деякий показник контрольної генеральної сукупності (хворі до лікування), Y - однорідний до X, показник генеральної сукупності, що підлягала впливу природнього або лікувального фактора (хворі після лікування).
Для відповіді на поставлене питання розглядають дві вибірки:
Х:
х1,
х2,…
,
![]() і
Y:
у1,
у2,
…,
і
Y:
у1,
у2,
…,
![]() (ny
може не дорівнювати nx).
(ny
може не дорівнювати nx).
Обчислюють вибіркові середні і їх стандартні похибки:
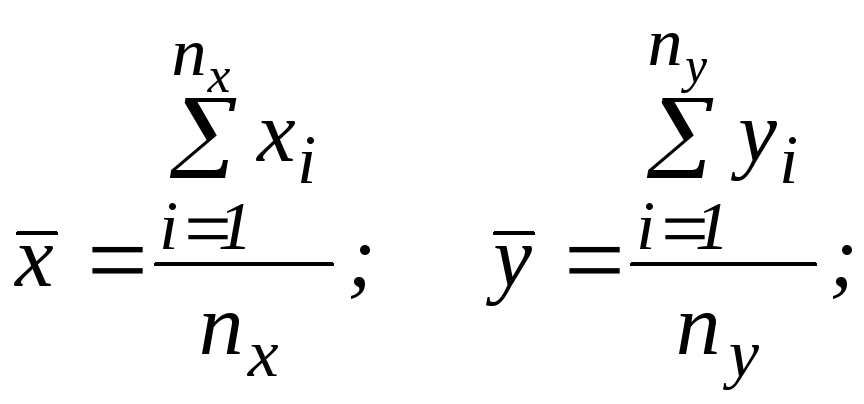
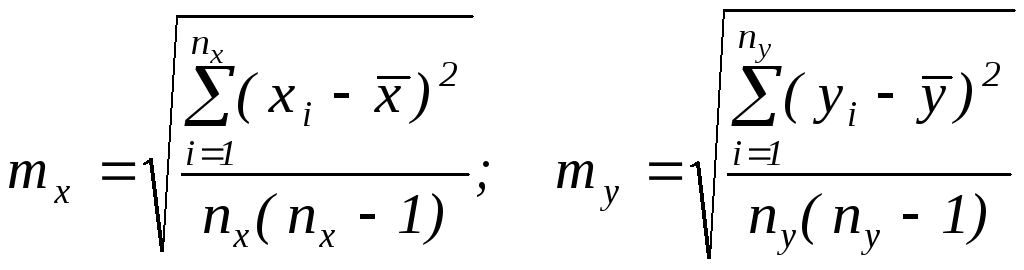 .
.
Оцінку достовірності різниці генеральних середніх проводять за допомогою коефіцієнта Стьюдента:
![]()
![]() .
.
Дану
формулу використовують за умови великих
вибірок, або при
![]() .
.
 Чисельне
значення ймовірності знаходять за
таблицею розподілу Стьюдента:
Чисельне
значення ймовірності знаходять за
таблицею розподілу Стьюдента:
Якщо отримане значення ймовірності Р 0,95, то на підставі різниці вибіркових середніх можна стверджувати, що має місце різниця генеральних середніx. Це означає, що вплив природнього або лікувального фактора призводить до зміни генерального середнього значення показника.
Більш точне і, відповідно, складніше порівняння генеральних середніх двох випадкових величин для великих і малих незалежних вибірок приведені в підручнику Н.Л. Лобоцької “ Высшая математика “ §§ 15.2,15.3 С. 217-219.
Розглянемо основні поняття кореляційного аналізу.
Термін “кореляція” (від лат. correlatio - співвідношення, взаємозв’язок) в математичній статистиці означає ймовірнісну (статистичну) залежність між величинами.
Характер взаємозв’язку між характеристиками явищ може бути як функціональним (однозначним), так і статистичним.
При функціональному зв’язку одному значенню одного показника Х відповідає цілком визначне одне значення іншого показника Y, тобто Y = f(Х).
При статистичній залежності величина Y від величини Х кожному значенню величини Х, із множини її можливих значень , відповідає певний розділ можливих значень величини Y.
При цьому зміна величини Х призводить до зміни розподілу значень величини Y.
Для повного опису статистичного зв’язку між величинами необхідно вказати зв’язок між їх розподілами, що зробити досить складно.
Окремим видом статистичної залежності є кореляційна залежність. При кореляційній залежності між величинами зміна однієї їз них (наприклад, Х) викликає зміну математичного сподівання іншої (Y ).
Прикладом кореляційного зв’язку є зв’язок між ростом і масою людини.
Нехай Х - ріст людини, Y- маса людини.

На практиці для дослідження кореляційного зв’язку між величинами Х і Y здійснюють вибірку об’ємом n.
Нехай для всіх об’єктів вибірки відомі числові значення показників Х і Y.
Об’єкти : 1, 2, 3, …, n
Показники: Х: х1, х2, х3, …, хn
Y: у1, у2, у3, …, уn
Вибіркові середні арифметичні значення показників:
![]() .
.
Вибіркові середні квадратичні відхилення:
![]() .
.
Кількісною мірою кореляційного зв’язку є коефіцієнт кореляції:
![]() .
.
де
![]() нормовані відхилення
нормовані відхилення
![]() і
і
![]() від вибіркових середніх. За
від вибіркових середніх. За
знаком вони можуть бути як додатніми так і від’ємними.
![]()
Тоді
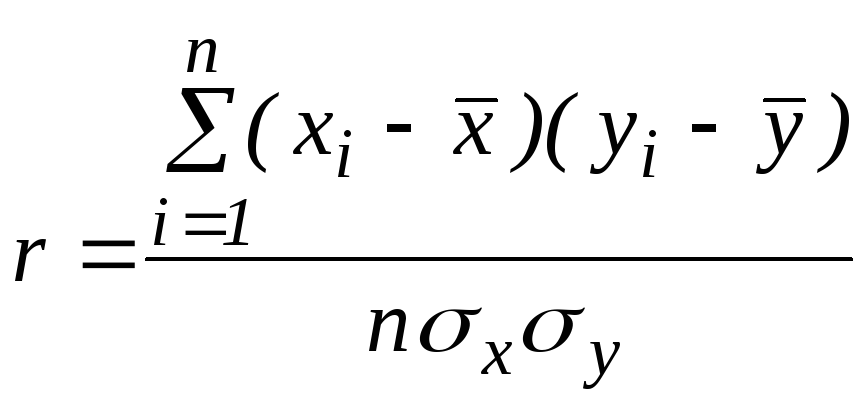 .
З врахуванням виразів для
.
З врахуванням виразів для
![]() і
і
![]() :
:
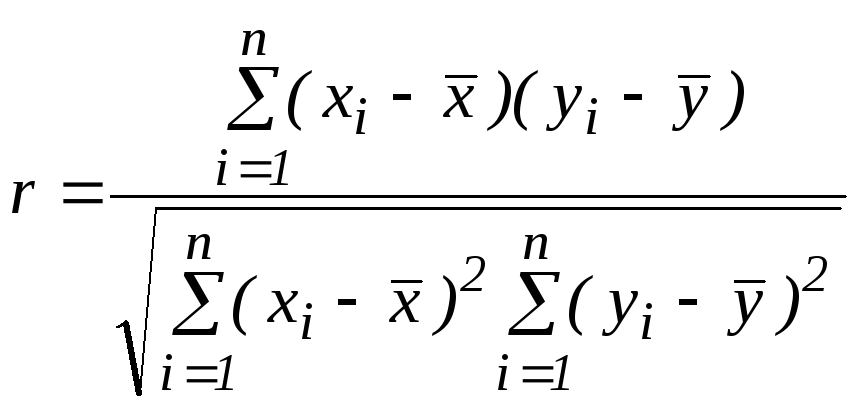 .
.
Використовуючи позначення відхилень:
![]() ,
отримаємо:
,
отримаємо:
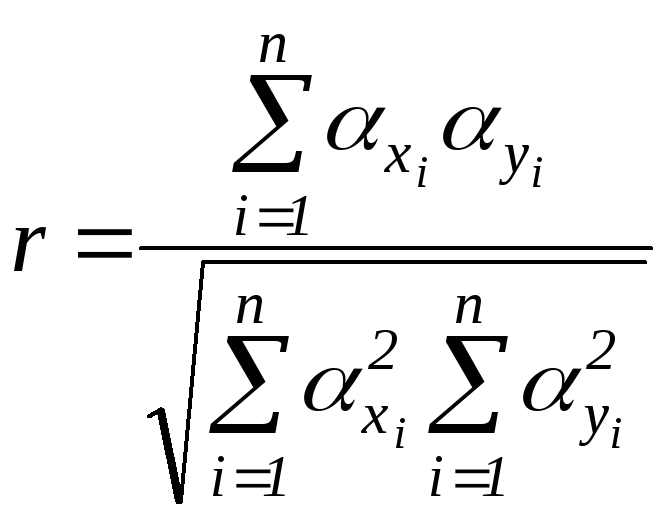 .
.
Властивості коефіцієнта кореляції:
-
-1 r 1 – область можливих значень.
-
Якщо
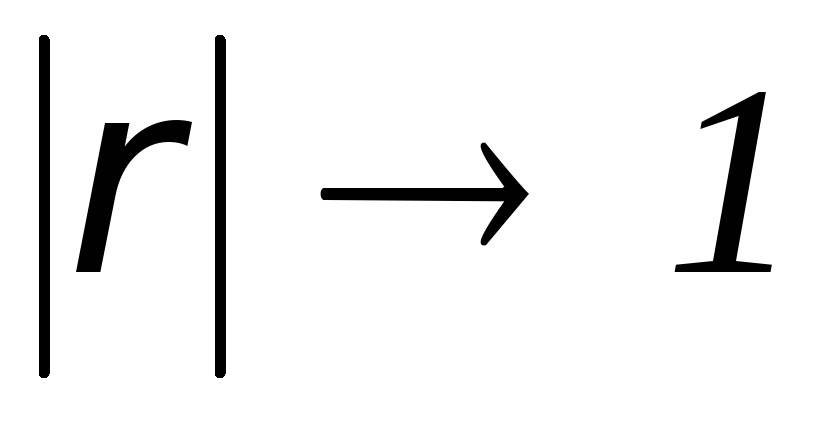 ,
то кореляційний зв’язок
наближається до лінійного функціонального
зв’язку.
,
то кореляційний зв’язок
наближається до лінійного функціонального
зв’язку. -
Якщо
 ,
то кореляційний зв’язок
відсутній.
,
то кореляційний зв’язок
відсутній. -
Якщо 0,7 < r 1, то кореляційний зв’язок сильний або тісний.
-
Якщо 0,5 < r 0,7, то зв’язок середній.
-
Якщо 0 r 0,5, то зв’язок слабкий.
-
Значення r 0 відповідають прямому (додатньому) кореляційному зв’язку, при якому із збільшенням величини одного показника середнє значення іншого також збільшується. Наприклад, із збільшенням росту, маса людей в середньому збільшується; із збільшенням віку, частота гіпертонічних захворювань в середньому зростає.
-
Значення r<0 відповідають зворотньому (від’ємному) кореляційному зв’язку, при якому із збільшенням величини одного показника середнє значення іншого зменьшується.
Для знаходження коефіцієнта кореляції r по заданій вибірці значень показників Х і Y необхідно:
1.
Знайти
![]() i
i
![]() .
.
2. Знайти вибіркові середні:
![]()
3. Знайти всі відхилення :
![]() .
.
4. Знайти квадрати всіх відхилень і суми квадратів:
![]() ,
,
![]()
5. Знайти добутки відхилень і суму добутків:
![]() i
i
![]()
6. За отриманими даними розрахувати коефіцієнт кореляції:
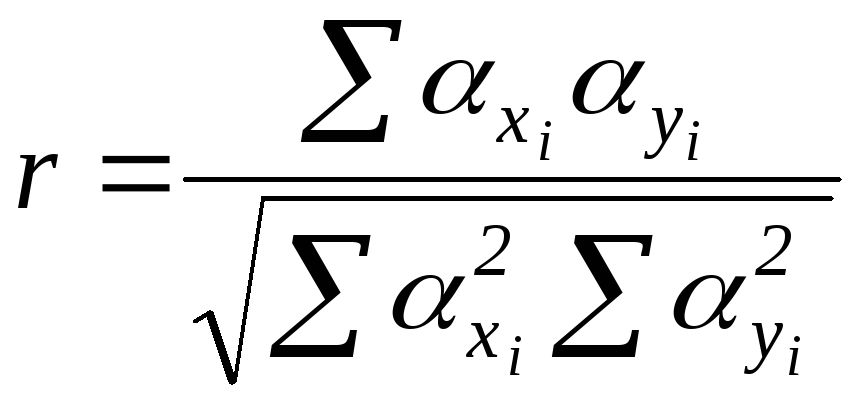 .
.
Розрахунок коефіцієнта кореляції можна звести до заповнення таблиці:
|
№ пп |
хі |
уі |
|
|
|
|
|
|
1 |
5 |
10 |
-1 |
-10 |
1 |
100 |
10 |
|
2 |
8 |
35 |
2 |
15 |
4 |
225 |
30 |
|
3 |
7 |
20 |
1 |
0 |
1 |
0 |
0 |
|
4 |
6 |
20 |
0 |
0 |
0 |
0 |
0 |
|
5 |
4 |
15 |
-2 |
-5 |
4 |
25 |
10 |
|
Σ |
30 |
100 |
0 |
0 |
10 |
350 |
50 |
|
|
х = 6 |
у =20 |
|
|
В |
С |
А |
![]() -
між
показниками Х
і Y
тісний, прямий кореляційний зв’язок.
-
між
показниками Х
і Y
тісний, прямий кореляційний зв’язок.
Приклади числених значень r і їх тлумачення:
r= - 0,62 – середній, зворотній кореляційний зв’язок;
r= 1,12 – помилка при розрахунках, оскільки завжди r1.
На практиці коефіцієнт кореляції визначається для однієї із можливих вибірок і тим самим його чисельне значення є випадковою величиною. Тому перед узагальненням отриманого результата на генеральну сукупність проводять оцінку достовірності коефіцієнта кореляції.
Для оцінки достовірності коефіцієнта кореляції використовують z-перетворення Фішера:
z
=
![]() .
.
Так як r випадкова величина, то і z є також випадковою величиною. На відміну від r величина z підпорядковується нормальному закону розподілу.
Оцінка достовірності проводиться за допомогою коефіцієнта Стьюдента:
![]() ,
,
де
![]() - стандартна
похибка для випадкової величини z.
- стандартна
похибка для випадкової величини z.
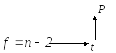 Використовуючи
таблицю розподілу Стьюдента за величиною
t
знаходять
рівень достовірності Р
(або рівень значності р=1-Р)
за кількістю степенів вільності f
= n
– 2:
Використовуючи
таблицю розподілу Стьюдента за величиною
t
знаходять
рівень достовірності Р
(або рівень значності р=1-Р)
за кількістю степенів вільності f
= n
– 2:
Розглянемо елементи регресійного аналізу.
Якщо для генеральної сукупності нанести на координату площину ХОY відповідно пари значень показників Х і Y, то отримаємо так зване кореляційне поле.
Основним завданням в регресійному аналізі є пошук найкращої лінії, що проходить через множину точок кореляційного поля і забезпечує мінімальну суму квадратів відхилень всіх точок від даної лінії.

Графік
функції
![]() називається
лінією регресії у
по х.
Аналогічно можна розглядати регресію
х
по у
називається
лінією регресії у
по х.
Аналогічно можна розглядати регресію
х
по у
![]() .
.
В залежності від виду рівнянь регресії і форми відповідних ліній регресії, говорять про лінійну, квадратичну, експоненціальну і інші форми кореляційної залежності або регресії.
х b
• •



![]()

![]()
![]()
![]()
![]()
Розглянемо випадок лінійної регресії.
![]() ;
;
![]() де
де
![]() .
.
де
![]()
![]() коефіцієнт
регресії у
по
х:
коефіцієнт
регресії у
по
х:
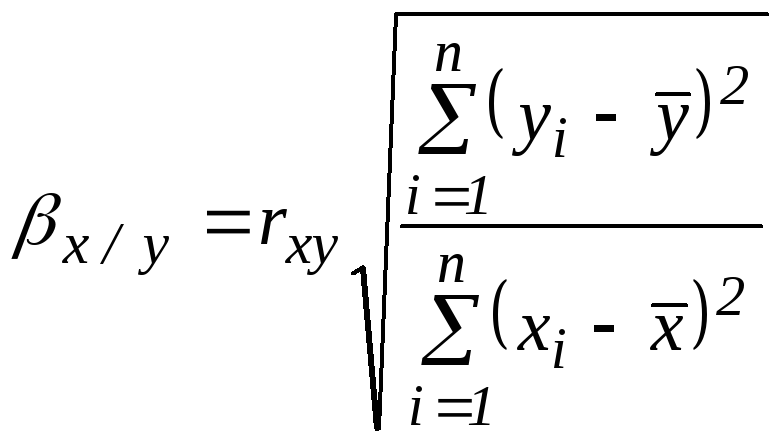 .
.
Рівняння регресії дає можливість оцінити середнє арифметичне значення показника Y для генеральної сукупності по заданому значенню показника Х.
З’ясуємо зміст коефіцієнта регресії у по х:
![]()
![]() .
.
![]()
![]() при
при
![]()
Аналогічно для регресії х по у:
![]() де
де
![]()
![]()
![]() при
при
![]()
