
Начертательная геометрия
.pdf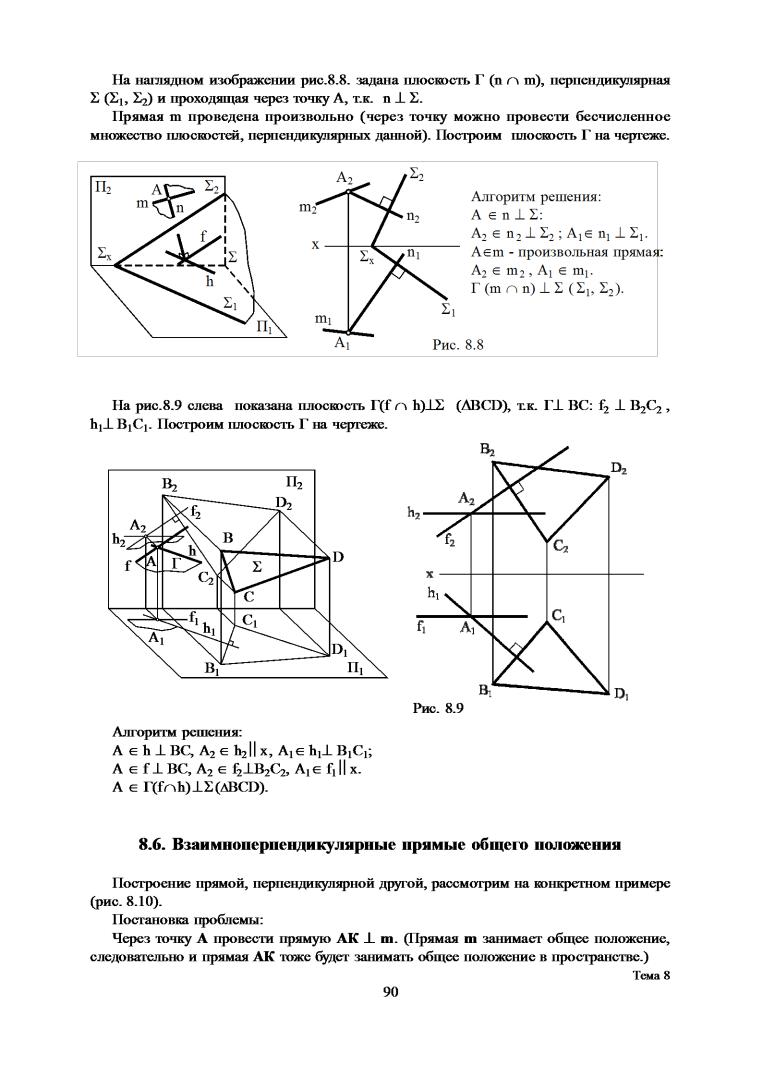
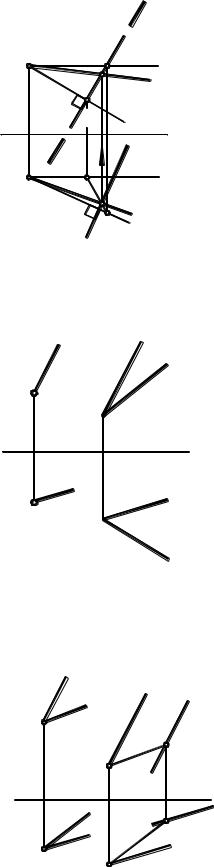
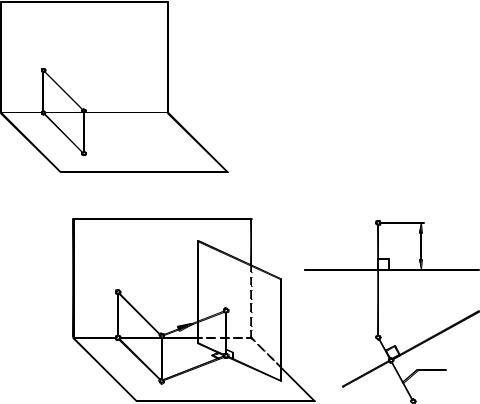
Рис. 8.10 |
Алгоритм решения:
A (f h) m:
A2 f2 m2 , A2 h2 x; A1 h1 m1, A1 f1 x. K = m:
m = ( 2) П2 , m2 = . = 12, 1 h, 2 f.
1222 = m2;
11 h1, 21 f1, 11 21 = 1121; 1121 m1 = K1;
K2 m2.
A2 K2 = A2K2 , A1 K1 = A1K1.
AK m.
8.7. Параллельность прямой и плоскости
Из начального курса геометрии известно, что прямая параллельна плоскости, если она параллельна какой-либо прямой этой плоскости. Чтобы на чертеже провести
|
a2 |
|
A2 |
m2 |
|
b2 |
||
|
x
m1 |
a1 |
|
|
A1 |
|
Рис. 8.11 |
b1 |
прямую, параллельную данной плоскости, достаточно провести произвольную прямую, параллельную любой прямой этой плоскости.
На рис.8.11. проведем через точку А прямую m, параллельную плоскости (a b).
Алгоритм решения:
A m a,
A2 m2 a2, A1 m1 a1.
8.8. Параллельность двух плоскостей
Известно, что плоскости называются параллельными, если две пересекающиеся
прямые одной плоскости параллельны двум пересекающимся прямым второй
плоскости.
Пусть задана плоскость (a | | b), требуется через точку А провести плоскость Г | |
(рис.8.12).
Рис. 8.12 |
Алгоритм решения:
с (a b), с2 = 1222(произвольно),
11 a1, 21 b1, 11 21 =1121 = с1.
A2 a2' a2 , A2 с2' с2 ; A1 a1' a1, A1 с1' с1 . Г (a' с') (a b).
Тема 8
91
Приложение
Любая задача начертательной геометрии сводится к построению искомых фигур (точек, линий, поверхностей, ...), удовлетворяющих определенным позиционным или метрическим условиям. Каждому метрическому условию в пространстве соответствует множество фигур, которые образуют геометрические места (г.м.) точек, прямых и т.д.
Большинство метрических условий сводится к следующим:
–расстояние;
–угол;
–равноудаленность;
–равнонаклоненность.
Перечислим определения наиболее часто встречающихся в пространстве геометрических мест:
1.Геометрическое место точек, удаленных от данной точки О на расстояние R, есть сфера Ф(О,R) - рис. 4.3.
2.Геометрическое место точек, удаленных от данной прямой j на расстояние R, есть поверхность цилиндра вращения Ф (j,R) - рис. 4.9.
3.Геометрическое место точек, удаленных от данной плоскости Г на расстояние d, образует две плоскости Г', Г'', параллельные Г.
4.Геометрическое место прямых, составляющих с данной прямой j угол , это множество прямых, параллельных поверхности конуса вращения Ф (j, ) - рис.4.8.
5.Геометрическое место прямых, составляющих с данной плоскостью Г угол , это множество прямых, параллельных поверхности конуса вращения Ф(j, 900 – ), где j Г - рис. 4.8.
6.Геометрическое место точек, равноудаленных от двух данных точек А, В, есть срединная плоскость, перпендикулярная АВ.
7.Геометрическое место точек, равноудаленных от двух прямых а, b, есть:
–две биссекторные плоскости, если прямые а, b пересекающиеся;
–срединная плоскость, если прямые а, b параллельные.
8. Геометрическое место точек, равноудаленных от плоскостей , есть:
–срединная плоскость, если ;
–две биссекторные плоскости, если .
Вопросы для самоконтроля и задачи для самостоятельной работы по теме "Алгоритмы решения метрических задач"
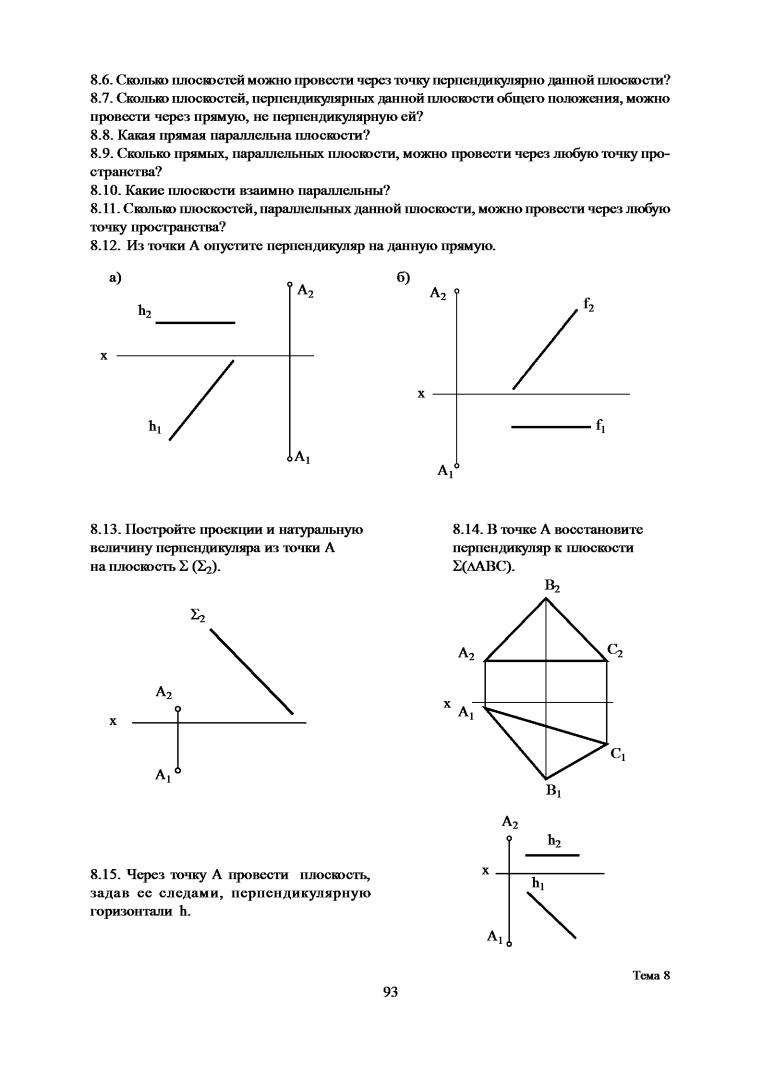
8.1.Какие задачи называются метрическими?
8.2.Как определить натуральную величину отрезка прямой общего положения и углы наклона его к плоскости П1, к плоскости П2 способом прямоугольного треугольника?
8.3.На какую плоскость проекций прямой угол проецируется без искажения, если одна его сторона является горизонталью? Фронталью?
8.4.Условие перпендикулярности прямой и плоскости.
8.5.К чему сводится построение взаимноперпендикулярных плоскостей общего положения?
Тема 8
92
8.16. Постройте плоскость, для которой |
|
8.17. Проверьте перпендикулярность |
|||||
прямая а является линией наибольшего |
|
прямой l |
и плоскости ( АВС). |
||||
наклона к горизонтальной плоскости |
|
|
B2 |
l |
|||
проекций, запишите определитель этой |
|
|
|
||||
|
|
|
|
||||
плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
C2 |
a2 |
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
l1 |
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
a1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
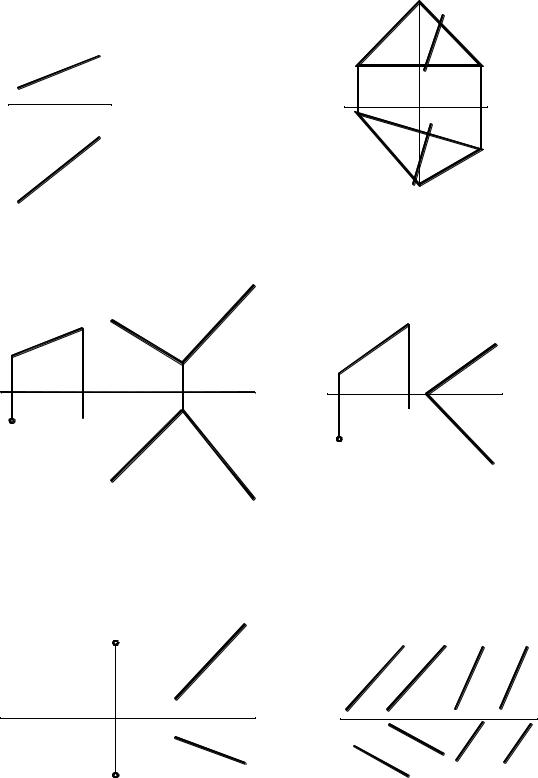
8.18. Достройте горизонтальную проекцию прямой АВ, параллельной плоскости: |
|||||||
а) (а b) ; |
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
б) |
|
|
|
|
|
|
|
|
B2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
A2 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
1 |
8.19. Через точку А проведите плоскость, |
8.20. Проверьте, параллельны ли дан- |
||||||
перпендикулярную плоскости П 2 |
и |
ные плоскости a | | b и m | | n |
|||||
параллельную прямой а. |
|
|
|
|
|
|
|
A2 |
|
|
|
m |
n |
2 |
|
a2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
a2 b2 |
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
b1 |
|
|
|
|
a1 |
a1 |
m |
|
|
|
|
|
n1 |
|
|
||
|
|
|
1 |
|
|
|
A1 |
|
|
|
|
|
|
Тема 8
94
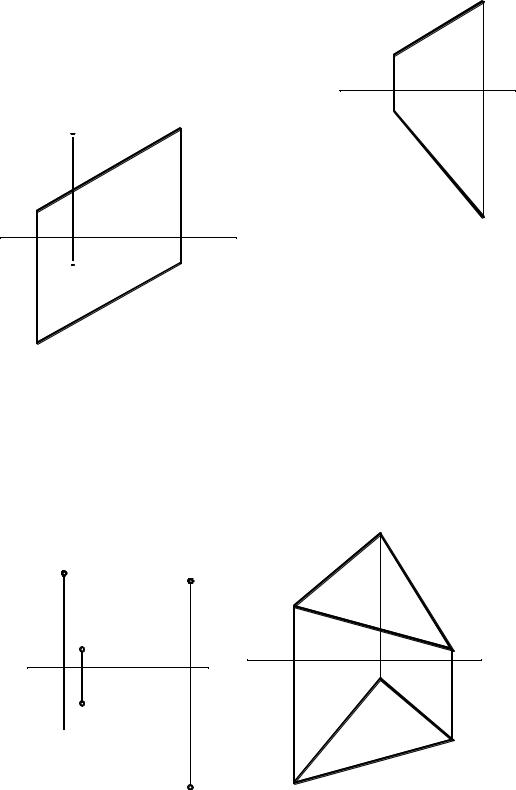
8.21. Определить натуральную величину отрезка АВ и угол наклона его к плоскости проекций П2.
B2
A2
8.22. Определить расстояние от точки А до прямой а. |
x |
A1
A2 


a2
B1
x
A1 


a1
8.23. Построить горизонтальную проекцию |
8.24. Определить угол наклона плоскости |
|
точки А, равноудаленной от точек В и С. |
( АВС) к плоскости проекций П2. |
|
|
|
B2 |
A2 |
C2 |
|
|
|
|
|
|
A2 |
B2 |
|
C2 |
|
|
|
x |
|
x |
|
B1 |
|
|
|
|
B1
C1
C1 A1
Тема 8
95
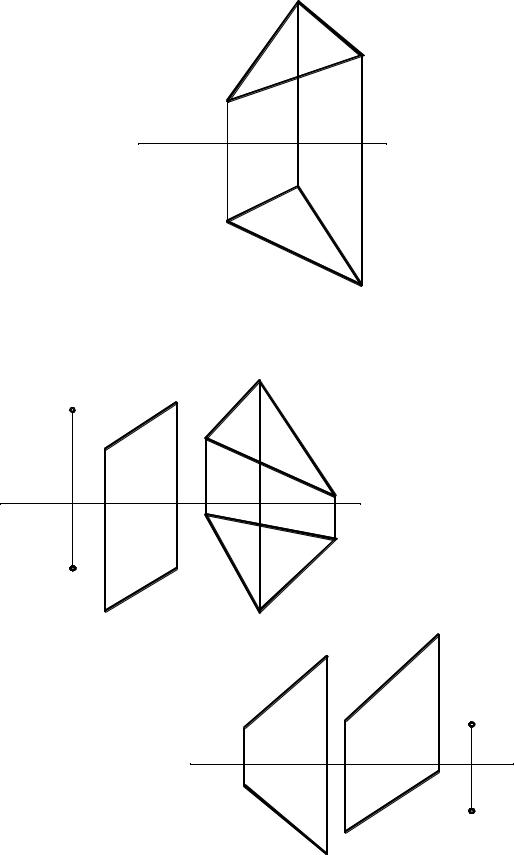
8.25. Построить плоскость Г | | ( АВС) |
B2 |
на расстоянии 20 мм от нее. |
|
C2
A2
xП2 П1
B1
A1
C1
8.26. Через точку А провести прямую, параллельную плоскости ( ВСD) и пересекающую прямую l.
|
|
|
|
C2 |
|
A2 |
|
|
|
|
l2 |
B2 |
|
|
|
|
|
|
|
|
П2 |
|
|
D2 |
x |
|
|
|
|
П |
|
|
|
|
|
1 |
B1 |
|
D1 |
|
|
|
||
|
l1 |
|
|
|
|
A1 |
|
|
|
|
|
|
|
C1 |
|
|
|
|
b2 |
8.27. Построить прямую l, проходящую |
|
|
||
через точку А и пересекающую прямые |
|
|
||
а и b. |
|
|
a2 |
A2 |
|
|
|
|
|
|
x |
П2 |
|
|
|
П |
|
b1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
a1 |
|
|
|
|
|
A1 |
Тема 8
96
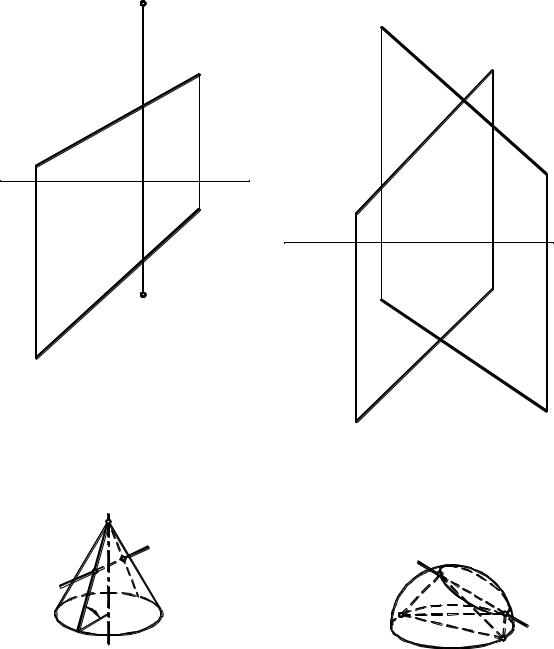
8.28. Через точку А провести прямые, |
8.29. Отрезок АС – гипотенуза |
пересекающие прямую l и наклоненные к |
прямоугольного АВС, вершина прямого |
плоскости проекций П1 под углом 600. |
угла которого находится на прямой l. |
|
Построить проекции треугольника. |
A2 |
|
l |
C2 |
2 |
|
|
П2 |
l2 |
x |
|
|
П |
|
|
|
1 |
|
|
l1 |
A2 |
|
x |
П2 |
|
П |
|
|
|
1 |
|
A1 |
C1 |
|
|
A1 l1
Искомые прямые - образующие конуса вращения, проходящие через точки пересечения прямой l и этого конуса.
Вершины B и B' - точки пересечения прямой l и полусферы, диаметр которой равен | AC |.
Примечание. Задача имеет два решения.
Тема 8
97
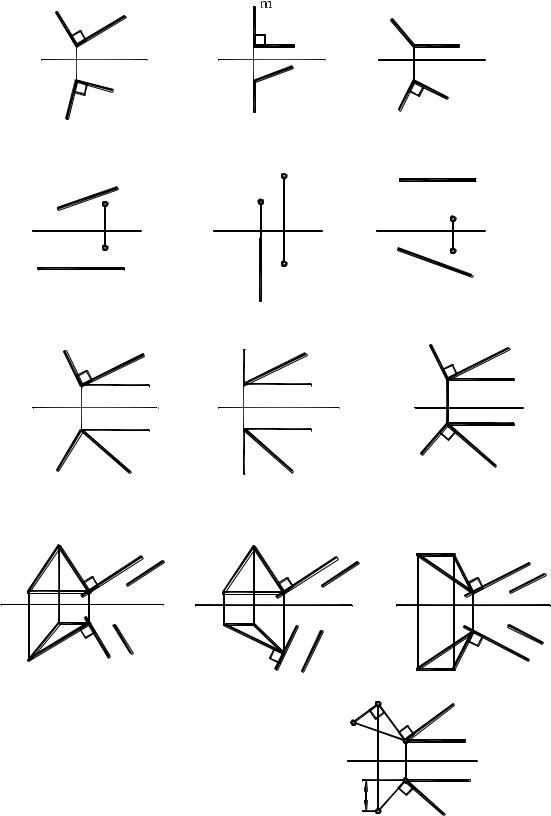
Тест (Тема 8)
8.1. На каком чертеже (а, б, в) заданы взаимно-перпендикулярные прямые?
а) |
|
|
б) |
|
|
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.2. На каком чертеже (а, б, в) расстояние от точки А до прямой изображается в натуральную величину на плоскости П2?
а) |
б) |
в) |
8.3. На каком чертеже (а, б, в) прямая а перпендикулярна плоскости (f h)?
а) |
|
|
|
б) |
|
|
|
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.4. На каком чертеже (а, б, в) заданы взаимно-перпендикулярные плоскости ( АВС) и |
||
Г (a b)? |
|
|
а) |
б) |
в) |
8.5. Какой отрезок (а, б, в, г) определяет величину расстояния от точки А до плоскости
(f h)?
а) |
А2В2 |
б) |
А1В1 |
в) |
А'В2 |
г) |
y |
Тема 8
98
Образовательный модуль 5
Тема 9. Способы преобразования чертежа
Цель: Упрощение решения позиционных и метрических задач.
Задачи: Научиться преобразовывать чертеж введением дополнительной плоскости проекций (заменой плоскости проекций), способом вращения и плоскопараллельным перемещением.
Решение многих позиционных и метрических задач значительно упрощается при частном расположении геометрических образов относительно системы плоскостей проекций. Для перевода г.о. из общего положения в частное сущестует несколько способов преобразования чертежа. Чаще всего применяют способ замены плоскостей проекций, способ вращения и плоскопараллельное перемещение.
9.1. Способ замены плоскостей проекций
|
Дополнительная плоскость проекций вводится перпендикулярно к одной из |
|||
|
основных плоскостей проекций П1 или П2. Выбор основной плоскости проекций, |
|||
|
перпендикулярно которой вводится дополнительная плоскость проекций, производится |
|||
|
в зависимости от условий задачи. Особенностью данного способа преобразования |
|||
|
чертежа является то, что заданный в основной системе плоскостей проекций г.о. не |
|||
|
меняет своего положения и проецируется прямоугольно на новую плоскость проекций. |
|||
|
Дополнительная плоскость вместе с одной из основных плоскостей проекций |
|||
|
|
|
образуют новую систему взаимноперпендикулярных |
|
|
П 2 |
|
плоскостей проекций, для которой справедливы все |
|
|
|
свойства прямоугольного проецирования. |
||
|
|
|
||
|
A2 |
|
|
На рис. 9.1 задана точка А в системе двух плоскостей |
|
|
проекций П1 и П2. Введем дополнительную плоскость |
||
|
|
|
||
|
|
|
проекций П4 и спроецируем на нее точку А (рис. 9.2). |
|
x |
Ax |
A |
|
Алгоритм получения проекции А4 (рис.9.2): |
|
|
|
||
|
|
|
|
|
|
|
A1 |
П 1 |
П1П2 П1П4, П4 П1, x1 = П1 П4, |
|
Рис. 9.1 |
где x1 проводится произвольно, |
||
|
|
|
||
|
|
|
A1AX1 x1 , |AX1A4| = |AXA2| = zA. |
|
|
|
|
|
|
Рис. 9.2
Тема 9
99
