Задания для самостоятельной работы

1. Решить систему линейных уравнений используя правило Крамера и матричный способ

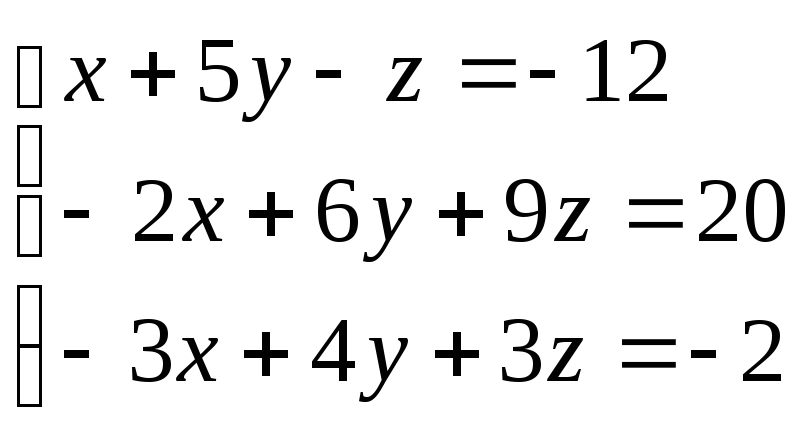
2. Решить систему линейных уравнений используя метод Гаусса:

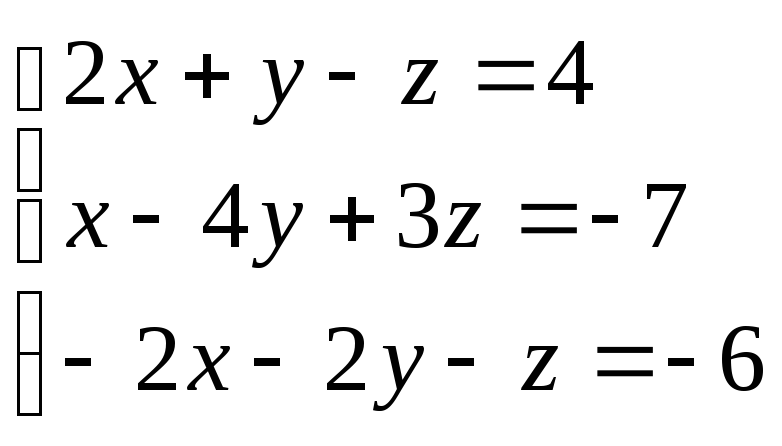
Рекомендуемая литература: 1.1, 2.1.

Самостоятельная работа №3

Тема: «Векторы. Координаты векторов»

Цель: Закрепление умения производить действия над векторами в координатной и геометрической форме. Находить координаты вектора, модуль вектора, скалярное произведение векторов через координаты

Время выполнения: 4 часа

Теоретические сведения

Вектором называется направленный отрезок. Обозначения: a, , .

Векторы называются коллинеарными, если они лежат на одной прямой ли на параллельных прямых.

Вектор называется нулевым, если его начальная и конечная точки совпадают. Нулевой вектор не имеет определенного направления.

Два вектора называются равными, если они коллинеарны, имеют одинаковую длину (модуль) и одинаковое направление.

Проекцией вектора АВ на ось OX (OY) называется длина направленного отрезка А^/В^/ оси OX (OY), где А^/ и В^/ - основания перпендикуляров, опущенных из точек А и В на ось OX (OY).

Проекции вектора на координатные оси – координаты вектора: . Длина вектора находится по формуле

.

Пусть α, β, γ – углы, образованные вектором с осями координат (Ox, Oy, Oz соответственно), тогда

, ,

Линейные операции над векторами.

Суммой a + b векторов a и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а.

Такое правило сложения векторов называют правилом треугольника.

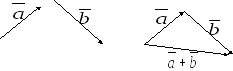
Существует еще одно правило сложения векторов – правило параллелограмма: сумма векторов a и b есть диагональ параллелограмма, построенного на них как на сторонах, выходящая из их общего начала.

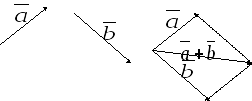
Разностью а – b векторов а и b называется такой вектор с, который в сумме с вектором b дает вектор а.

Произведением ka вектора а на число k называется вектор b, коллинеарный вектору а, имеющий модуль, равный |k||a|, и направление, совпадающее с направлением а при k>0 и противоположное а при k<0.

Если векторы изаданы своими координатами, то их сумма и разность определяются по формулам:

;

Произведение вектора на число определяется формулой

Вектор , имеющий начало в точкеи, определяется через координаты точек А и В:

.

Скалярное произведение векторов

Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними:ab = |a||b| cosφ. Обозначается скалярное произведение: ab, (ab), a·b .

Свойства скалярного произведения:

1. ab = ba .

2. (ka)b = k(ab).

3. (a + b)c = ac + bc .

4. a² = aa = |a|² , где а² называется скалярным квадратом вектора а.

Если векторы а и b определены своими координатами и,то

Отметим условия коллинеарности и перпендикулярности двух не нулевых векторов:

||

┴

Пример 1. Найти длину вектора по заданным координатам его концов,.

Решение:

Находим координаты вектора :, а теперь найдем модуль этого вектора:.

Пример 2. Даны векторы ,и. Определить длину вектора.

Решение:

Найдем координаты вектора . Итак,.

Пример 3. Найти косинус угла между векторами и.

Решение

Из определения скалярного произведения следует, что. По координатам векторов находим:,;, поэтому.

Пример 4.Доказать, что диагонали четырехугольника, заданного координатами вершин А(-4;-4;4), В(-;2;2), С(2;5;1), D(3;-2;2), взаимно перпендикулярны.

Решение:

Составим вектора лежащие на диагоналях данного четырёхугольника. Имеем:

Проверим, ортогональны ли эти вектора. Для этого найдём их скалярное произведение:

Отсюда следует, что вектора, лежащие на диагоналях четырёхугольника ортогональны, а значит, диагонали взаимно перпендикулярны и данный четырёхугольник является параллелограммом