Общие требования к оформлению и выполнению самостоятельной работы

Форма отчетности:

1. самостоятельные работы требуется выполнять в отдельной тетради для самостоятельных работ;

2. каждая работа должна содержать:

• номер и название самостоятельной работы;

• цель работы;

• условия заданий;

• подробное решение заданий.

Самостоятельная работа №1

Тема: «Вычисление определителей матрицы»

Цель: Закрепление умения вычислять, миноры, алгебраические дополнения и определители четвертого порядка разложением по элементам строки (столбца).

Время выполнения: 2 часа

Теоретические сведения

Квадратной матрице А порядка n можно сопоставить число det A (или , или), называемое еёопределителем, следующим образом:

1. если , тои;

2. если , тои;

3. если , тои

Определитель матрицы А также называют её детерминантом.

Вычисление определителя 2-го порядка иллюстрируется схемой:

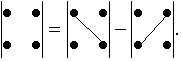
Пример 1. Найти определители матриц: и.

Решение:

При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое схематически можно записать так:

Пример 2. Вычислить определитель матрицы

Решение:

Для вычисления определителей более высоких порядков используются понятия минора и алгебраического дополнения.

Минором некоторого элемента определителя n-го порядка называется определитель (n – 1)-го порядка, полученный из данного путём вычёркивания строки и столбца, на пересечении которых находится выбранный элемент. Минор каждого элемента обозначается символом. Так, если, то,.

Алгебраическим дополнением элемента определителя называется его минор, умноженный на, т.е.

Так,

Определитель матрицы равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.

Например,

Данное свойство содержит в себе способ вычисления определителей высоких порядков.

Пример 3. Вычислите определитель .

Решение:

Задание для самостоятельной работы

Вычислить определители:

Рекомендуемая литература: 1.1, 2.1.

Самостоятельная работа №2

Тема: «Решение систем линейных уравнений»

Цель: Закрепление навыков решения систем линейных уравнений по правилу Крамера, матричным методом и методом Гаусса.

Время выполнения: 4 часа.

Теоретические сведения

Пусть дана система из n линейных уравнений с n неизвестными

(1)

Числа называютсякоэффициентами системы (1), а числа -свободными членами.

Система линейных уравнений называется однородной, если .

Матрица называетсяматрицей системы (1), а её определитель -определителем системы (1).

Решением системы (1) называется совокупность чисел, , которые обращают все уравнения системы в тождества.

Система, у которой число неизвестных равно числу уравнений, называется совместной. В противном случае система называется несовместной.

Правило Крамера. (Крамер Г. (1704-1752) – швейцарский математик)

Решение системы (1) n линейных уравнений с n неизвестными удобно записывать и вычислять с помощью определителей.

Главным определителем системы называется определитель матрицы А, составленный из коэффициентов при неизвестных, т.е., .

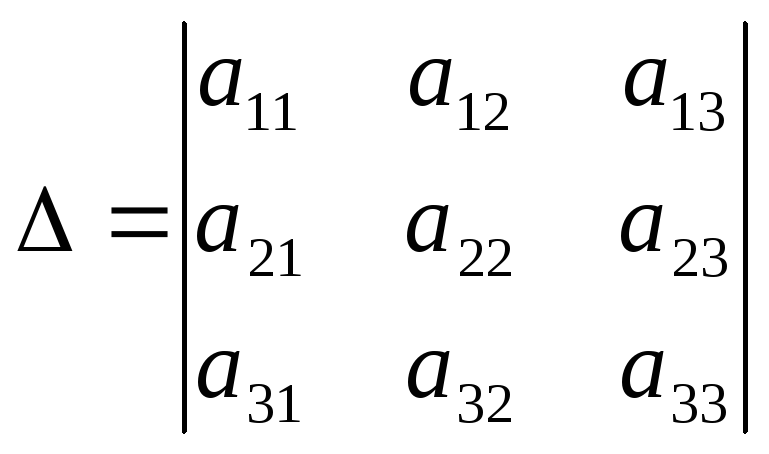Определитель получится из главного определителя заменой в нём первого столбца столбцом свободных членов, определитель- заменой второго столбцом свободных членов и т.д.

Неизвестные находятся из соотношений:.

Пример 1. Решить систему уравнений методом Крамера.

Решение:

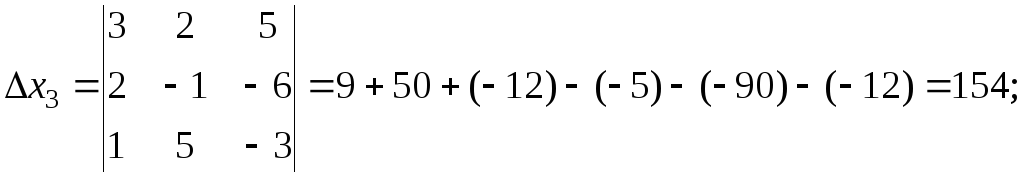
Проверка:

Ответ:

Матричный способ решения систем линейных уравнений

Систему (1) запишем в матричной форме , где

, и.

Если ,то матрица А имеет обратную и система (1) имеет единственное решение, которое находится по формуле.

Решение систем линейных уравнений методом Гаусса

Элементарные преобразования матриц

 Перестановка местами двух параллельных рядов матрицы;

 Умножение всех элементов ряда матрицы на число, отличное от нуля;

 Прибавление к элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается .

Расширенной матрицей назовём следующую матрицу:

С помощью элементарных преобразований матрицу по методу Гаусса можно привести к виду:

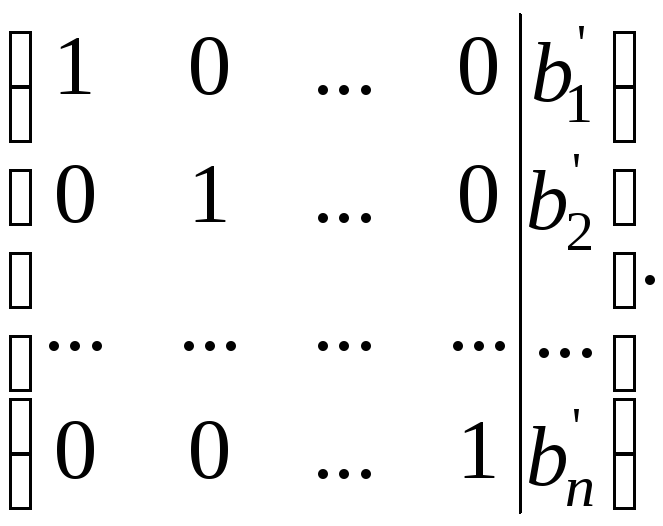
Тогда

Для формализации преобразования матрицы введёмправило прямоугольника.

Рассмотрим прямоугольник из 4-ёх элементов матрицы :

Назовём элемент ведущим, строку, в которой он стоит -ведущей строкой. По правилу прямоугольника пересчитывается элемент, стоящий по диагонали от ведущего элемента по следующей формуле:

Очевидно, что формула упростится, если ведущий элемент . Поэтому, если в системе есть элементы равные 1, то их рекомендуется выбирать ведущими.

Для проверки верности счёта к расширенной матрице приписывается столбец сумм, элементы которого равны построчным суммам матрицы . Над элементами контрольного столбца производятся те же операции, что и над элементами матрицы. Если сумма строки равна соответствующему элементу контрольного столбца, рассчитанного по правилу прямоугольника, то счёт ведётся верно, в противном случае следует искать ошибку в счёте.

Пример 3. Решить систему уравнений:

Решение:

Выпишем матрицу ; припишем к ней контрольный столбец.

За ведущий элемент примем 1, стоящую в первой строке и 3–ем столбце (Ведущими можно выбирать только элементы основной матрицы, т.е. матрицы без столбца свободных членов). Ведущую строку перепишем без изменения, в ведущем столбце запишем нули, все остальные элементы пересчитаем по правилу прямоугольника:

т.е.

Пример пересчёта элемента 2, стоящего во второй строке и первом столбце:

Пример пересчёта элемента -1, стоящего во второй строке и втором столбце:

Далее примем за ведущий элемент единицу, стоящую в третьей строке и первом столбце. Третью строку и третий столбец перепишем без изменения, в первом столбце запишем нули, остальные элементы пересчитаем по правилу прямоугольника:

т.е.

Разделим вторую строку на 2 (это равносильно делению обеих частей уравнения на 2), получим

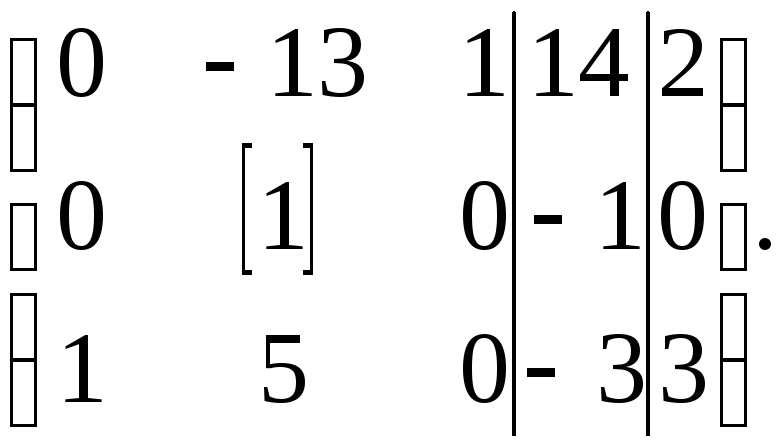
Выбираем ведущей 1, стоящую во второй строке и втором столбце (заметим, что строка и столбец могут быть ведущими только 1 раз).

Вторую строку, первый и третий столбцы переписываем без изменения, во втором столбце записываем нули, остальные элементы пересчитываем по правилу прямоугольника.

т.е.

Таким образом получили ответ