4. Задача про максимальний потік у транспортній мережі

Транспортною мережею (s/t-мережі) назвемо зв`язний орієнтований граф без петель, у якого є дві особливі вершини s (джерело) та t (стік). Причому:

з вершини s дуги тільки виходять, а у вершину t – тільки заходять;

кожній дузі транспортної мережі приписана невід`ємна величина, яка називається пропускною спроможністю дуги і позначається c_ij.

Зафіксуємо деяку вершину s/t-мережі х_к. Для поняття потоку транспортної мережі розглянемо дві множини А-множина всіх вершин s/t-мережі, з яких виходить дуга та заходить у вершину х_к, та В – множина всіх вершин s/t-мережі, які безпосередньо слідують за вершиною х_к. Тоді потоком в s/t-мережі будемо називати невід`ємну величину j_ij (для деякої дуги u_ij)=v, якщо виконуються наступні умови:

j_ij £ c_ij , для будь-якої дуги графа;

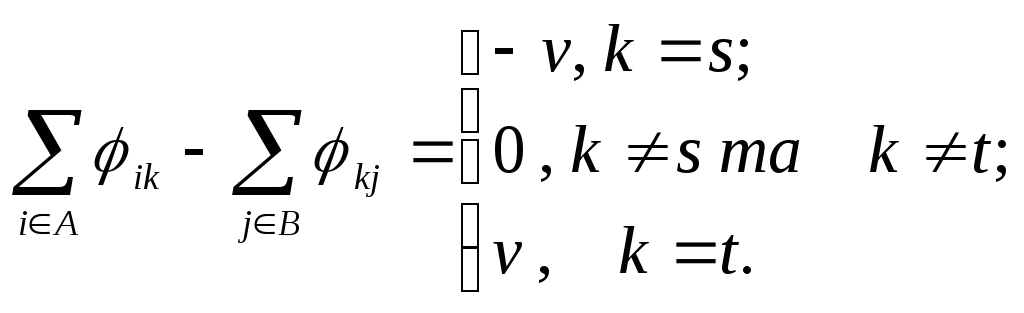
Перша умова говорить, що для будь-якої дуги транспортної мережі потік не перевищує пропускну спроможність транспортної мережі, а друга про те, що для будь –якої вершини транспортної мережі сумарний потік, що входить у вершину, рівний сумарному потоку, що виходить з вершини, тобто потік неподільний.

Нехай Х – множина всіх вершин s/t-мережі. Розіб`ємо її на дві підмножини Х₁ та Х₂ таким чином, щоб:

Тоді розтином s/t-мережі назвемо множину всіх дуг, що слідують з множини вершин Х₁ до множини вершин Х₂, позначимо (Х₁, Х₂). Величина розтину рівна сумі пропускних спроможностей дуг, що створюють розтин, та позначається v(X₁, X₂).

Задача про визначення максимального потоку в транспортній мережі є основною задачею оптимізації на графах. Її рішення базується на наступній теоремі Форда-Фалкерсона: максимальний потік у транспортній мережі дорівнює величині найменшого розтину в ній.

Задача 4. Транспортну мережу задано графічно. Необхідно знайти максимальний потік в s/t-мережі.

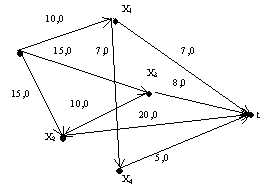
Розв`язок. Кожній дузі графа припишемо пару чисел c<sub>ij</sub>, j<sub>ij</sub>. На початку в s/t-мережі розподілимо нульовий потік, тобто j<sub>ij</sub>=0. Далі для розмітки будь-якої к-ї вершини будемо використовувати позначення к(і<sup>+</sup>, e(к)) або к(і<sup>-</sup>, e(к)), де і- номер вершини, з якої ми потрапили до вершини к, ‘+’ - по прямій дузі, ‘-‘ - по зворотній дузі, e(к) – невід`ємна величина, на яку можна збільшити потік (для прямої дуги) або зменшити (для зворотної дуги). Вершина s завжди має особливу помітку (s⁺, ¥). Помічати вершини по прямих дугах можна, якщо на цих дугах потік можливо збільшити ( c_ij-j_ij >0), а по зворотніх – якщо потік можливо зменшити (j_ij >0). Для вершини к(і⁺, e(к)) e(к)=min(e(i), c_ik-j_ik), а для вершини к(і^-, e(к)) e(к)=min(e(i), j_ik). Перший крок будь-якого етапу полягає у розставленні поміток вершин мережі, доки або не буде помічено вершину t , тоді переходимо на другий крок, або переконаємося, що вершину t помітити неможливо (задачу вирішено).

1-й єтап.

1-й крок. S(s⁺,¥). Далі помічаємо вершини суміжні з s. 1(s⁺, min(¥,10-0) , тобто 1(s⁺,10). Аналогічно 2(s⁺,15), 3(s⁺,15). Тепер вершина s розглянута. Для подальшого розгляду вибираємо будь-яку із суміжних помічених вершин. Наприклад, вершину 3. Помічаємо вершини, суміжні з третьою: 2(3⁺, min(15, 10-0)=10), t(3⁺, min(15,8-0)=8) Помітили вершину t – переходимо до друго кроку 1-го етапу.

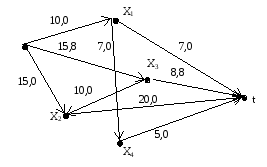
2-й крок. За допомогою поміток вершин будуємо ланцюг, який приводить з вершини s у вершину t: t¬3¬s. На прямих дугах ланцюга потік збільшуємо на величину e(t), а на зворотній – зменшуємо на цю саму величину. На малюнку показано розподіл потоку після виконання першого етапу. Переходимо до другого етапу, який виконуємо аналогічно першому.

2-й етап.

S(s+,¥)

1(s+,10) 2(s+,15) 3(s+,7)

t(2+,15) t¬2¬s e(t)=15

3-й етап.

S(s+,¥)

1(s+,10) 3(s+,7)

4(1+,7) t(1+,7) t¬1¬s e(t)=7

Після 2-го та 3-го етапів розподіл потоку у мережі показано на малюнку.

4-й етап.

S(s+,¥)

1(s+,3) 3(s+,7)

2(3+,7)

t(2+,5) t¬2¬3¬s e(t)=5

5-й етап.

S(s+,¥)

1(s+,3) 3(s+,2)

4(1+,3)

t(4+,3) t¬4¬1¬s e(t)=3

6-й етап.

S(s+,¥)

3(s+,2)

2(3+,2)

S(2-,2)

На 1-му кроці 6-го етапу прийшли до побудови контуру навколо вершини s, а в вершину t так і не потрапили. Це свідчить про те, що потік у мережі збільшити неможливо. Будуємо розтин мережі: віднесемо до множини Х₁ усі вершини, що помічені на 6-му кроці, а до множини Х₂ – ті, що не помічені. Х₁={s, 2, 3}, X₂={1, 4, t}, (X₁, X₂)={u_s1, u_2t, u_3t}, v(X₁, X₂)=c_s1+c_2t+c_3t=10+20+8=38. Перевірка: якщо просумувати всі значення e(t): 8+15+7+5+3=38, то отримаємо те саме значення величини розрізу.

Результуючій розподіл потоку в мережі має вигляд

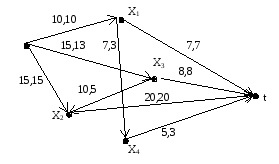
На малюнку також показано розріз найменшої величини, який побудовано у розглянутому прикладі.