Вопрос 72. Понятие о нормальном распределении случайных величин (распределении Гаусса), основания к применению нормального распределения, параметрическая и непараметрическая статистика.

Нормальное распределение (распределение Гауса)- это распределение вероятностей, которое в одновременном случае задается функцией плотности вероятности, совпадающей с функцией Гауса :

Основания к применению нормального распределения :

• многие реально наблюдаемые переменные действительно нормально распределены, что является аргументом в пользу того, что нормальное распределение представляет "фундаментальный закон"

• при возрастании объема выборки форма выборочного распределения приближается к нормальной, даже если распределение исследуемых переменных не является нормальным

Статистические методы, основанные на предположении о нормальном распределении исследуемых выборок, называются параметрическими.

Непараметрическая статистика это-статистические технические приемы, которые не допускают особенных функциональных форм для отношений между переменными.

Основное преимущество непараметрических критериев по сравнению с параметрическими состоит в том, что они могут быть использованы при любых распределениях выборок, отличающихся от нормального закона.

73)Численные оценки параметров распределения случайной величины, характеризующих центр распределения. Средние значения, их расчет, свойства, способы применения в медицинской статистике.

Параметры распределения случайной величины

Для характеристики центра распределения используются следующие параметры:

• Мода

• Медиана

• Среднее арифметическое значение

Мода - наиболее часто встречающаяся варианта в простом вариационном ряду.

Медиана - варианта, занимающая в простом вариационном ряду серединное положение.

Среднее арифметическое значение- одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех зафиксированных значений, делённую на их количество.

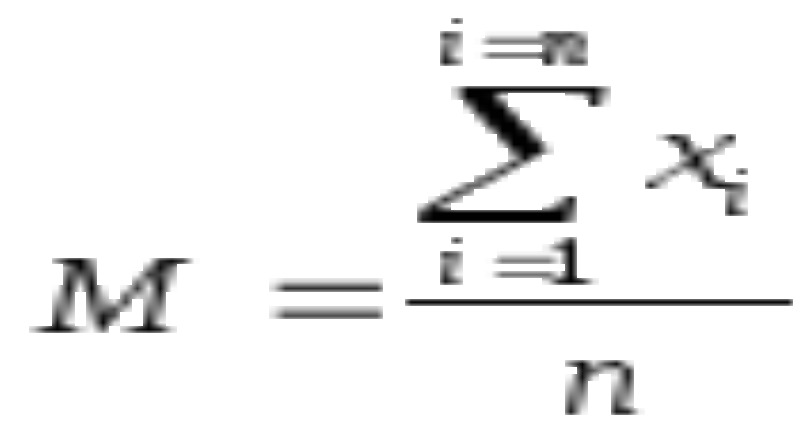
Основное значение средних величин состоит в их обобщающей функции, и на практике они применяются для обобщения значений.

75. Численные оценки параметров, характеризующих отклонение изучаемых распределений от нормального распределения (распределения Гаусса).

При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. С этой целью вводят специальные характеристики, в частности асимметрию и эксцесс. Для нормального распределения эти характеристики равны нулю. Поэтому если для изучаемого распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость этого распределения к нормальному. Наоборот, большие значения асимметрии и эксцесса указывают на значительное отклонение от нормального. Как оценить асимметрию? Можно доказать, что для симметричного распределения (график такого распределения симметричен относительно прямой χ = Μ (Χ)) каждый центральный момент нечетного порядка равен нулю. Для несимметричных распределений центральные моменты не четного порядка отличны от нуля. Поэтому любой из этих моментов (кроме момента первого порядка, который равен нулю для любого распределения) может служить для оценки асимметрии; естественно выбрать простейший из его величина зависит от единиц, в которых измеряется случайная величина. Чтобы устранить этот недостаток, характеристику.

77)Стандартные ошибки для средних значений, относительных показателей. Интервальные оценки параметров распределений. Доверительная вероятность. Доверительный интервал. Расчет доверительных интервалов для средних значений.

1. Средние величины в статистическом понимании – это обобщающие показатели совокупности однотипных явлений по какому-либо количественному признаку.

Относительный показатель в статистике – это обобщающая величина, которая дает числовую меру соотношения двух сопоставляемых числовых мер абсолютных показателей. Так как многие абсолютные величины взаимосвязаны, то и относительные величины одного типа в ряде случаев могут определяться через относительные величины другого типа. Основное условие правильного расчета относительной величины – сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями. Таким образом, по способу получения относительные показатели – всегда величины производные, представляющие собой частное от деления двух абсолютных величин и характеризующие количественное соотношение между ними.

Одним из условий правильного использования статистических показателей является изучение абсолютных и относительных величин в их единстве. Если это условие не соблюдено, можно прийти к неправильному выводу. Только комплексное изучение абсолютных и относительных величин дает всестороннюю характеристику изучаемого явления.

При оценке вероятностных характеристик по ограниченному числу опытов могут быть допущены ошибки, т. е. отклонения этой оценки от истинного значения характеристики случайной величины.

Чтобы убедиться в том, что мы не допускаем чрезмерно грубой ошибки в оценке какой-то вероятностной характеристики, в теории вероятностей и математической статистике пользуются так называемыми доверительными интервалами и доверительными вероятностями.

2. Интервальной называют оценку, которая определяется двумя числами – концами интервала.

Допустим, что для изучения некоторой случайной величины X (признака генеральной совокупности) необходимо по статистическим данным произвести оценку неизвестного ее параметра θ (это может быть М(Х), D(Х) или р) с определенной степенью точности и надежности, т. е. надо указать границы, в которых практически достоверно лежит этот неизвестный параметр θ.

3. Доверительная вероятность — вероятность того, что доверительный интервал накроет неизвестное истинное значение параметра, оцениваемого по выборочным данным

4. Доверительный интервал – интервал, который покрывает неизвестный параметр с заданной надёжностью.

5. Доверительные интервалы для среднего задают область вокруг среднего, в которой с заданным уровнем доверия содержится "истинное" среднее. В Основных статистиках вы можете построить доверительные интервалы для любого p-уровня; например, если среднее в вашей выборке равно 23, а нижняя и верхняя границы для p=.05 равны 19 и 27 соответственно, то вы можете заключить, что с 95% вероятностью среднее выборки больше 19 и меньше 27.

Билет №79. Параметрические критерии для сравнения выборочных средний значений и дисперсий. (критерий Стьюдента, критерий Фишера)

Если вид распределения или функция распределения выборки нам заданы, то в этом случае задача оценки различий двух групп независимых наблюдений может решаться с использованием параметрических критериев статистики: либо кри­терия Стьюдента (t), если сравнение выборок ведется по сред­ним значениям (X и У), либо с использованием критерия Фишера (F), если сравнение выборок ведется по их дисперсиям.

Критерий Стьюдента (t-критерий)

Критерий позволяет найти вероятность того, что оба средних значения в выборке относятся к одной и той же совокупности. Данный критерий наиболее часто используется для проверки гипотезы: «Средние двух выборок относятся к одной и той же совокупности».

При использовании критерия можно выделить два случая. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух неза­висимых, несвязанныхвыборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и экспериментальная (опытная) группа, количество испытуемых в группах может быть различно.

Во втором случае, когда одна и та же группа объектов порождает числовой матери­ал для проверки гипотез о средних, используется так называемый парный t-критерий. Выборки при этом называют зависимыми, связанными.

F — критерий Фишера

Критерий Фишера позволяет сравнивать величины выбороч­ных дисперсий двух независимых выборок. Для вычисления F_эмп нуж­но найти отношение дисперсий двух выборок, причем так, что­бы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Формула вычисления критерия Фи­шера такова:

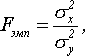                                                                                                  (8)

где - дисперсии первой и второй выборки соответственно.

Так как, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значе­ние F_эмп всегда будет больше или равно единице.

Чис­ло степеней свободы определяется также просто:

k₁=n_l - 1 для первой выборки (т.е. для той выборки, величина дисперсии которой больше) и k₂=n₂ - 1 для второй выборки.

В Приложе­нии 1 критические значения критерия Фишера находятся по величинам k₁ (верхняя строчка таблицы) и k₂ (левый столбец таблицы).

Если t_эмп>t_крит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.

Вопрос №81

Способы анализа взаимосвязей различных явлений. Статистическая и функциональная связь. Численные оценки силы и направления корреляционной связи

Анализ взаимосвязей, присущих изучаемым процессам и явлениям, является важнейшей задачей исторических, как впрочем и многих других, исследований. В тех случаях, когда речь идет о явлениях и процессах, обладающих сложной структурой и многообразием свойственных им связей, такой анализ представляет собой сложную задачу. Прежде всего необходимо установить наличие взаимосвязей и их характер. Вслед за этим возникает вопрос о тесноте взаимосвязей и степени воздействия различных факторов (причин) на интересующий исследователя результат. Если черты и свойства изучаемых объектов могут быть измерены и выражены количественно, то анализ взаимосвязей может вестись на основе применения математических методов. Использование этих методов позволяет проверить гипотезу о наличии или отсутствии взаимосвязей между теми или иными признаками, выдвигаемую на основе содержательного анализа. Далее, лишь посредством математических методов можно установить тесноту и характер взаимосвязей или выявить силу (степень) воздействия различных факторов на результат.