Примеры решения задач

Задача 1.Уравнение движения материальной точки по прямой имеет вид x = 4 + 2 t + + 0,2 . Найти:

1) положение точки в момент времени = 2 с, = 5 с;

2. среднюю скорость за время, протекшее между этими моментами;

3. мгновенные скорости в указанные моменты времени;

4. среднее ускорение за указанный промежуток времени;

5. мгновенные ускорения в указанные моменты времени.

Дано:

x = 4 + 2 t + + 0,2 м

= 2 с

= 5 с

-? -? V_ -? V₂ -? V -?

 a -? -? -?

Решение

1) Положение точки определяется значением координаты x в указанные моменты времени. Подставим заданные момент времени t₁ и t₂ в уравнение движения:

= (4 + 2^.2 + 4 + 0,2 ^. 8)м = 13,6 м; x₂ = (4 + 2^.5 + 5² + 0,2 ^. 5³)м = 64 м.

2) Значение средней скорости , гдеx - изменение расстояния за промежуток времени t.

3. Общее выражение мгновенной скорости имеет вид

.

Подставив в это выражение заданные значения времени, получим

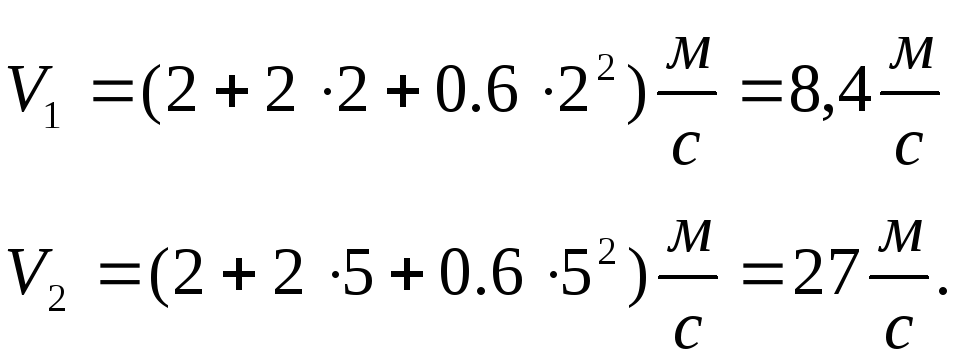
4. Среднее ускорение , где V - изменение скорости за промежуток времени t.

5. Общее выражение мгновенного ускорения имеет вид

Подставив численное значение и , получим

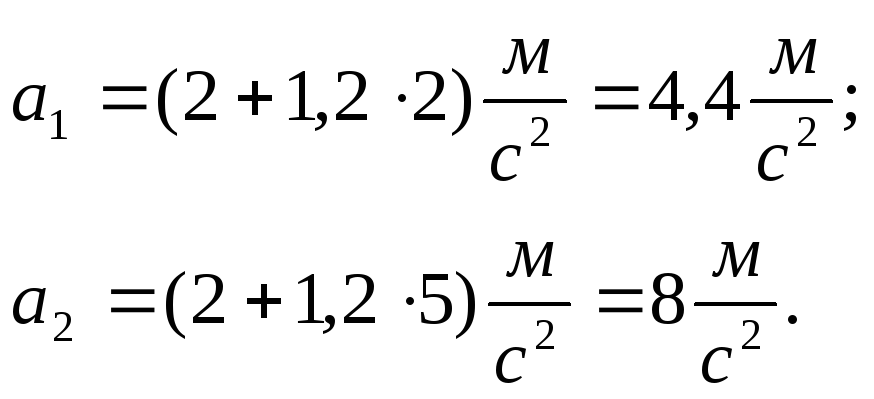
Ответ:

Задача 2. Начертить график зависимости координаты и пути от времени движения, заданного уравнением x = 5 + 4 t  .

Решение Для построения графика найдем характерные значения координаты: начальную координату, максимальную координату и равную нулю, моменты времени, соответствующие им.

1) Начальная координата соответствует t = 0, = x= 5.

2) Максимального значения координата достигает в тот момент, когда скорость меняет знак (точки начинают двигаться в обратном направлении). Этот момент времени найдем, взяв первую производную от координаты по времени и приравняв ее нулю:

, откуда t = 2 c.

Максимальная координата равна .

3) Найдем момент времени, когда координата равна нулю:

.

Решая это квадратное уравнение, получим два корня:

= 5 c, = 1 c.

Второй корень физического смысла не имеет. Для построения графика зависимости координаты от времени имеем:

t = 0; = 5 м; V₀ = 4 м/с;

t = 2 c; x_max = 9 м; V₀ = 0;

t = 5 c; x = 0.

График зависимости пути от времени строим, исходя из того, что:

1) путь и координата совпадают, пока скорость не изменит знак;

2) начиная с момента изменения знака скорости, координата убывает, а путь возрастает по тому же закону, по которому убывает координата (рис.1.2).

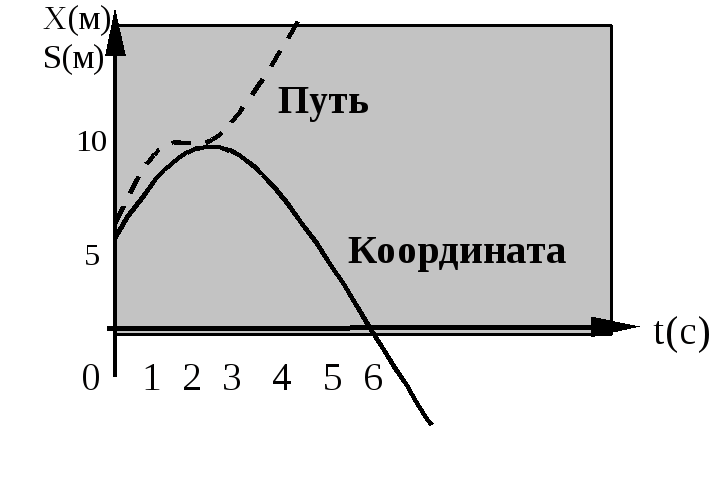
Рис.1.2

Задача 3. Поезд движется с начальной скоростью V₀ =180 км/ч. Внезапно на пути возникает препятствие, и машинист включает тормозной механизм. С этого момента скорость изменяется по закону V = V₀ – α t². Каков тормозной путь поезда? Через какое время после начала торможения он остановится?

Дано:

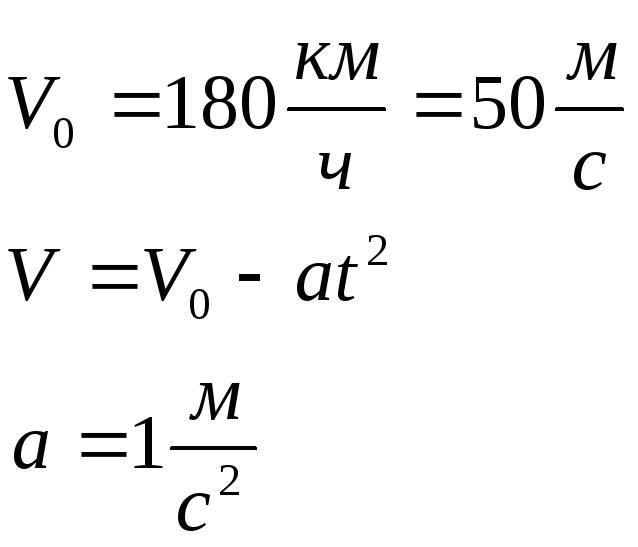
S - ?, t - ?

Решение

Поезд в условиях задачи можно принять за материальную точку. Движение поезда исследуется формально, без выяснения причин, обуславливающих изменение движения. Известен закон изменения одного из параметров движения – скорости. Нужно определить другие величины, характеризующие движение поезда.

Стоящая задача формулируется следующим образом: скорость материальной точки изменяется по закону V = V₀ – α . Определить время движения и путь, который она пройдет до остановки, если при t = 0, x = 0, V = V₀.

Для нахождения закона движения данной материальной точки имеем одно уравнение

Интегрируем уравнение с учетом начальных условий:

Время движения поезда определяется из условия, что скорость его равна 0 (остановка) отсюда

Подставив числовые значения, получаем

Тормозной путь

Ответ: t = 7 c, S = 230 м.

Задача 4. Камень брошен вертикально вверх над колодцем глубиной h = 10 м с начальной скоростью V₀ = 14 м/с. Через сколько времени камень достигнет дна колодца?

Дано:

h = 10 м

V₀ = 14 м/с

t_к - ?