2.5. Зоны Бриллюэна

Условие трансляционной симметрии волновой функции не нарушится, если волновой векторзаменить на вектор, где- вектор трансляции обратной решетки.

Действительно, согласно (2.14)

, (2.40)

так как скалярное произведение векторов прямой и обратной решеток , т.е. для целыхm и всех векторов решетки Бравэ.

Полученный результат означает, что к любому вектору , характеризующему состояние электрона в среде с периодическим потенциалом, всегда можно добавить любой векторобратной решетки, причем это изменение не приводит к изменению состояния электрона. Следовательно, энергия электронов, находящихся в этих двух состояниях, одинакова. Другими словами, энергия электрона в кристалле является периодической функцией волнового вектора с периодом(или)

. (2.41)

Если в -пространстве построить обратную решетку, то все-пространство можно разделить на области, в которых имеются физически эквивалентные состояния. Такие области называютсязонами Бриллюэна. Тогда изменение волновой функции и энергии электрона можно рассматривать не во всем -пространстве, а лишь в пределахпервой зоны Бриллюэна, объем которой ограничен пределами изменения волнового вектора

. (2.42)

Поскольку вектора определены с точностью до, возникает вопрос о выборе начального вектора. Обычно за такой вектор принимают тот из них, который ближе других расположен к началу координат-пространства. Для простой кубической решетки области, в которых будут находиться все такие вектора, будут иметь границы

, ,. (2.43)

Здесь , (или,) где индекс 1 указывает на то, что за,,принимают их наименьшие значения.

Так как вектора нахо­дятся с точностью до, то лю­бая функция может быть переве­дена в первую зону Бриллюэна. Для э

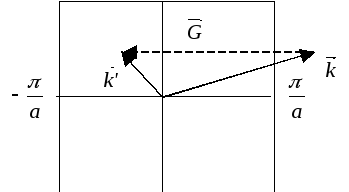
Рис. 2.7. Схема приведения волнового вектора к первой зоне Бриллюэна.

того из рассматриваемого вектораследует вычесть век­тор, чтобы их разность-оказалась внутри или на границе первой зоны Бриллюэна (рис. 2.7). Процедура приведения произ­вольного векторак первой зоне Бриллюэна получила названиесхемы приведенных зон (рис. 2.8).

С

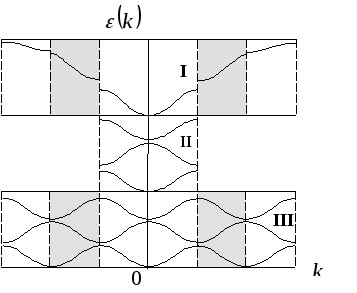
Рис. 2.8 Изображениедисперсионной зависимости в схемах расширенной (I) приведенной (II) и повторяющей (III) зон.

хема изображения зон в-пространстве без приведения к первой зоне называетсясхемой расширенных зон. Иногда оказывается удобным транслировать результат приведения во все зоны Бриллюэна. Такая схема получила название схемы повторяющихся зон.

Изменению энергии , отвечающей изменению внутри одной зоны Бриллюэна, соответствует энергетическая зона. В схеме приведенных зон одной энергетической зоне соответствует изменение функции при одноразовом проходе внутри зоны Бриллюэна. В этом случае для различия разных энергетических зон их часто нумеруют дополнительным индексом. Состояние электрона с волновым вектором в энергетической зоне с индексом будет описывать функция .

Еще раз обратим внимание читателя: зона Бриллюэна – зона в -пространстве, а энергетическая зона - зона в шкале энергий.