Глава 2

Зонная теория твердых тел

2.1. Уравнение Шредингера для твердого тела

Квантовая теория свободных электронов довольно успешно объясняет многие свойства металлов. Трудности возникают при рассмотрении вопроса о том, почему одни химические элементы в кристаллическом состоянии оказывается металлами, другие – изоляторами или полупроводниками, электрические свойства которых резко зависят от температуры. Чтобы уяснить различие между диэлектриками и полупроводниками, модель свободных электронов необходимо дополнить учетом того обстоятельства, что твердые тела обладают периодической атомной структурой.

Для количественного рассмотрения свойств твердого тела исходным пунктом является уравнение Шредингера

, (2.1)

где волновая функция кристалла зависит от координат всех частиц в кристалле, электронови ядер:, а гамильтониандолжен учитывать все виды энергии: кинетическую и потенциальную энергию всех электронов и ядер, энергию взаимодействия электронов и ядер, а также потенциальную энергию всех частиц во внешнем поле.

Поскольку уравнение (2.1) в общем виде решить невозможно из-за огромного числа частиц, для его решения прибегают к различным упрощающим предположениям. Одним из методов, позволяющих упростить уравнение Шредингера, является адиабатическое приближение или приближение Борна-Оппенгеймера.

Сущность этого метода заключается в следующем. При образовании кристалла из отдельных атомов химические связи осуществляются только валентными электронами, тогда как большая часть электронов прочно связана в оболочках (электроны остова) и не влияет на свойства твердого тела. Поэтому ионы решетки и валентные электроны можно рассматривать как независимые элементы. Так как масса ядра намного больше массы электрона, характер движения этих частиц существенно отличен. Можно считать, что ядра остаются в покое по отношению к мгновенному положению электронов. а значит, движение электронов и ядер происходит без обмена между ними энергий. Таким образом, адиабатическое приближение исходит из предположения о независимом характере движения электронов и ядер.

Если воспользоваться наиболее грубым приближением, полагая, что ядра фиксированы, то уравнение Шредингера для отыскания стационарных состояний валентных электронов запишется в виде

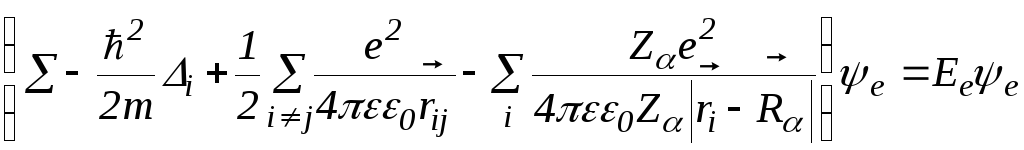, (2.2)

где - волновая функция системы, найденная в предположении покоящихся ядер,Е_e - энергия всей электронной системы, - заряд ядра,и- диэлектрические постоянные вакуума и кристалла.

В выражение (2.2) входит не только энергия взаимодействия каждого электрона в поле всех ионов решетки, но и энергия кулоновского взаимодействия электронов друг с другом. Для случая покоящихся ядер кинетическая энергия ядер обращается в нуль, а энергия их взаимодействия принимает постоянное значение. Следовательно, потенциальную энергию взаимодействия электронов с ядрами можно представить как потенциальную энергию i-го электрона в поле всех ядер

. (2.3)

Столь сложное уравнение, как (3.2), не может быть решено в общем виде. Трудность решения этой задачи заключается во взаимодействии электронов друг с другом. Если бы не было этого взаимодействия, то многочастичная задача свелась бы к одночастичным задачам. Последние описывают не возмущенное движение одного электрона в усредненном поле всех остальных электронов. Такое одноэлектронное приближение известно как приближение Хартри-Фока.

В методе Хартри-Фока усредненное поле является самосогласованным, поскольку не только определяет движение данного электрона, но и само зависит от его движения.

Предполагая, что такое поле найдено, перепишем уравнение (2.2) в виде

. (2.4)

- потенциальная энергия i-го электрона в эффективном поле остальных электронов.

Это уравнение можно записать как

, (2.5)

где - гамильтонианi-го электрона. В соответствии с (2.5) полная энергия представляет собой сумму операторов полной энергии для всех электронов, т.е..

Поскольку теперь гамильтониан не содержит энергии взаимодействия электронов и представляет собой сумму гамильтонианов отдельных электронов, волновая функция системы частиц может быть представлена как произведение одноэлектронных функций (как для невзаимодействующих частиц)

. (2.6)

Каждая функция удовлетворяет одноэлектронному уравнению Шредингера

, (2.7)

где ,,- соответственно гамильтониан, волновая функция и энергия электрона в кристалле.

Если ввести обозначение для потенциальной энергии электрона в кристалле через функцию , то уравнение Шредингера (2.7) примет вид

. (2.8)

Так как в кристалле атомы расположены строго периодически, полный потенциал должен обладать трехмерной периодичностью. Точный вид потенциаланеизвестен, хотя для некоторых диэлектриков и металлов может быть вычислен. Однако для получения многих фундаментальных результатов важно знать, что потенциалявляется периодической функцией с периодом кристаллической решетки.

И

Рис. 2.1. Схематическое изображение периодического потенциала одномерной решетки.

сходя из качественных соображений, можно примерно представить вид типичного периодического потенциала: вблизи иона он должен напоминать потенциал отдельного атома и выравниваться в области между ионами (см. рис.3.1).

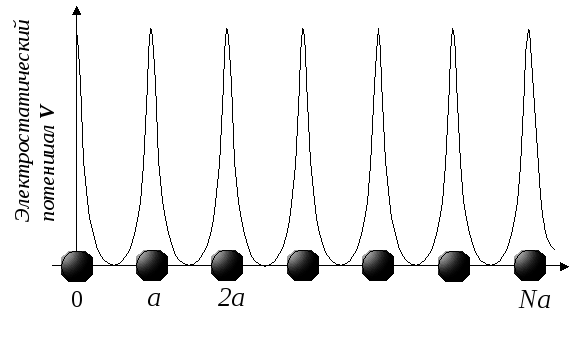
Независимые электроны, каждый из которых подчиняется одноэлектронному уравнению Шредингера с периодическим потенциалом, называют блоховскими, (в отличие от «свободных», к которым блоховские электроны сводятся, если периодический потенциал тождественно равен нулю).