
- •Федеральное агентство по образованию
- •Глава 1
- •1.1. Свободный электронный газ Ферми
- •1.2. Теплоемкость вырожденного электронного газа
- •1.3. Квантовая теория спинового парамагнетизма
- •1.4. Модель металлической проводимости
- •1.5. Плазменные колебания электронного газа
- •1.6. Свободные электроны в магнитном поле
- •Глава 2
- •2.1. Уравнение Шредингера для твердого тела
- •2.2. Теорема Блоха
- •2.3. Приближение почти свободных электронов
- •2.4. Приближение сильно связанных электронов
- •2.5. Зоны Бриллюэна
- •2.6. Число состояний электронов
- •2.7. Квазиимпульс
- •2.8. Движение электронов в кристалле под
- •2.9. Эффективная масса
- •2.10. Электроны и дырки
- •2.11. Металлы, диэлектрики, полупроводники
- •2.12. Энергетические уровни локальных и
- •2.13. Энергетический спектр некристаллических
- •Глава 3
- •Глава 1. Квантовая теория свободных электронов
- •Глава 2. Зонная теория твердых тел
- •Глава 3. Статистика электронов и дырок в полупроводниках
2.2. Теорема Блоха
Пространственная
зависимость потенциала, действие
которого испытывает в кристалле внешний
электрон, была рассмотрена Феликсом
Блохом. Согласно теореме Блоха, собственные
функции волнового уравнения с периодическим
потенциалом имеют вид произведения
функции плоской волны
![]() на функцию
на функцию![]() ,
которая является периодической функцией
в кристаллической решетке:
,
которая является периодической функцией
в кристаллической решетке:
![]() ,
(2.8)
,
(2.8)
где
![]() для всех
для всех![]() ,
принадлежащих решетке Браве.
,
принадлежащих решетке Браве.
Волновую функцию в виде (2.8) называют функцией Блоха. Решения уравнения Шредингера такого вида состоят из бегущих волн; из таких решений можно составить волновой пакет, который будет представлять электрон, свободно распространяющийся в периодическом потенциальном поле.
Запишем условия периодичности потенциальной энергии электрона в кристалле
![]() ,
(2.9)
,
(2.9)
где
вектор трансляции
![]() (
(![]() - векторы единичных трансляций;
- векторы единичных трансляций;![]() ,
,![]() ,
,![]() - произвольные целые числа). Из условия
(2.9) следует, что точки
- произвольные целые числа). Из условия
(2.9) следует, что точки![]() и
и![]() физически эквивалентны. Следовательно,
если в уравнении Шредингера заменить
физически эквивалентны. Следовательно,
если в уравнении Шредингера заменить![]() на
на![]() ,
то новая волновая функция электрона
,
то новая волновая функция электрона![]() будет отличаеться от волновой функции
будет отличаеться от волновой функции![]() некоторым постоянным множителемС,
т.е.
некоторым постоянным множителемС,
т.е.
![]() ,
(2.10)
,
(2.10)
Условия нормировки
![]() (2.11)
(2.11)
для
волновой функции
![]() имеет вид
имеет вид
![]() , (2.12)
, (2.12)
откуда
следует, что
![]() .
Это означает, чтоС
или равна единице, или мнимой экспоненте.
Учитывая, что волновая функция отражает
прохождение электронной волны в
кристалле, примем
.
Это означает, чтоС
или равна единице, или мнимой экспоненте.
Учитывая, что волновая функция отражает
прохождение электронной волны в
кристалле, примем
![]() .
.
Таким образом, влияние периодического поля решетки на волновую функцию свободного электрона выражается в появлении дополнительного множителя перед значением функции
![]() .
(2.13)
.
(2.13)
Тогда
![]() т.е. среднее распределение электронов
в решетке обладает пространственной
периодичностью.
т.е. среднее распределение электронов
в решетке обладает пространственной
периодичностью.
Рассмотрим теперь вид решения уравнения Шредингера для электрона в периодическом поле кристалла. Выражение (2.10) перепишем в виде
![]() ,
(2.14)
,
(2.14)
откуда с учетом (2.8) будем иметь
![]() ,
(2.15)
,
(2.15)
где
![]() .
(2.16)
.
(2.16)
Функция
![]() обладает периодичностью решетки, так
как согласно (2.14) и (2.16) имеем
обладает периодичностью решетки, так
как согласно (2.14) и (2.16) имеем
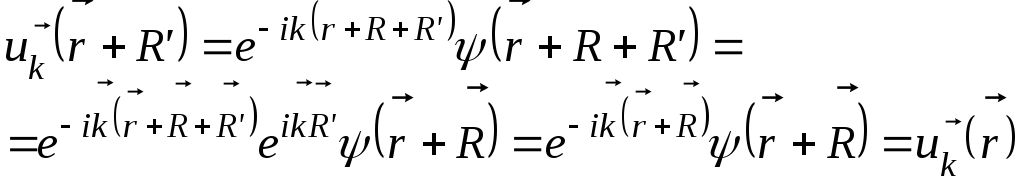 (2.17)
(2.17)
Таким образом, волновая функция электрона в кристалле представляет собой бегущую волну, модулированную по амплитуде с периодичностью решетки кристалла.
Если функцию Блоха (2.8) подставить в одноэлектронное уравнение Шредингера, то будем иметь
![]() ,
(2.18)
,
(2.18)
откуда
следует, что энергия электрона в кристалле
должна зависеть от волнового вектора
![]() ,
т.е.
,
т.е.![]() - закон дисперсии электрона в кристалле.
Отыскание вида
- закон дисперсии электрона в кристалле.
Отыскание вида![]() наряду с
наряду с![]() является основной задачей зонной теории
твердых тел.
является основной задачей зонной теории
твердых тел.
2.3. Приближение почти свободных электронов
Нахождение
собственных функций
![]() и собственных значений
и собственных значений![]() в уравнении Шредингера (2.8) в значительной
мере зависит от вида периодического
потенциала
в уравнении Шредингера (2.8) в значительной
мере зависит от вида периодического
потенциала
![]() .
В рамках одноэлектронного приближения
нахождение вида функции
.
В рамках одноэлектронного приближения
нахождение вида функции
![]() реальных кристаллов является практически
неразрешимой задачей. Поэтому приходится
прибегать к различным приближенным
методам расчета энергетического спектра
твердых тел, основанным на различных
подходах относительно вида потенциала
реальных кристаллов является практически
неразрешимой задачей. Поэтому приходится
прибегать к различным приближенным
методам расчета энергетического спектра
твердых тел, основанным на различных
подходах относительно вида потенциала
![]() .
.
Модель
почти свободных электронов для электронных
состояний в твердом теле применима,
когда периодический потенциал
![]() сравнительно мал. Современные теоретические
и экспериментальные исследования
металлов показывают, что в них для
описания движения электронов проводимости
можно использовать почти постоянный
потенциал. Такие элементы часто называют
металлами с «почти свободными электронами».
Отправной точкой при их описании служит
газ свободных электронов, свойства
которого изменены из-за присутствия
слабого
периодического потенциала. На основе
этой модели часто можно объяснить как
общие черты зонной структуры, так и
тонкие детали формы наблюдаемых
поверхностей Ферми.
сравнительно мал. Современные теоретические
и экспериментальные исследования
металлов показывают, что в них для
описания движения электронов проводимости
можно использовать почти постоянный
потенциал. Такие элементы часто называют
металлами с «почти свободными электронами».
Отправной точкой при их описании служит
газ свободных электронов, свойства
которого изменены из-за присутствия
слабого
периодического потенциала. На основе
этой модели часто можно объяснить как
общие черты зонной структуры, так и
тонкие детали формы наблюдаемых
поверхностей Ферми.
В
теории свободных электронов волновая
функция
![]() определяется плоской волной де Бройля
определяется плоской волной де Бройля![]() ,
а энергия и импульс электрона связаны
законом дисперсии
,
а энергия и импульс электрона связаны
законом дисперсии
![]() .
(2.19)
.
(2.19)
В
этом случае энергия электрона является
непрерывной функцией волнового вектора
![]() .
.
Такая
простота зависимости
![]() утрачивается, как только переходим к
собственным функциям уравнения
Шредингера, их волновым векторам и
разрешенным значениям энергии в случае
конечного периодического потенциала
утрачивается, как только переходим к
собственным функциям уравнения
Шредингера, их волновым векторам и
разрешенным значениям энергии в случае
конечного периодического потенциала
![]() .
Для нахождения зависимости
.
Для нахождения зависимости
![]() достаточно рассматривать случай малого
возмущения и применить обычные методы
теории возмущения. Возмущением при этом
является конечный потенциал
достаточно рассматривать случай малого
возмущения и применить обычные методы
теории возмущения. Возмущением при этом
является конечный потенциал
![]() .
.
Дальнейшее решение задачи сводится к нахождению поправок к энергии нулевого приближения (2.19) , которые определяются согласно теории возмущения матричными элементами оператора возмущения
![]() .
(2.20) Причем матричный элемент
.
(2.20) Причем матричный элемент![]() отличен
от нуля только при определенных значениях
состояний
отличен
от нуля только при определенных значениях
состояний![]() и
и![]()
 ,
(2.21)
,
(2.21)
где
![]() - коэффициенты ряда Фурье при разложении
в ряд потенциала
- коэффициенты ряда Фурье при разложении
в ряд потенциала
![]() по векторам обратной решетки
по векторам обратной решетки
![]() .
.
Согласно
теории возмущений энергия электрона в
кристалле при учете малого возмущения
![]() составляет
составляет
![]() . (2.22)
. (2.22)
Отсюда
следует, что добавка к энергии
![]() играет существенную роль при
играет существенную роль при
![]() ,
(2.23)
,
(2.23)
что
соответствует вырождению, так как одной
и той же энергии соответствуют два
значения волновой функции
![]() и
и![]() .
В этом случае волновую функцию уже в
нулевом приближении нужно искать для
вырожденных состояний в виде линейной
комбинации волновых функций
.
В этом случае волновую функцию уже в
нулевом приближении нужно искать для
вырожденных состояний в виде линейной
комбинации волновых функций![]() и
и![]() .
.
Решение этой задачи в квантовой механике дает следующее выражение для поправки к энергии электрона во втором приближении
![]() .
(2.24)
.
(2.24)
Как
следует из уравнения (2.24), энергия терпит
разрыв в точках, где выполняется условие
(2.23), и величина этого разрыва равна
![]() ,
т.е на границах зон Бриллюэна.
,
т.е на границах зон Бриллюэна.
Таким
образом, под действием периодического
потенциала параболический закон
дисперсии для свободного электрона
превращается в возмущенный энергетический
спектр. Отклонения от дисперсионного
закона для свободных электронов заметны
только в областях
![]() -пространства
вблизи границ зоны Бриллюэна.
-пространства
вблизи границ зоны Бриллюэна.
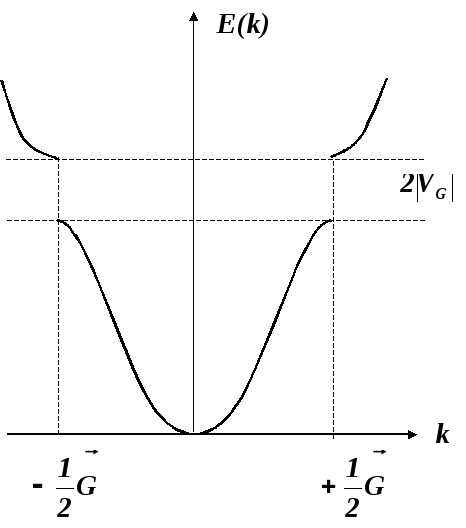
Из рис. 2.2 видно, что некоторым значениям энергии могут не соответствовать никакие электронные состояния, иначе говоря в энергетическом спектре могут появиться щели. Электронные уровни энергии образуют энергетические зоны. Это фундаментальное свойство; оно обуславливает многие другие свойства твердых тел. Природа его - в брегговском отражении. На электронные волновые функции «накладывается» периодичность решетки, что и приводит к расщеплению энергии.
Р
Рис.
2.2. Зависимость энергии электрона от
волнового вектора в одномерном случае
при конечной амплитуде периодического
потенциала.
![]() на границе зоны, так что уровень энергии
оказывается над одной из щелей или под
ней. Для одномерного случая это означает,
что
на границе зоны, так что уровень энергии
оказывается над одной из щелей или под
ней. Для одномерного случая это означает,
что![]() .
.
Условие
Брегга для электронов имеет вид
![]() и описывает дифракцию электронных волн
с волновым вектором
и описывает дифракцию электронных волн
с волновым вектором![]() .
Таким образом, валентные электроны
испытывают дифракцию на решетке так
же, как и электроны, падающие извне.
.
Таким образом, валентные электроны
испытывают дифракцию на решетке так
же, как и электроны, падающие извне.
Отражение
при
![]() получается, когда электронная волна от
данного атома линейной цепочки
интерферируют с волной от атома,
являющегося его ближайшим соседом.
Разность фаз между двумя волнами равнаπ.
Следовательно, решение для этого значения
получается, когда электронная волна от
данного атома линейной цепочки
интерферируют с волной от атома,
являющегося его ближайшим соседом.
Разность фаз между двумя волнами равнаπ.
Следовательно, решение для этого значения
![]() содержат две равные компоненты,
представляющие собой волну,
распространяющуюся влево (
содержат две равные компоненты,
представляющие собой волну,
распространяющуюся влево (![]() )
и вправо (
)
и вправо (![]() ).
При этом волновые функции электрона не
являются бегущими волнами типа
).
При этом волновые функции электрона не
являются бегущими волнами типа![]() ,
а являются стоячими волнами.
,
а являются стоячими волнами.
Чтобы
лучше понять происходящее, найдем
волновые функции в точке
![]() .
Из бегущих волн
.
Из бегущих волн
![]() и
и
![]() можно сформировать две различные стоячие
волны:
можно сформировать две различные стоячие
волны:
![]() ,
(2.25)
,
(2.25)
![]() .
(2.26)
.
(2.26)
Две
стоячие волны
![]() и
и![]() отвечают группировке электронов в
различных по отношению к ионам областям
пространства, а, следовательно, эти две
волны имеют различные значения
потенциальной энергии. Это и есть причина
образования энергетической щели.
отвечают группировке электронов в
различных по отношению к ионам областям
пространства, а, следовательно, эти две
волны имеют различные значения
потенциальной энергии. Это и есть причина
образования энергетической щели.
Действительно,
функция
![]() велика вблизи точки
велика вблизи точки![]() ,
а также вблизи любого узла цепочки
атомов. Она описывает состояние, в
котором электроны сконцентрированы
вблизи атомов (рис.2.3). Энергия в состоянии
с волновой функцией
,
а также вблизи любого узла цепочки
атомов. Она описывает состояние, в
котором электроны сконцентрированы
вблизи атомов (рис.2.3). Энергия в состоянии
с волновой функцией![]() понижена по сравнению с энергией
свободного электрона на величину
понижена по сравнению с энергией
свободного электрона на величину![]() за счет захвата электрона потенциальными
ямами атомов
за счет захвата электрона потенциальными
ямами атомов
![]() .
(2.27)
.
(2.27)
Подобным
же образом энергия в состоянии с волновой
функцией
![]() увеличена, так как теперь плотность
электронов больше в областях с
положительным потенциалом (рис.2.3)
увеличена, так как теперь плотность
электронов больше в областях с
положительным потенциалом (рис.2.3)
![]() .
(2.28)
.
(2.28)
Т
Рис.
2.3. Периодический потенциал и концентрация
электронов в состояниях, описываемых
волновыми функциями
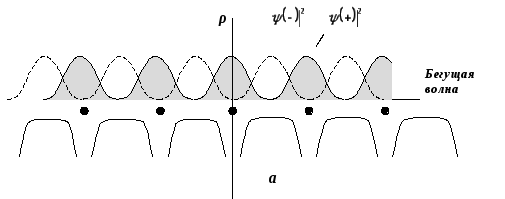
![]() и
и![]() .
.![]() .
.
Отметим,
что закон дисперсии, показанный на
рис.2.2, соответствует изменению
волнового вектора вдоль какого-то
одного направления в
Рис.
2.4. Закон дисперсии
![]() -пространстве.
Аналогичные зависимости можно построить
и в двух других направлениях, причем
качественный характер
-пространстве.
Аналогичные зависимости можно построить
и в двух других направлениях, причем
качественный характер![]() не зависит от направления. Однако
величины трансляции в различных
направлениях по высоте могут как
перекрываться, так и н
не зависит от направления. Однако
величины трансляции в различных
направлениях по высоте могут как
перекрываться, так и н
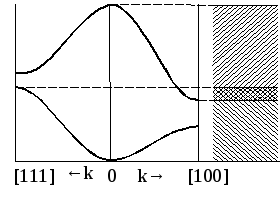
![]() вдоль направлений [100] и [111].
вдоль направлений [100] и [111].
