1.6. Свободные электроны в магнитном поле

Для модели свободных электронов в отсутствии магнитного поля решения уравнения Шредингера (1.1) представляют собой плоские волны, волновые вектора которых связаны с собственными значениями энергии электрона соотношением

. (1.49)

Рассмотрим динамику электронного газа в постоянном магнитном поле . Положим, что магнитное поле направлено по осиz. Известно, что магнитное поле В_z будет оказывать действие на движение электрона в плоскости ху, оставляя невозмущенным его движение в z-направлении. Сила Лоренца превращает движение электрона в сумму прямолинейного движения в направлении z и циклотронного движения в плоскости ху. Таким образом, электрон движется по спиральной траектории.

Из теории электромагнитного поля известно, что вектор индукции магнитного поля связан с векторным потенциаломсоотношением . В нашем случае магнитное поле имеет одну z- компоненту , а его вектор-потенциал – толькоy- компоненту.

Электрон с зарядом - е и импульсом , при прохождении в области действия поля, определяемого векторным потенциалом, будет иметь обобщающий импульс . Функция гамильтона электрона для этого случая запишется в виде

, (1.50)

Переходя от функции Гамильтона к оператору Гамильтона, уравнение Шредингера будет иметь вид

. (1.51)

Поскольку сила Лоренца не имеет составляющей в направлении , поле не оказывает влияния на энергию движения в этом направлении и она остается равной. Но для определения характера движения в плоскости (x,y) надо решить уравнение (1.51). Решение этого уравнения следует искать в виде суперпозиции

, (1.52)

где - некоторая функция, зависящая только отх.

При подстановке (1.52) в (1.51) получим для уравнение

. (1.53)

Введем обозначения: ;;.

Теперь уравнение (1.53) принимает вид

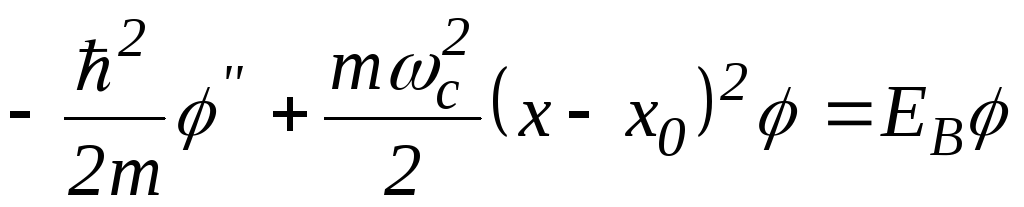. (1.54)

Оно формально совпадает с уравнением Шредингера для одномерного осциллятора, колеблющегося вокруг с частотой.

Собственные значения энергии электрона будут равны

, ,. (1.55)

Энергия электрона представлена в виде суммы энергии поступательного движения вдоль магнитного поля (по z) и квантованной энергии циклотронного движения в перпендикулярной плоскости (ху). Для данного значения квантового числа n циклотронное движение происходит по траектории с радиусом

. (1.56)

Отождествляя сисможно видеть, что электронная прецессия в - пространстве должна удовлетворять условию

. (1.57)

Таким образом, все состояния, соответствующие данному значению n, попадают в -пространстве на цилиндрическую поверхность радиусом

. (1.58)

Э

Рис. 1.5. Влияние магнитного поля на области -пространства, которые могут быть заняты электронами. Разрешенные состояния образует ряд бесконечных коаксиальных цилиндров, параллельных .

та ситуация, представленная на рисунке 1.5, коренным образом отличается от однородного распре­деления электронов в -простран­стве в отсутствии магнитного поля. Совокупность электронных состоя­ний, соответствующих данному зна­чению квантового числа n, называют магнитной подзоной, или уровнем Ландау.

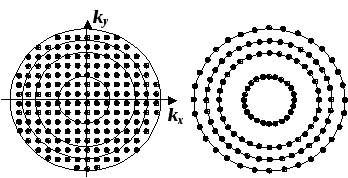
Таким образом, влияние магнитного поля сводится к тому, что оно создает квантованные орбиты в -пространстве и заставляет свободные электроны «конденсироваться» на ближайших орбитах (см. рис. 1.6). Число состояний на каждой орбите точно равно числу прежних состояний в кольце, в котором лежит орбита.

Де Гааз и Ван-Альфен в 1930 г. обнаружили осциллирующую зависимость от поля магнитной восприимчивости.

Н

B = 0

Рис. 1.6. Схема квантования для свободных электронов.

аличие ярко выраженной осцилляторной структуры в плотности электронных уровней в магнитном поле является первопричиной осцилляций де Гааза-ван-Альфена и связанных с ними эффектов.

П

Рис. 1.7. Плотность состояний свободных электронов как функция энергии при наличии большой магнитной индукции. D₀(E) – плотность состояний в отсутствии магнитного поля.

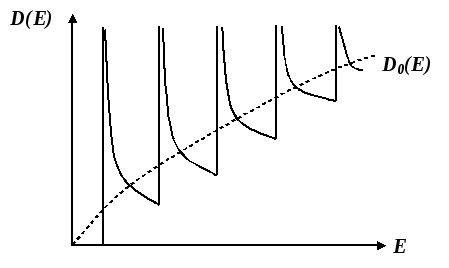
роисхождение эффекта легко понять, учитывая разрывную плотность состоянийэлектронов в магнитном поле (рис. 1.7).

Сходное осциллирующее поведение обнаруживает не только восприимчивость, но и проводимость (эффект Шубникова – де-Гааза), магнитострикция и практически все другие величины при тщательном их измерении.