2.10. Электроны и дырки

Из (2.77) следует, что эффективная масса блоховских электронов в энергетической зоне определяется кривизной поверхности в-пространстве: чем больше эта кривизна, тем меньше эффективная масса.

Анализ дисперсионной зависимости (2.65) в модели сильной связи показывает, что для электронов, располагающихся у дна энергетической зоны

, (2.79)

т.е. эффективная масса m* положительна. Вблизи максимумов, т.е. у потолка зоны

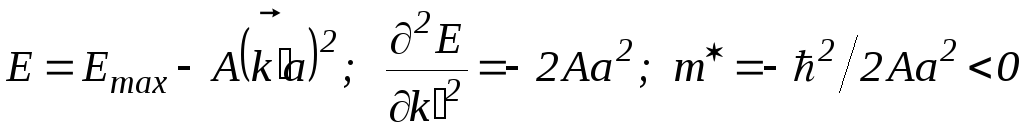, (2.80)

где вектор , эффективная масса m* оказывается отрицательной. Поскольку масса не может быть отрицательной, то для состояний у верхнего края энергетической зоны вводится понятие дырки, рассматривая ее как квазичастицу с положительной эффективной массой, но и с положительным зарядом +е. Такая частица будет перемещаться по кристаллу по направлению действия внешней силы.

Главной особенностью дырки является то, что ее скорость совпадает со скоростью недостающего энергетического состояния в зоне; волновой пакет будет двигаться с той же скоростью, что и его соседи со всех сторон от дырки.

Поэтому, если считать, что ток переносится не электронами, а дырками, то электроны лучше всего рассматривать как отсутствие дырок; уровни, занятые дырками, есть уровни, не занятые дырками. Состояния, свободные от электронов, находятся в самой верхней части зоны, т.е. дырки располагаются у потолка зоны, где их энергия минимальна. Следовательно, энергия дырок отсчитывается в направлении, противоположном отсчету энергии для электрона.

Дырки простым способом описывают движение большого числа электронов в кристалле при почти заполненной зоне. Действительно, если из почти заполненной энергетической зоны удален один электрон, плотность тока в электрическом поле составит

, (2.81)

где - плотность тока в полностью заполненной зоне, поскольку каждому электрону с квазиимпульсомв ней можно сопоставить электрон с квазиимпульсоми с то же энергией.

Следовательно, плотность тока, создаваемая электронами зоны с одним незаполненным состоянием, равна по величине и противоположна по направлению плотности тока, создаваемой недостающим электроном.

Плотность тока, связанная с одним электроном (n = 1), равна

. (2.82)

Так как , имеем

. (2.83)

Это та плотность тока, которая создавалась бы частицей с массой и зарядомe. Фактически движутся, естественно, электроны. Однако электрон у потолка зоны движется против действия силы. По это причине удаление такого электрона приводит к увеличению плотности тока, такому, как если бы появилась частица с положительной массой и положительным зарядом.

Отметим еще раз: эффективная масса m* отражает способность электрона у дна зоны или дырки у ее потолка реагировать на внешнее поле, действующее совместно с межатомным периодическим потенциалом

2.11. Металлы, диэлектрики, полупроводники

в зонной теории

Рассмотрим теперь, как зонная теория твердого тела объяс­няет физические свойства реальных веществ и прежде всего раз­личие этих свойств для металлов, полупроводников и диэлек­триков.

Определим валентную зону как наивысшую энергетическую зону в твердом теле, которая целиком заполнена электронами в основном состоянии (при Т=0), зону проводимости - как самую нижнюю энергетическую зону в твердом теле, которая содержит свободные уровни в основном состоянии (незаполненную или содержащую некоторое число носителей при Т=0).

Рассмотрим случай, когда зона проводимости отделена от валентной зоны энергетической щелью E_g (рис.2.12). Пусть при Т=0 все состояния в зоне проводимости свободны, а в валентной зоне полностью заполнены электронами. В таком кристалле требуется конечная энергия возбуждения, больше ширины запрещенной зоны E_g, для перевода электронов вверх через энергетическую щель в зону проводимости. Если ширина запрещенной зоны E_g велика, так что ни температура, ни постоянное электрическое поле (и другие воздействия, которые не разрушают твердое тело) не могут сообщить электронам достаточную энергию для перехода в зону проводимости, то такое твердое тело не проводит электрический ток и я

Рис. 2.12. Схема энергетических зон металла (а), полупроводника (б), полуметалла (в) и диэлектрика (г)

вляетсядиэлектриком.

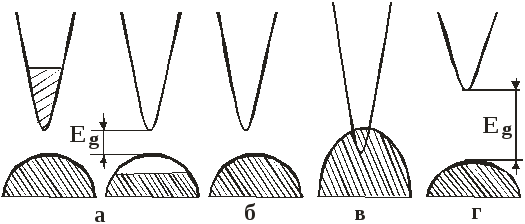
Ана­логичный вывод мы получим, если рассмотрим полностью свобод­ную от носителей заряда разрешенную зону, так как при прило­жении электрического поля к такой зоне она не даст никакого вклада в электропроводность. Такой кристалл также будет диэлектриком.

Если ширина запрещенной щели невелика, то при конечной температуре T в результате тепловых флуктуаций некоторое число электронов, определяемое характерным больцмановским множителем, перейдет из валентной зоны в зону проводимости. Как электроны в зоне проводимости, так и дырки (свободные, незаполненные состояния), образовавшиеся в результате ухода электронов из валентной зоны, будут являться носителями тока и будут давать свой вклад в величину проводимости. Вещества с таким энергетическим спектром обладают конечной электропроводностью, быстро возрастающей с ростом температуры, называютсяполупроводниками.

Следовательно, в основном состоянии полупроводники не проводят тока, так как в основной разрешенной зоне все состояния заняты, и проводимость возникает только при сообще­нии электрону дополнительной энергии для перехода в незапол­ненную разрешенную зону. Значит, полупроводники и диэлек­трики относятся к одному типу веществ - между ними нет принципиальной разницы. Различие носит коли­чественный характер - по величине запрещенной зоны. Если эВ, то такие непроводники называют полупроводни­ками.

Удельное электросопротивление полупроводников при комнатной температуре лежит в интервале от 10^-6 до 10⁸ . По величине сопротивления они находятся между хорошими проводниками (~ 10^-8 – 10^-6 ) и изоляторами (>10⁸ ).

Если зона проводимости заполнена не полностью и электронов достаточно много, то концентрация носителей тока не будет зависеть от температуры. Такие вещества являются металлами. Металли­ческая проводимость образуется и при перекрытии заполненной энергетической зоны с незаполненной зоной.

Зная, что число состояний в зоне Бриллюэна определяется как 2N, т. е. по два состояния на элементарную ячейку в зоне, можно, подсчи­тывая число электронов, приходящихся на элементарную ячейку, классифицировать вещество на металлы, полупроводники и диэлектрики.

• Вещества, в которых на элементарную ячейку приходится один свободный электрон, являются металлами, так как электроны заполняют половину зоны. К ним относятся одновалентные щелочные металлы Li, Na, K, Rb, Cs и благородные металлы Cu, Ag, Au.

• Вещества, в которых на элементарную ячейку приходится нечетное число электронов, также будут металлами, как и в предыдущем случае. К ним относятся металлы Al, Ga, In, Tl, в которых на один атом приходится три электрона. При этом валентная энергетическая зона заполнена полностью, а зона проводимости - наполовину.

• Вещества, в которых на элементарную ячейку приходится четное число электронов, не обязательно будет изоляторами, так как энергетические зоны, как мы уже видели, могут перекрываться.

Элементы As, Sb, Bi, в которых на элементарную ячейку приходится по два атома, а каждый атом имеет пять электронов, представляют собой полуметаллы. Зонную структуру их можно рассматривать, как для полупроводников, однако минимум зоны проводимости лежит немного ниже максимума валентной зоны, т. е. разрешенные энергетические зоны перекрываются, и понятие запрещенной зоны теряет, как и для металла, смысл. С этим об­стоятельством и связано название полуметалла.

Все двухвалентные вещества - металлы с хорошей проводимостью, за исключением Sr и Br, которые являются плохими проводниками из-за слабого перекрытия зон. Четырехвалентный углерод существует или в виде алмаза, со столь широкой запрещенной зоной, что его практически можно считать изолятором или в виде графита, являющегося полуметаллом. Кремний и германий - типичные полупроводники. Олово в одной фазе представляет собой металл, а в другой - полупроводник. Свинец - типичный металл.