92

Федеральное агентство по образованию

Дагестанский государственный университет

Садыков С.А.

ФИЗИКА ТВЕРДОГО ТЕЛА

Электронная структура

кристаллов

Махачкала

ИПЦ ДГУ

2007

Издается по решению редакционно-издательского совета Дагестанского государственного университета.

Садыков С.А. Физика твердого тела. Электронная структура кристаллов. Махачкала, ИПЦ ДГУ, 2007. 96 с.

Учебное пособие по физике твердого тела предназначено для студентов высших учебных заведений, обучающихся по направлению «Электроника и микроэлектроника», по специальностям «Микроэлектроника и твердотельная электроника», «Физическая электроника», а также для студентов старших курсов физических специальностей университетов.

В учебном пособии рассматриваются основы квантовой теории электронов в металлах, обсуждается зонная теория твердых тел и на ее основе статистика электронов в полупроводниках.

Рецензенты:

Каллаев С.Н. - д.ф.м.н., зав. лабораторией ИФ ДНЦ РАН

Митаров Р.Г. - д.ф.м.н., проф. кафедры физики ДГТУ

Глава 1

Квантовая теория свободных

электронов

1.1. Свободный электронный газ Ферми

Свободные электроны в металле обладают резко выраженными квантовыми свойствами, главным из которых является то, что их энергия квантована и они подчиняются принципу запрета Паули (1925 г.). Газ свободных электронов, подчиняющихся принципу Паули, часто называют свободным электронным газом Ферми.

В квантовой теории металлов, которая была разработана Зоммерфельдом в результате использования принципа Паули, была принята та же модель идеального газа свободных независимых электронов, что и в классической теории Друде. Существенное отличие состояло в том, что скорости электронов после столкновений теперь определяются не классической статистикой Максвелла-Больцмана, а квантовой статистикой Ферми-Дирака.

Рассмотрим вкратце основные положения этой статистики и некоторые следствия из нее для свободных независимых электронов. Для свободного электрона, потенциальная энергия которого произвольно положена равной нулю, полная энергия совпадает с его кинетической энергией. Тогда оператор полной энергии или гамильтониан превращается в оператор только кинетической энергии и уравнение Шредингера для свободного электрона будет иметь вид

, (1.1)

где Е – энергия электрона в состоянии, описываемом волновой функцией ,- оператор Лапласа,m – масса электрона.

Если электроны заключены в ограниченном объеме со стороной L, то решениями волнового уравнения (1.1), удовлетворяющими периодическим граничным условиям Борна-Кармана

(1.2)

являются волновые функции, имеющие вид плоской волны

(1.3)

где ,,;,,– вещественные целые числа.

Теперь могут быть определены как квантовые числа, задающие состояние электрона наряду со спином; -векторы в уравнении (1.3) могут быть представлены в виде точечной решетки в -пространстве. Каждой -точке соответствует два одночастичных состояния с противоположными спинами. Каждое состояние, по принципу Паули, может быть занято одним электроном.

Пусть число электронов в основной области N. Состояние наименьшей энергии электронного газа (основное состояние) тогда будет описываться тем, что точек наиболее низких энергий будет занято двумя электронами каждая (рис. 1.1). В -пространстве эти точки заполнят шар с радиусом (сфера Ферми), объем которого равен. Так как каждой -точке соответствует объем в -пространстве, то объем сферы Ферми составит таких объемов

(1.4)

И

Рис. 1.1. Некоторые из разрешенных точек в k-пространстве для циклических граничных условий с периодом L для каждого из направлений в реальном пространстве.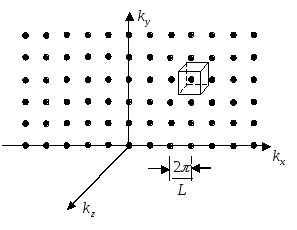

з этого условия следует

. (1.5)

Тогда электроны на поверхности сферы Ферми имеют энергию

, (1.6)

где ,n – концентрация электронов.

Возбуждение электрона в состояние с более высокой энергией приводит к его выходу из сферы Ферми. Основное состояние ферми-газа – это полностью заполненная электронами сфера Ферми. В этом случае функция распределения, т.е. вероятность того, что состояние с энергией Е занято частицей, , если;, если, где- определяется количеством электронов в системе.

В термодинамическом равновесии для частиц с полуцелым спином, подчиняющихся принципу Паули, в 1926 г. Ферми и независимо от него Дирак нашли вид функции распределения по энергиям

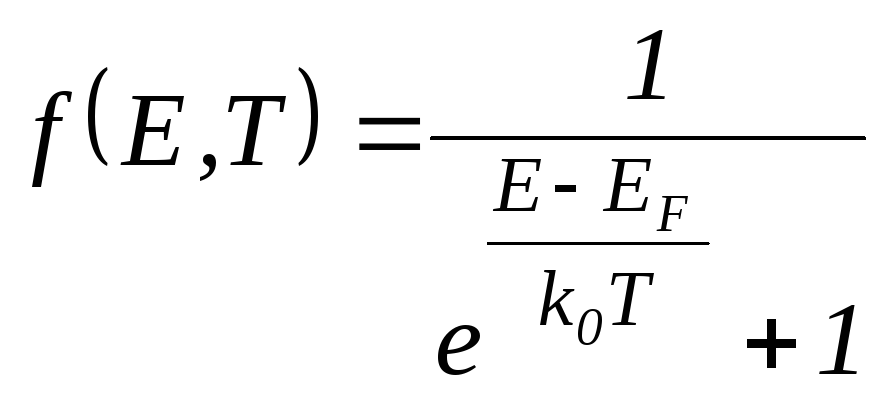. (1.7)

Из (1.7) следует, что в случае в интервале энергийимеемидля(рис. 1.2). Это означает, что все квантовые состояния с энергией, заняты электронами, а уровни, лежащие выше уровня Ферми, полностью свободны. Следовательно,энергия Ферми есть максимально возможная энергия электронов в металле при . Уровень, соответствующийи отделяющий полностью заполненные уровни от полностью незаполненных, называют уровнем Ферми.

П

Рис. 1.2 Функция распределения Ферми-Дирака.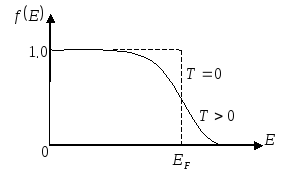

ридля значений энергииимеем. Таким образом, уровень Ферми есть энерге­тический уровень, вероят­ность заполнения которого при температуре, отличной от абсолютного нуля, равна. Возбуждение электронов в состоя­ние с более высокой энергией приводит к размытию границы ме­жду занятыми и незанятыми состояниями.

Положение уровня Ферми при можно определить из условия, что полное число электронов проводимости должно оставаться неизменным при любой температуре

, (1.8)

где - плотность состояний, т.е. число состояний электронов на единичный энергетический интервал. С учетом (1.5) дляполучим

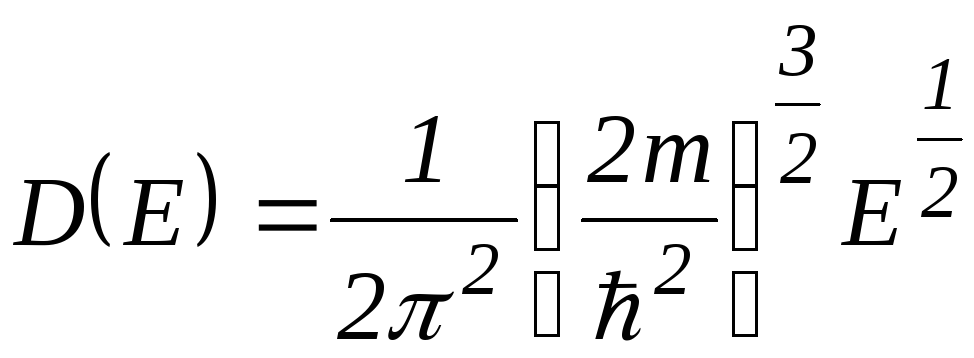. (1.9)

Подставив (1.9) в (1.8), получим при T = 0

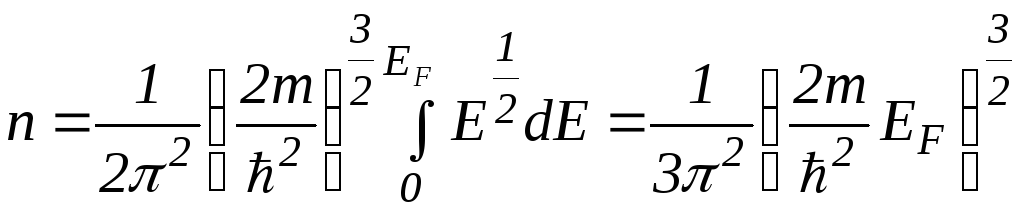. (1.10)

Величина очень мало уменьшается с повышением температуры относительно значения при 0К

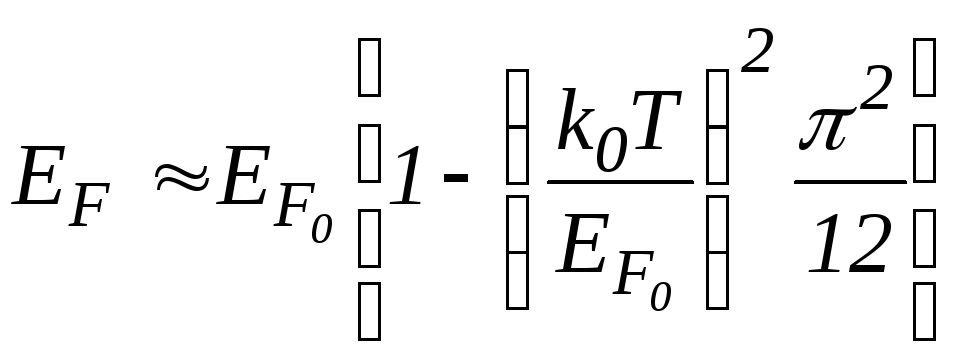. (1.11)

Поэтому в дальнейшем будем говорить об энергии Ферми , не указывая температуру, к которой она относится.

Сравним далее распределение по состояниям, задаваемой функцией распределения Ферми-Дирака (1.7), с классическим распределением, описываемым функцией Максвелла-Больцмана:

, (1.12)

где А – некоторая нормировочная константа этого распределения.

Если положить и пренебречь единицей в знаменателе (1.7), получим

. (1.13)

Таким образом, при выполнении критерия функцию распределения Ферми-Дирака можно приближенно заменить классической функцией Максвелла-Больцмана. Система электронов, для которой этот критерий выполняется, называютневырожденной.

Если такое приближение применить нельзя, то система называется вырожденной и описывается функцией распределения Ферми-Дирака.