
- •§ 4. Линейные дифференциальные уравнения высших порядков
- •§ 5. Линейные однородные уравнения
- •§ 6. Линейное однородное уравнение с постоянными коэффициентами
- •§ 7. Линейные неоднородные уравнения
- •§ 10. Интегрирование дифференциальных уравнений с помощью рядов
- •§ 12. Краевые задачи в линейных дифференциальных уравнениях
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Литература
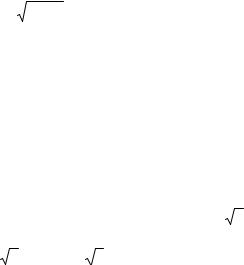
Пример 1. Найти общее решение уравнения Эйлера x2 y′′ + |
5xy′ + |
4 y = |
0. |
Решение. Будем искать решение уравнения Эйлера в виде y = |
xr , |
то- |
|
гда получим: x2 r(r − 1)xr− 2 + 5xrxr− 1 + 4xr = 0, r(r − 1) + 5r + 4 = 0, r 2 + |
4r + 4 = |
0, |
|
r1 = r2 = − 2 - двукратный корень характеристического уравнения. Поэтому общее решение имеет вид: y = C1 x− 2 + C2 x − 2 ln x.
Пример 2. Найти общее решение уравнения Чебышева
y′′ = |
d 2 y |
= |
|
dx2 |
|||
|
|
|
(1 − x 2 ) y′′ − xy′ + 4 y = 0 ( |
|
x |
|
< 1). |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x = cos t |
(t |
(0,π |
)), |
тогда |
|
|
|
|
||||||||||||||||
|
|
y′ |
|
dy |
|
|
|
dy |
|
dt |
|
dy |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
= |
|
= |
|
|
|
|
= |
|
|
|
− |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
dx |
|
dt |
dx |
|
|
sint |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
d |
dy |
|
|
1 |
|
|
dt |
|
|
d 2 y |
|
|
|
1 |
|
|
dy |
|
cost |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
dx |
= |
|
|
dt |
2 |
− |
|
|
|
|
|
|
+ |
dt |
|
2 |
|
|
× |
||||
dt |
dt |
sint |
|
|
|
|
|
|
sint |
|
|
|
sin |
|
t |
|
|||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
d 2 y |
|
1 |
|
|
|
dy |
|
|
cost |
, |
|
|
|
|
|
|
|||||||||
× |
|
|
− |
|
|
|
|
= |
|
|
|
2 |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
dt |
sin |
2 |
t |
dt |
sin |
3 |
t |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
получим |
|
d 2 y |
|
+ 4 y = |
0 , |
|
|
откуда |
y = C cos 2t + |
C |
|
sin 2t = |
C cos(2arccos x) + |
|||||||||||||
|
dt2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
1 |
|
|||
+ C |
2 |
sin(2arcsin x) = |
C (2x2 − |
1) + 2C |
2 |
x 1− |
x2 . |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Пример 3. Найти общее решение уравнения |
y′′ + 2xy′ + |
(x2 + |
6) y = 0. |
|||||||||||||||||||||
|
|
Решение. Имеем уравнение вида (21). Найдем Q(x) : |
|
|
||||||||||||||||||||||
|
|
|
|
Q(x) = a2 (x) − |
|
1 |
a12 (x) − |
1 |
a1′(x) = x2 + 6 − |
1 |
4x2 − |
1 |
2 = 5 . |
|
||||||||||||
|
|
|
|
4 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
4 |
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Заменой |
y = u exp − |
|
∫ 2xdx |
данное уравнение |
сводится к |
уравнению |
||||||||||||||||||||
2 |
||||||||||||||||||||||||||
u′′ + |
|
5u = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Составим характеристическое уравнение k 2 + 5 = |
0, |
|
k1,2 = ± |
5i. Общее реше- |
||||||||||||||||||||||
ние запишется |
y = e− |
|
x2 |
(C1 cos |
|
5x + |
C2 sin 5x). |
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
§10. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ
В некоторых случаях, когда интегрирование дифференциального уравнения в элементарных функциях невозможно, решение такого уравнения ищут в виде степенного ряда
y = ∑∞ |
cn (x − x0 )n . |
(22) |
n= 0 |
|
|
28
Неопределенные коэффициенты cn (n = 0, 1, 2, Κ ) находят подстановкой ряда в дифференциальное уравнение и приравниванием коэффициентов
при одинаковых степенях разности (x − |
x0 ) |
в обеих частях полученного ра- |
|||||||||||||||
венства. |
Если удается найти все коэффициенты ряда, то полученный ряд |
||||||||||||||||
определяет решение во всей своей области сходимости. |
|
|
|
||||||||||||||
В тех случаях, когда для уравнения |
y′ = |
f (x, y) требуется решить задачу |
|||||||||||||||
Коши при начальных условиях |
y |
|
x= x0 |
= |
y0 , решение можно искать с помо- |
||||||||||||
|
|||||||||||||||||
|
|
||||||||||||||||
щью ряда Тейлора: y = ∑∞ |
y (n) (x0 ) |
(x − |
x0 )n , |
где y(x0 ) = y0 , |
y′(x0 ) = |
f (x0 , y0 ), а |
|||||||||||
|
|||||||||||||||||
|
|
|
n= 0 |
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
дальнейшие производные |
y (n) (x0 ) находим последовательным дифферен- |
||||||||||||||||
цированием |
исходного |
уравнения |
и |
|
подстановкой |
вместо |
|||||||||||
′ |
значений x0 , y0 , |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
x, y, y , Κ |
y0 , Κ . |
|
|
|
|
|
|
|
|
|
|||||||
Аналогично с помощью ряда Тейлора можно интегрировать и уравне- |
|||||||||||||||||
ния высших порядков. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 1. Найти общее решение уравнения y′′ − x2 y = |
0. |
|
|||||||||||||||
Решение. |
Будем искать решение |
этого |
|
уравнения в |
виде ряда |
||||||||||||
y = C0 + C1x + C2 x2 + Κ |
+ Cn xn + Κ . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставляя y |
и y′′ |
в исходное уравнение, находим |
|
|
|
||||||||||||
|
[2 1C2 + 3 2C3 x + |
4 3C4 x2 + Κ |
+ (n + 2)(n + 1)Cn+ 1xn + |
Κ |
]− |
|
|||||||||||
|
|
|
|
|
|
|
|
− x2 |
[C |
0 |
+ C x + C |
2 |
x2 + Κ + C |
n |
xn + Κ ] ≡ 0. |
||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
Сгруппируем члены с одинаковыми степенями x : |
|
|
|
||||||||||||||
|
|
2 1C2 + 3 2C3 x2 + ∑∞ |
[(n + |
4)(n + |
3)Cn+ 4 |
− Cn]xn+ 2 ≡ |
0. |
|
|||||||||
|
|
|
|
|
n= 0 |
|
|
|
|
|
|
|
|
|
|||
Приравнивая к нулю все коэффициенты полученного ряда (чтобы уравне-
ние |
обратилось |
в |
тождество), |
находим |
C2 = |
C3 = 0; |
|||
Cn+ 4 = |
Cn |
|
(n = |
0,1, 2, Κ |
). Последнее соотношение позволяет найти по- |
||||
(n + 3)(n + |
4) |
||||||||
|
|
|
|
|
и C1 |
остаются |
|||
следовательно все коэффициенты искомого разложения (C0 |
|||||||||
произвольными и считаются произвольными постоянными интегрирования):
C4k = |
|
C0 |
; C4k + 1 = |
|
|
|
C1 |
; |
|
|
3 4 7 8 Κ |
|
(4k − 1) 4k |
4 5 8 9 Κ |
4k(4k + 1) |
|
|||||
C4k+ 2 = C4k + 3 = 0 (k = 0, 1, 2, Κ ). |
|
|
|
x4k+ 1 |
|
|
||||
|
∞ |
|
x4k |
|
∞ |
|
|
|
||
Таким образом, y = C0 ∑ |
|
|
|
|
+ C1 ∑ |
|
|
|
. |
|
|
3 4 7 8 Κ |
(4k − 1)4k |
|
4 |
5 8 9 Κ 4k(4k + 1) |
|||||
|
k = 0 |
|
|
k= 0 |
|
|||||
Полученные ряды сходятся на всей числовой оси и определяют два линейно независимых частных решения исходного уравнения.
29
Пример 2. Проинтегрировать приближенно с помощью ряда Тейлора
уравнение y |
′′ |
= x + y |
2 |
, y(0) = |
0, |
|
|
′ |
= 1. Найти четыре первых (отличных от |
|||||||||||||||
|
|
|
y (0) |
|||||||||||||||||||||
нуля) члена разложения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение. Дифференцируя уравнение y′′ = |
x + |
y 2 , имеем |
|
|||||||||||||||||||||
y′′′ = 1+ |
2yy′, |
y(4) = 2 yy′′ + 2 y′2 , |
|
y(5) = |
2 yy′′′ + |
6 y′y′′, |
y(6) |
= |
2 yy(4) + |
8y′y′′′ + 6 y′′2 . |
||||||||||||||
При x = |
0 получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y(0) = 0, |
y′(0) = 1, |
|
y′′(0) = 0, |
|
y′′′(0) = 1, |
y(4) (0) = |
2, |
|
y(5) (0) = |
0, |
y (6) (0) = 16. |
|||||||||||||
Решение имеет вид |
y = |
|
x |
+ |
x3 |
+ |
|
2x 4 |
+ |
16x5 |
+ Κ = x |
+ |
x3 |
+ |
x 4 |
+ |
x6 |
|
+ Κ . |
|||||
|
3! |
4! |
|
|
|
45 |
|
|||||||||||||||||
|
|
|
|
|
|
1! |
|
6! |
|
6 |
12 |
|
|
|
||||||||||
§11. УРАВНЕНИЕ БЕССЕЛЯ
Уравнением Бесселя называется дифференциальное уравнение вида
x2 y′′ + xy′ + (x2 − n2 ) y = 0, |
(23) |
где n = const .
Решение уравнения определяют в виде произведения некоторой степени x
на степенной ряд y = |
xr ∑∞ |
ak xk . |
|
|
|
|
k = 0 |
|
|
Коэффициент a0 |
мы можем считать отличным от нуля ввиду неопределен- |
|||
ности показателя x. |
|
|
|
|
Перепишем y = ∑∞ |
ak xr + k |
и найдем производные: |
||
k = |
0 |
|
|
|
y′ = ∑∞ |
(r + k)ak xr + k − 1 , y′′ =∑ ∞ |
(r + k)(r + k − 1)ak x r + k − 2 . |
||
|
k = 0 |
|
k = 0 |
|
Подставим эти выражения в уравнение (23):
x2 ∑∞ |
(r + k)(r + k − 1)ak x r + k − 2 + x∑∞ |
(r + k)ak xr + k − 1 + (x 2 − n2 )∑∞ |
ak xr + k = |
k = 0 |
k = 0 |
k = 0 |
|
Приравнивая к нулю коэффициенты при |
|||
получаем систему уравнений: |
|||
|
[r(r − 1) + r − n2]a0 = 0 |
|
|
|
[(r + 1)r + (r + 1) − n2]a1 = 0 |
||
|
|||
|
[(r + 2)(r + 1) + (r + 2) − n |
2 |
]a2 = 0 |
|
|
||
|
Λ Λ Λ Λ Λ Λ Λ Λ Λ Λ Λ Λ Λ Λ |
||
|
|||
|
[(r + k)(r + k − 1) + (r + k) − n2]ak + ak− 2 = 0 |
||
|
Λ Λ Λ Λ Λ Λ Λ Λ Λ Λ Λ Λ Λ Λ Λ Λ Λ |
||
|
|||
x в степени r, |
r + 1, |
r + |
2, Κ |
|||||||
|
|
(r 2 − n2 )a0 = 0 |
|
|
||||||
|
|
[(r + 1)2 − n2]a1 = 0 |
|
|||||||
|
|
|
||||||||
|
|
[(r + |
2) |
2 |
− |
n |
2 |
]a2 |
+ a0 |
= 0 |
, или |
|
|
|
|||||||
|
Λ |
Λ Λ |
Λ |
Λ |
Λ |
Λ Λ |
Λ |
|||
|
|
|||||||||
|
|
[(r + k)2 − n2 |
]ak + ak− 2 = |
|||||||
|
|
Λ Λ Λ Λ Λ Λ Λ Λ Λ Λ |
||||||||
|
|
|||||||||
0 .
, r + k ,
.
0
30
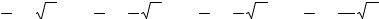
Рассмотрим равенство [(r + k)2 − |
n2 ]ak |
+ ak − 2 |
= |
0 . Его можно переписать |
в виде |
|
|
|
|
[(r + k − n)( r + k + n) ]ak + ak − 2 = 0 . |
|
|
|
|
По условию a0 ≠ 0 , следовательно, r 2 |
− n2 = |
0, r1 |
= |
n, r2 = − n . |
1. Пусть n не равно целому числу.
Из системы уравнений последовательно определяются все коэффициенты a1 , a2 ,...; a0 остается произвольным.
Пусть r=n, тогда a0 |
= 1, a1 = |
0 тогда |
|
ak = − |
k(2n + |
k) , k=(2,3,…). Придавая раз- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ak − 2 |
|
|
|
|
|
личные значения k, найдем |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = |
0, a |
3 |
= |
0 |
|
и, вообще, a |
2m+ |
1 |
= 0 |
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a2 = − |
|
1 |
|
|
, |
a4 |
= |
|
|
|
|
1 |
|
, Κ |
, |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2(2n |
+ |
2) |
2 4(2n |
+ |
|
2)(2n + 4) |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
a2m |
= (− 1)m |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
,Κ |
m = (1,2...) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 4 6 Κ |
2m(2n + |
2)(2n + |
4)Κ (2n + |
2m) |
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
Подставим найденные коэффициенты в решение уравнения y = |
xr ∑∞ |
ak xk , |
|||||||||||||
получим частное решение |
|
|
|
|
|
|
k = 0 |
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
n |
|
x2 |
|
|
x 4 |
|
|
|
x6 |
|
|
|
|
|
y1 = x |
1 |
− |
|
+ |
|
|
|
− |
|
|
|
|
+ Κ |
. |
|
2(2n + 2) |
2 |
4(2n + 2)(2n + |
4) |
2 |
4 6(2n + 2)(2n + 4)(2n + 6) |
||||||||||
|
|
|
|
|
|
|
|||||||||
Решение y1 , умноженное на некоторую постоянную a0 = |
1 |
, называ- |
|||||||||||||
2n Г (n + 1) |
|||||||||||||||
ется функцией Бесселя первого рода n-го порядка и обозначается символом J n (x) .
Решение y2 , соответствующее значению r = -n, обозначают символом J − n (x) и находят по формулам
|
− n |
|
x2 |
|
|
x4 |
|
|
|
x6 |
|
|
|
|
|
y2 = x |
1 |
− |
|
|
+ |
|
|
− |
|
|
|
|
+ Κ |
. |
|
2(− 2n + |
2) |
2 4(− 2n + 2)(− 2n + |
4) |
2 4 6(− 2n + |
2)(− 2n + |
4)(− 2n + |
6) |
||||||||
|
|
|
|
|
|
|
Таким образом, при n , не равном целому числу, общее решение уравнения (23) имеет вид: y = C1 J n (x) + C2 J − n (x) .
В выборе a0 участвует гамма-функция Γ(n + 1) , которая определяется несобственным интегралом
|
|
|
Γ(n) = |
∞∫e− |
x xn− 1dx (n > 0) |
|
|
(Г(n+1)=nГ(n)), |
|||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Γ |
1 |
= π , |
Γ 3 |
|
= 1 |
π , |
Γ 5 |
|
= |
3 |
π |
, Γ |
7 |
= 15 π ,Κ . |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
8 |
|
|
|
2 |
|
|
2 |
|
|
|
|
2 |
||||
31
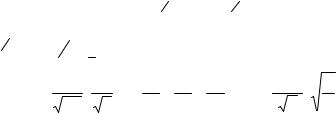
2. Если n ≥ 0 есть целое число, то первое решение y1 будет иметь
смысл и являться первым частным решением уравнения (23), но второе решение не будет иметь смысла, так как один из множителей знаменателя в разложении обратится в нуль.
При целом положительном n |
функция Бесселя имеет вид |
J |
|
(x) = |
|
1 |
|
y |
|||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
(а при n = |
0 , |
y1 |
умножается на 1), т. е. |
|
|
|
|
|
|
|
n |
|
2n n! |
1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
J n |
(x) = |
x n |
|
|
x2 |
|
|
|
x |
4 |
|
|
|
|
|
x6 |
|
|
|
|
+ Κ |
|
|
||||
|
|
|
1 − |
|
|
+ |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|||||
2 |
n |
|
|
2(2n + 2) |
|
2 4(2n + 2)(2n + 4) |
2 |
|
4 6(2n + 2)(2n + |
4)(2n + 6) |
|
||||||||||||||||
или |
|
|
n! |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n+ 2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
(− 1)m |
|
|
x |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
J n (x) = |
∑ |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m!(n + m)! |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
m= 0 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
Можно показать, что второе частное решение в этом случае нужно ис-
кать в форме K n (x) = J n (x) ln x + x− n ∑∞ |
bk x k . |
k = 0 |
|
Подставляя это выражение в уравнение (23), мы определим коэффициенты bk . Функция K n (x) с определенными таким образом коэффициентами ум-
ноженная на некоторое постоянное, называется функцией Бесселя второго рода n-го порядка. Это и есть решение уравнения (23), образующее с первым линейно независимую систему.
Общее решение будет иметь вид: Y=C1In(x)+C2Kn(x).
Отметим, что Lim Kn(x)=∞ следовательно, если мы хотим рассматривать
x→ ∞
конечные решения при n = 0, то в общем решение нужно положить C2=0.
|
Пример1. |
Найти функцию Бесселя при n=0 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n+ 2m |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
(− |
1)m |
|
|
|
|
x |
∞ |
(− 1)m x2m |
|||||||||||||||||||
|
|
|
|
In (x) = ∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
∑ |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
m |
|
(m!) |
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
m= 0 m!(n + m) |
2 |
|
|
|
m= 0 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
I |
|
(x) = 1− |
|
x2 |
+ |
|
|
|
|
x4 |
|
|
|
|
− |
|
|
x6 |
|
|
|
+ . |
||||||||||||||||
|
|
|
0 |
4 |
|
42 (1 2)2 |
|
43 (1 2 |
3)2 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Пример 2. |
Решить уравнение x2 y'' |
+ xy' + |
(x2 − |
|
1 |
) y = 0 . |
||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
||
|
Решение: Так как n = |
|
, то общее решение уравнения имеет вид: |
||||||||||||||||||||||||||||||||||||||
|
2 |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y = C1I 12 (x) + C2 I− 12 (x) , |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
где |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
x |
4 |
|
|
|
|
|
|
x |
6 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
I 12 |
(x) = |
|
|
|
|
|
|
x |
2 |
[1− |
|
|
|
+ |
|
|
− |
|
+ ...] = |
||||||||||||||||||||||
2 |
12 Γ(3 ) |
|
2 3 |
2 3 4 5 |
2 4 6 3 5 7 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
2 |
1 |
|
(x − |
x3 + |
|
x5 |
|
− |
x7 + ...) = |
sin x |
|
2 . |
|||||||||||||||||||||||
|
|
|
|
|
|
2π |
|
|
x |
|
|
|
|
|
|
3! |
|
5! |
|
|
|
|
7! |
|
|
|
|
x |
|
π |
|||||||||||
32
