
- •§ 4. Линейные дифференциальные уравнения высших порядков
- •§ 5. Линейные однородные уравнения
- •§ 6. Линейное однородное уравнение с постоянными коэффициентами
- •§ 7. Линейные неоднородные уравнения
- •§ 10. Интегрирование дифференциальных уравнений с помощью рядов
- •§ 12. Краевые задачи в линейных дифференциальных уравнениях
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Литература

Т.В. Труфанова, А.Е. Ситун
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ В ПРИМЕРАХ И ЗАДАЧАХ
Часть II. Уравнения n-го порядка
Министерство образования Российской Федерации
АМУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Факультет математики и информатики
Т.В. Труфанова, А.Е. Ситун
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ В ПРИМЕРАХ И ЗАДАЧАХ
Часть II. Уравнения n-го порядка
Благовещенск
ББК 22.161.6я73 |
Печатается по решению |
Т80 |
редакционно-издательского совета |
|
факультета математики и информатики |
|
Амурского государственного |
|
университета |
Т.В. Труфанова, А.Е. Ситун
Дифференциальные уравнения в примерах и задачах. Часть II. Уравнения n-го порядка. Учебно-методическое пособие. Благовещенск:
Амурский гос. ун-т, 2001.
Пособие содержит краткие теоретические сведения по общему курсу «Дифференциальные уравнения». Подробно рассматриваются методы решения основных типов дифференциальных уравнений n-го порядка. Студентам предлагаются варианты самостоятельной работы по данной теме. Материал пособия позволяет выработать практические навыки в решении и исследовании дифференциальных уравнений.
Пособие предназначено для студентов специальностей 010100 – математика, 010200 – прикладная математика, 010400 – физика.
Рецензент: А.И. Родионов, доцент кафедры ТМ и СМ НГТУ, канд. физ.-мат. наук.
Амурский государственный университет, 2001
§1. ОБЩИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Дифференциальное уравнение n-го порядка имеет вид
F (x, y, y', y'',..., y(n) )= 0 , |
(1) |
где х – независимая переменная, у – искомая функция, а функция F определена и непрерывна в некоторой области G R n+ 2 (n ≥ 1) .
Дифференциальное уравнение n-го порядка, разрешенное относительно старшей производной, имеет вид
y(x0 ) = y0 , y'(x0 ) = y'0 ,…, y(n− 1) (x0 ) = y0 |
(n− 1) , |
(3) |
|
где x0 (a,b) , y0 , y'0 ,…, y0 |
(n− 1) – заданные числа. |
|
|
Теорема Пеано. Если функция f непрерывна в области D, то для любой точки (x0 , y0 , y'0 ,...y0 (n− 1) ) D существует решение уравнения (2), определенное в некоторой окрестности точки x0 (a, b) и удовлетворяющее условиям (3).
Существование и единственность решения задачи Коши определяется следующей теоремой.
3
Теорема Коши – Пикара. Если функция f непрерывна в области D и
имеет непрерывные частные производные |
∂ f |
, |
∂ f |
,..., |
∂ f |
, то для любой точ- |
|
∂ y' |
∂ y (n− 1) |
||||
|
∂ y |
|
|
|||
ки (x0 , y0 , y'0 ,...y0 (n− 1) ) D существует единственное решение уравнение (2), определенное в некоторой окрестности точки x0 (a, b) и удовлетворяющее условиям (3).
Общим решением уравнения (1) или (2) называется такая функция y = ϕ (x, c1,..., cn) , которая при любых допустимых значениях параметров
c1 , c2 ,..., cn является решением этого дифференциального уравнения и для любой задачи Коши с условиями (3) найдутся постоянные c1 , c2 ,..., cn , определяемые из системы уравнений:
|
y0 = |
ϕ |
(x0c1,c2 ,...,cn ) |
|
||
|
y'0 = |
ϕ |
'(x0 c1,c2 ,...,cn ) |
|
||
.... |
|
|
|
|
|
|
|
(n− 1) |
|
(n− 1) |
(x0 c1,c2 ,...,cn ) . |
|
|
|
= ϕ |
|
||||
|
y0 |
|
|
|
||
Уравнение |
|
|
|
|
|
|
|
Φ (x, y,c1,c2 ,...,cn ) = 0 , |
(4) |
||||
определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения.
Частным решением уравнения (1) или (2) называется любое решение, получаемое из общего решения при конкретных числовых значе-
ниях c1,c2 ,...,cn .
Если y(x) – решение уравнения (1), то график функции y = y(x) называется интегральной кривой уравнения (1).
Геометрически общее решение (общий интеграл) представляет собой семейство интегральных кривых на плоскости, зависящие от n параметров
c1,c2 ,...,cn .
Функция φ (x) называется особым решением дифференциального уравнения (1), если:
1) φ (x) обращает дифференциальное уравнение (1) в тождество;
2) для любой |
точки |
x0 (a, b) задача Коши с начальными условиями |
y(x0 ) = φ ( x0) , y(' |
x)0 = φ(' |
x)0 ,..., y(n− 1) (x0 ) = φ (n− 1) (x0 ) имеет более одного решения. |
4

§ 2. УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ, РАЗРЕШАЕМЫЕ В КВАДРАТУРАХ
2.1 Уравнение вида |
|
F (x, y(n) ) = 0 , |
(5) |
которое содержит только производную n-го порядка искомой функции и независимую переменную.
|
Запишем уравнение (5) в параметрической форме |
x = ϕ |
|
(t) , |
|
y(n) |
= φ (t) , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
где |
ϕ (t) – дифференцируемая функция. Общий интеграл уравнения (5) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
найдется в параметрической форме. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Имеем dy (n− 1) = |
y( n) |
dx , dy(n− 1) |
= φ (t) ϕ '(t)dt , откуда y(n− 1) = |
∫ϕ |
′(t) φ |
(t) dt + c1 |
= |
φ 1( t,c1) . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Аналогично находим y (n− |
2) |
|
|
и т.д. Система |
x = |
ϕ |
(t) |
|
|
|
|
|
|
|
|
|
|
|
является |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
общим интегралом уравнения (5). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
φ |
n (t, c1 , c2 ,..., cn ) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
Пример 1. Найти общее решение уравнения y' ' ' = |
|
|
1 − |
x 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Решение. |
Введем |
параметр |
t, |
|
|
|
|
положив |
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
π |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x = |
sin t t |
|
− |
|
|
|
, |
|
|
|
|
, |
тогда |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
y' ' ' = |
|
cos t |
|
= cos t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Данное уравнение в параметрической форме имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
|
sin t, |
y'''= cost . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Проинтегрируем полученное выражение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
tdt , y' ' = |
|
∫ cos |
2 |
|
|
|
|
|
|
|
|
|
c1 |
|
, y' ' = |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|||||||||||||||||||
|
|
|
|
dy' ' = |
y' ' ' dx = cos |
|
|
|
|
|
tdt + |
|
|
|
|
|
|
|
|
|
t |
+ |
|
|
|
sin 2t + |
|
c1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
∫ |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
dy' = y' ' dx = |
|
|
|
t |
+ |
|
|
|
|
sin 2t |
+ |
|
c1 cos tdt , |
y' = |
|
|
|
|
t cos t |
+ |
|
|
sin 2t cos t + |
c1 |
cos t dt + |
|
|
, |
|||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
2 |
|
|
|
2 |
2 |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y' = |
|
|
|
t sin t + |
cos t − |
|
|
|
|
cos |
|
|
|
t |
+ |
|
c1 |
sin t + |
c2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
dy = |
|
|
y' dx = |
|
|
|
t sin t + |
cos t − |
|
|
|
|
|
cos |
|
|
t |
+ |
|
c1 |
|
|
sin t + c2 |
|
cos tdt , |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c3 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
||||||||||||||||
|
|
|
|
y = |
|
|
|
|
|
|
t sin 2t + |
cos |
|
t |
− |
|
|
cos |
|
|
|
t |
+ |
|
|
|
|
c1 |
sin 2t + c2 |
cos t dt + |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
2 |
|
3 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
3 |
|
|
7 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
y = |
|
|
|
− |
|
|
|
t cos 2t |
+ |
|
|
t + |
|
|
|
|
sin 2t − |
|
|
|
|
|
sin 4t − |
|
|
|
|
c1 cos 2t + c2 sin t + |
|
c3 |
. |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
8 |
24 |
|
|
96 |
4 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
5

Общее решение в параметрической форме записывается
|
|
|
|
|
|
|
π |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x = |
sin t t |
|
− |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
3 |
|
|
7 |
|
1 |
|
c1 |
|
c2 |
|
c3 |
|
|||||
|
y = |
− |
t cos 2t + |
|
|
t + |
sin 2t − |
sin 4t − |
cos 2t + |
sin t + |
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
8 |
16 |
48 |
192 |
8 |
2 |
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
где C1,C2,C3 – произвольные постоянные.
Пример 2. Найти частное решение уравнения y' '2 − x 2 = 1, y(0)=0,
y’(0)=1.
Решение. Решим задачу Коши. Для этого найдем общее решение заданного уравнения и, учитывая начальные условия, получим частное ре-
шение |
уравнения. Введем параметр t, положив x = sh t, t R . Тогда |
||||
y' '2 = 1 + |
sh2 t = ch2 t , |
|
y' ' |
|
= cht . |
|
|
||||
Запишем заданное уравнение в параметрической форме:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
sh t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y''= |
ch t, |
||
имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
ch 2 tdt , |
|
|
∫ ch 2 tdt + |
c1 , |
|||||||||||||||
dy'= |
y''dx = |
|
y'= |
|||||||||||||||||||||||
y'= |
1 |
|
|
∫ (1+ ch 2t)dt + |
|
c1 |
= |
1 |
t + |
1 |
sh 2t + c1 , |
|||||||||||||||
2 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
, |
|||
dy = y'dx = |
|
|
t + |
|
|
|
sh 2t + |
c1 |
ch t dt |
|||||||||||||||||
2 |
4 |
|
||||||||||||||||||||||||
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y = ∫ |
|
|
t ch t + |
|
|
|
sh 2t ch t + |
|
c1 ch t dt + c2 , |
|||||||||||||||||
2 |
4 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
y = |
|
1 |
t. sh t − |
|
1 |
ch t + |
|
1 |
ch3 |
t + c1 sh t + c2 . |
||||||||||||||||
|
2 |
2 |
6 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Запишем общее решение уравнения в параметрической форме:
|
x = |
sh t |
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
y = |
t |
. |
sh t − |
ch t + |
ch |
3 |
t + c1 sh t + c2 . |
||||
|
|
|
|
|
|
|
||||||
2 |
|
2 |
6 |
|
||||||||
|
|
|
|
|
|
|
|
|
||||
Учитывая начальные условия, найдем C1 и C2. Если x=0, то sh t=0 или 12 (et − e− t ) = 0 , откуда t0 = 0 . Подставляя в решение t=0, y(0)=0, y’(0)=1, по-
лучим c1 = 1, c2 = 13 . Запишем частное решение уравнения в параметрической форме:
|
x = |
sh t |
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
y = |
t |
. |
sh t − |
ch t + |
ch |
3 |
t + sh t + |
. |
|||||
|
|
|
|
|
|
|
|
|||||||
2 |
|
2 |
6 |
|
3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||
6
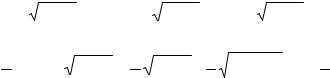
Выразим t через x. Имеем |
|
1 |
(et |
− e− t ) |
= x , e2t |
− 2xet − |
1 = |
0 , откуда |
|||||||||||||||||
2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
et = x + |
x 2 + 1 , t = ln(x + |
x 2 + 1), ch t = |
x2 + 1 . |
|
|
|
|||||||||||||||||||
Частное решение уравнения записывается |
|
|
|
|
|
|
|
||||||||||||||||||
y = 1 x ln(x + |
x 2 + 1)− 1 |
x 2 + |
1 + 1 |
(x 2 + 1)3 + |
x + |
1 . |
|
||||||||||||||||||
|
2 |
|
|
|
|
2 |
|
|
|
|
6 |
|
|
|
|
|
3 |
|
|
||||||
2.2. Уравнения вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
y (n) = |
f (x) |
|
|
|
|
|
|
|
(6) |
||||||
Данное уравнение |
рассматривается как частный случай уравнения (5), |
||||||||||||||||||||||||
где f(x) непрерывная функция на (a,b). |
|
|
|
|
|
|
|
|
|||||||||||||||||
Если принять x = |
x |
(a, b) в качестве параметра, то общее решение уравне- |
|||||||||||||||||||||||
ния (6) получим в форме: y = |
∫ ∫...∫ f (x)dxdx...dx + |
c1xn− 1 + |
c2 xn− 2 + |
... + cn− 1x + cn |
|||||||||||||||||||||
Общее решение уравнения (6) в форме Коши имеет вид: |
|
||||||||||||||||||||||||
y = ∫x ∫x ...∫x |
f (x)dxdx...dx + |
|
y0 |
(n− 1) |
(x − |
x0 ) n− 1 + |
y0 |
(n− 2) |
|
(x − |
x0 ) n− |
2 + ... + |
y0 '(x − x0 ) + y0 , |
||||||||||||
|
(n − 1)! |
(n − 2)! |
|||||||||||||||||||||||
x0 x0 x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где x0 (a, b), y0 , y0 ',..., y0 |
(n− 1) |
- любые числа. |
|
|
|
|
|
|
|
||||||||||||||||
Пример 3. Найти общее решение уравнения |
y' ' = |
1 |
. |
||||||||||||||||||||||
cos 2 x |
|||||||||||||||||||||||||
Решение. Интегрируя первый раз, получим |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y'= |
tg x + |
c1 . |
|
|
|
|
|
|||||||
Повторное интегрирование приводит к общему решению |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y = |
− |
ln |
|
cos x |
|
+ |
c1 x + c2 . |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2.3. Уравнения вида
F (y (n− 1) , y( n) ) = 0
Если данное уравнение разрешимо относительно y (n) , т.е. y (n) =
то, вводя новую функцию u = |
y (n− 1) , приведем уравнение к виду |
|
|||
Общий интеграл полученного уравнения имеет вид: |
x + c1 = ∫ |
du |
( |
||
f (u) |
|
||||
или |
∫ ∫ ...∫ φ (x,c1)dxdx...dx + |
|
|
|
|
u = φ (x, c1) , y (n− 1) = φ (x, c1) , y = |
c2 xn− 2 + ... + cn− 1x + |
||||
(7)
f (y( n− 1) ) , u'= f (u) .
f (u) ≠ 0)
cn .
n - 1
7
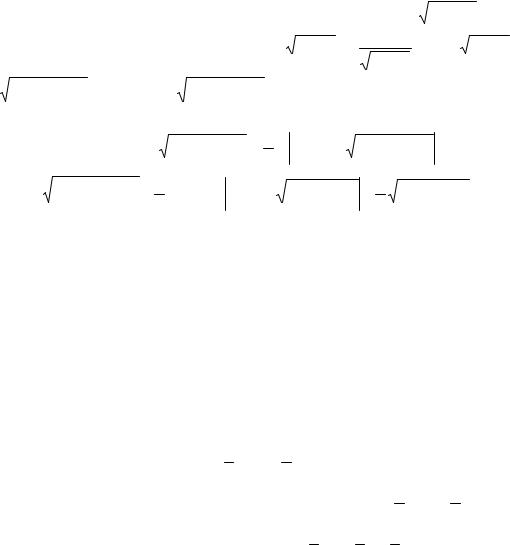
Если уравнение |
(7) |
|
имеет |
|
параметрическое |
|
представление |
|
y (n) |
= ϕ |
(t) , |
||||||||||||||||||||||
y (n− 1) = φ (t) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n− 1) |
|
φ '(t) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
n− 1 |
|
|
n |
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|||||
то |
|
|
|
|
dy ( |
) |
= y |
|
dx |
, dx = |
|
|
|
|
= |
|
|
|
dt , |
|
|
|
|
|
|
|
|
||||||
|
φ ' (t) |
|
|
|
|
y(n) |
|
ϕ (t) |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
ξ(t, c1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
откуда x = |
∫ |
|
dt + |
c1 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ϕ (t) |
|
|
|
|
|
|
|
|
|
(t)φ '( t) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n− |
2 |
|
|
φ |
|
|
|
|
|
|
|
|
|
|
||||
|
n− |
2 |
|
n− 1 |
|
φ (t)φ |
'( t) |
|
|
|
|
( |
|
) |
|
∫ |
|
|
|
|
|
|
|
n− |
3 |
|
n− |
2 |
|
|
|||
|
|
|
|
|
|
y |
|
= |
|
|
|
|
dt + c2 , |
|
|
|
|
||||||||||||||||
Далее dy( |
|
) = y( |
) dx = |
|
|
|
|
dt , |
|
|
|
|
|
ϕ (t) |
dy( |
|
) = y( |
|
) dx , |
|
|||||||||||||
|
|
ϕ (t) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
dy = |
|
|
|
|
∫ y' dx + |
|
|
η (t, c2 , c3,..., cn) . |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
y'dx , |
|
y = |
cn = |
|
|
|
|
|
|
|
|||||||||||||||||||
Общий интеграл уравнения (7) записывается в параметрической форме: |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
= ξ(t,c1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
= η (t,c2 ,c3 ,...,cn ) . |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Пример 4. Найти общее решение уравнения y' ' ' y' ' = |
1 + |
y' '2 . |
|
|
|
|
|
||||||||||||||||||||||||||
Решение. Пусть |
y' ' = |
u , |
тогда u' u = |
1 + |
u 2 , |
|
udu |
= dx , |
1 + |
u 2 |
= |
x + |
c1 , |
||||||||||||||||||||
u = ± (x + c1) 2 − 1, или y' ' = |
± (x + |
c1) 2 − 1 . |
|
|
|
|
|
|
1 + u 2 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Последовательным интегрированием находим |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
y' = ± |
|
1 |
(x + c1) ( |
x + c1) |
2 |
− 1 |
− |
1 |
ln x |
+ c1 + |
|
(x + c1) |
2 |
− |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
2 |
|
2 |
|
|
||||||||||||||||||||||||||||
|
|
1 |
(( |
|
|
|
|
) |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
+ 1) |
2 |
− |
3 |
− |
( |
|
+ 1) |
|
|
|
+ |
|
1 |
+ |
( |
|
+ |
1) |
2 |
− |
|
+ |
( |
|
+ |
||||||||
|
= ± |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
y |
|
6 |
|
x |
c |
|
|
|
|
1 |
|
|
2 |
|
x |
c |
ln x |
|
c |
|
|
x |
|
c |
|
|
1 |
|
2 |
|
x |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Знак плюс соответствует общему решению для области
– для области y' ' <0 .
1 |
|
+ |
|
c2 , |
|
|
|
|
|||
|
|
|
|
|
|
c1) |
2 |
− |
+ c2 x + c3 . |
||
|
1 |
||||
|
|
|
|
|
|
y' ' >0 , знак минус
|
Пример 5. Найти решение задачи Коши y' '− 2 y' = |
1, |
y(0) = |
5 |
|
, |
y'(0) = 1. |
||||||||||||
|
4 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Решение. Пусть y' = |
u , тогда u'− 2u = 1, |
|
|
du |
|
= |
dx , |
|
|
1 |
ln |
|
1 + 2u |
|
= x , |
|||
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
+ 2u |
|
|
2 |
|
c |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
u = |
c1e2 x − |
1 |
или y' = c1e2 x − |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Интегрируя полученное уравнение, находим общее решение:
y = 12 c1e2 x − 12 x + c2 .
Учитывая начальные условия, определим c1 и c2 : c1 = 32 , c2 = 12 .
Частное решение уравнения запишется y = 34 e2 x − 12 x + 12 .
8
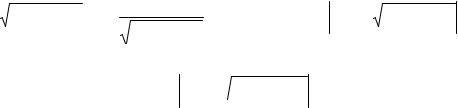
2.4. Уравнения вида
F (y (n− 2) , y( n) ) = 0 |
(8) |
С помощью замены y (n− 2) = u уравнение (8) приводится к уравнению второго порядка F (u, u' ' ) = 0 .
Если полученное уравнение разрешимо относительно функции u", то, учитывая замену, получаем промежуточный интеграл вида:
φ (x, y (n− 2) , c1 , c2 ) = 0 ,
т.е. дифференциальное уравнение (n-2) порядка, которое интегрируется в квадратурах.
Пример 6. Понизить порядок уравнения до первого порядка (решать уравнение не требуется) y' ' '− y' = 1.
Решение. С помощью замены y' = u приведем данное уравнение к уравнению второго порядка u' '− u = 1, u' ' = 1 + u .
Умножая на интегрирующий множитель = |
2u' , приходим к уравнению |
|||
|
2u'u''= 2(1+ u)u' . |
|||
Интегрируя, получим первый интеграл уравнения |
||||
u'2 = |
2(1+ u) 2 |
|
+ c1 , u'2 = (1+ u) 2 + c1 . |
|
2 |
|
|||
|
|
|
|
|
Откуда находим общий интеграл вспомогательного уравнения |
||||
u'= ± (1+ u) 2 + c1 , ± |
du |
|
= dx , |
x + c2 = ln1+ u + (1+ u) 2 + c1 . |
|
(1+ u) 2 |
+ c1 |
|
|
Возвращаясь от переменной u к y' , получим уравнение первого порядка
x + c2 = ln1+ y'+  (1+ y') 2 + c1 .
(1+ y') 2 + c1 .
§3. УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА
Ниже приводятся некоторые виды |
дифференциальных |
уравнений |
n-го порядка, допускающие понижение порядка. |
|
|
3.1. Уравнения вида |
|
|
F( x, y(k ) ,..., y(n) ) = |
0 , |
(9) |
т.е. уравнения, не содержащие явно искомой функции и ее производных до порядка k-1 включительно.
9

С помощью замены y(k) = p(x) , где p(x) , новая неизвестная функция, порядок уравнения понижается на k единиц: F (x, p, p',..., p(n− k ) ) = 0 . Предположим, что для полученного уравнения мы можем найти общее решение p( x) = ϕ ( x,c1,c2 ,...,cn− k ) .
Следовательно имеем промежуточный интеграл y(k ) = ϕ (x,c1,c2 ,...,cn− k ) .
Общее решение уравнения (9) получается путем k-кратного интегрирования обеих частей полученного выражения.
Пример 1. Найти частное решение уравнения
x4 y'''+ 2x3 y'' = 1, y(1) = 12 , y'(1) = 12 , y''(1) = − 1.
Решение. Данное уравнение не содержит y и y’. Положим y''= p(x) ,
тогда y''' = |
dp |
|
и уравнение имеет вид |
x4 |
dp |
+ |
|
2x3 p = 1 или |
|
dp |
+ |
|
|
2 |
|
p = |
|
1 |
|
. |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
dx |
|
x |
|
|
|
x4 |
|
|
|||||||||||||||
Это линейное |
уравнение |
первого |
|
порядка, |
которое |
|
решается заменой |
|||||||||||||||||||||||||||||||||||||||||||||
p(x) = u(x)v(x), |
p' = |
u' v + uv' . Производя замену получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
, |
|
|
|
|
|
|
|
|
2u |
|
|
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
u'v + uv'+ |
|
|
|
uv |
= |
|
|
|
|
|
|
|
v |
u'+ |
|
|
|
+ v'u = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
x |
x |
4 |
|
|
|
|
|
x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
откуда, с учетом возможности произвольного выбора функции u(x), |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
du |
+ |
|
2u |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
dv |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
u = |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решая первое уравнение системы, |
|
найдем функцию |
|
u = |
|
1 |
|
|
, из второго |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
x2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c1 |
|
||||
уравнения – функцию v = − |
1 |
+ c1 . Найдем функцию p = |
|
uv , |
|
|
|
|
p = |
− |
1 |
+ |
. |
|||||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 1, получим c1 = |
|
|
|
|
|
|
x3 |
x 2 |
|||||||||||||||||||
Используя начальное условие |
y''(1) = p(1) = |
0 . |
Следова- |
|||||||||||||||||||||||||||||||||||||||||||||||||
тельно, y'' = |
− |
1 |
, откуда y' = |
|
|
|
1 |
+ |
|
c |
2 |
|
. Начальное условие y'(1) = |
|
1 |
|
|
позволяет |
||||||||||||||||||||||||||||||||||
x3 |
|
|
2x2 |
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
найти c2 = |
0 . Следовательно, |
y' = |
|
|
|
|
1 |
, |
|
|
|
y |
= − |
1 |
+ c3 . Из условия y(1) = 1 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
следует, что c3 = 1. |
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Итак, искомое частное решение есть |
y = |
1− |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
10
3.2. Уравнения вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F ( y, y',..., y(n ) ) = 0 |
|
|
|
|
|
|
|
|
(10) |
|||||||
Уравнение (10) явно не содержит независимую переменную. |
||||||||||||||||
Подстановкой y' = p( y) , y''= p |
dp |
, |
|
|
dp |
2 |
2 |
d 2 p |
|
2 |
|
2 |
|
и т.д. по- |
||
|
y'''= |
p |
|
|
+ p |
|
|
|
= |
pp' |
+ p |
|
p'' |
|||
|
|
|
|
2 |
|
|||||||||||
|
dy |
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|||
рядок уравнения понижается на единицу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пример 2. Найти общее решение уравнения y' y'''− |
3y''2 = 0 . |
|||||||||||||||||||||||||
Решение. Пусть y' = |
p( y) , |
|
|
|
|
dp |
, |
|
|
|
dp |
2 |
|
|
2 d 2 p |
. Тогда уравне- |
||||||||||
y'' = |
p |
|
|
y'' = |
p |
|
|
|
|
|
+ |
p |
|
|
|
|
||||||||||
dy |
|
|
|
|
|
dy |
2 |
|||||||||||||||||||
|
|
|
|
|
2 |
|
2 |
|
|
|
dy |
|
|
2 |
|
|
|
|
||||||||
|
|
dp |
|
|
|
|
|
|
|
dp |
|
|
|
|
|
|||||||||||
ние преобразуется к виду |
|
|
|
|
|
d p |
|
|
|
|
0 . |
|
|
|||||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|||||||||||||||
p |
p |
|
|
|
+ |
p |
|
|
|
|
− 3p |
|
|
|
|
= |
|
|
||||||||
dy |
|
|
dy2 |
|
dy |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Приведя подобные члены и сократив на |
p2 |
(при этом следует учесть те- |
||||||||||||||||||||||||||||||||||||||||||||
ряемое решение p=0, или y=c), получим: |
|
d 2 p |
|
dp |
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||
p |
|
|
|
− 2 |
|
|
= 0 , pp''− |
2 p' |
|
|
|
= |
0 . |
|
|
|||||||||||||||||||||||||||||||
dy |
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
dp |
|
|
d 2 p |
|
dz |
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Положив здесь |
|
= z , |
|
= z |
, приводим уравнение к виду: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
dy2 |
dp |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pz |
− |
2z2 = |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dp |
|
|
|
|
|
|
|
|||||
Сократив на z (при этом следует учесть еще одно решение z = |
|
|
= |
0 |
, т.е. |
|||||||||||||||||||||||||||||||||||||||||
|
dy |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
2dp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
p = |
c1 |
и |
y = |
c1 x + c2 ), |
получим |
|
− |
= |
0 , |
откуда |
ln |
|
z |
|
− ln p2 = ln |
|
c1 |
|
, |
или |
||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
dp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
z = |
= |
− |
c p2 . |
|
Интегрируя |
последнее уравнение, |
находим: − |
|
= |
|
|
− c y − c |
2 |
, |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
dy |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
или |
dx |
= |
c y + |
c |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
dy |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Общий интеграл уравнения запишется x = |
c1 y 2 + |
c2 y + c3 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Вобщее решение входят потерянные ранее частные решения.
3.3.Уравнения вида
d |
F (x, y, y',..., y(n− 1) ) = |
0 , |
(11) |
|
dx |
||||
|
|
|
т.е. уравнения, в которых левая часть может быть представлена как полная производная по x от некоторой функции F (x, y, y',..., y(n− 1) ) .
11

Интегрируя по x, получим новое уравнение, порядок которого на единицу ниже порядка исходного уравнения. Такие уравнения называются уравнениями в точных производных.
Пример 3. Найти общее решение уравнения
(1+ x2 )y''+ 2xy' = x3 .
Решение. Левая часть уравнения есть полная производная по x от
функции (1+ x2 )y' , а правая – от функции |
|
x4 |
, т.е. уравнение можно перепи- |
|||||||||||||||||||
4 |
||||||||||||||||||||||
сать так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
x4 |
′ |
|
|
|
|
|
|
|
|
|||||
|
|
|
((1+ |
2 |
) y′)′= |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x |
|
4 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
c |
x4 + |
c |
|||||
Отсюда интегрированием получаем (1+ |
|
x2 )y' = |
||||||||||||||||||||
|
|
+ |
1 |
или dy = |
4(1+ |
x21) |
dx . |
|||||||||||||||
|
4 |
4 |
||||||||||||||||||||
Следовательно, y = |
1 |
x3 − |
|
1 |
x + |
c1 |
arctg x |
+ |
c2 |
есть общее решение уравнения. |
||||||||||||
|
4 |
4 |
||||||||||||||||||||
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3.4. Уравнения вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
F(x, y, y',..., y(n) ) = |
0 |
|
|
|
|
(12) |
|||||||||||||
Однородные относительно функции и ее производных, т.е. такие, что
F(x,λ y,λ y',...,λ y(n) ) = λ mF(x, y, y',..., y(n) ) , λ >0 однородности порядка m.
Подстановкой y' = yz порядок уравнения понижается на единицу, где z = z(x) – новая неизвестная функция.
Пример 4. Найти общее решение уравнения xyy''− xy'2 − yy' = 0 .
Решение. Проверим однородность уравнения. Пусть
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (x, y, y', y'') |
= xyy''− |
xy'2 − |
yy' , |
|
|
||||||
|
|
|
|
|
|
|
|
|
F(x,λ y,λ y',λ y'') = |
|
xλ yλ y''− x(λ y')2 − λ yλ y'= |
λ 2( xyy''− |
xy'− yy)' |
= |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= λ 2 F (x, y, y', y'') , |
m=2. |
|
|
||||||||
Положим y' = |
|
yz , |
тогда y'' = (yz)' = y' z + z' y = |
yz2 + |
yz' , или y'' = |
y(z2 + |
z'), и урав- |
|||||||||||||||||||
нение запишется xy2 (z2 + z')− |
xy 2 z2 − y 2 z2 |
= 0 . |
|
|
|
|
|
|||||||||||||||||||
Сокращая на |
|
y 2 |
(при этом теряется решение y=0), находим xz'− z = 0 или |
|||||||||||||||||||||||
|
dz |
− |
dx |
= 0 , z = |
|
c1x . Так как z = |
|
y' |
, то y' = |
c1 xy , |
dy |
= c1 xdx . |
|
|
||||||||||||
|
|
|
|
y |
|
|
||||||||||||||||||||
|
z |
x |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
c1 x2 |
|
|
|
|
|
|
y = c2 e c1 |
x 2 |
|
|
|
|
|
|
||
Откуда ln |
|
y |
|
= |
|
+ ln |
|
c2 |
|
или |
|
2 |
|
– общее решение уравнения (со- |
||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
держит потерянное частное решение y=0, если c2 = |
0 ). |
|
|
|||||||||||||||||||||||
12
3.5. Уравнения вида |
|
F(x, y, y',..., y(n) ) = 0 |
(12-А) |
обобщенно – однородное, если существуют числа k и m такие, что:
F (λ x,λ k y,λ k − 1 y',...,λ k − n y(n) ) = λ m F (x, y, y',..., y(n) ) .
С помощью замены x = et , y = zekt (при х>0, а при x<0 полагаем x = − et ), где t – новая независимая переменная, z = z(t) – новая искомая функция.
Уравнение (12-А) приводится к уравнению, не содержащему независимой переменной t и, следовательно, допускающему понижение порядка на единицу.
Производные при замене преобразуются по формулам:
y' = |
dy |
e |
− t |
= |
|
dz |
e |
kt |
+ kze |
kt |
|
− t |
= |
(z '+ kz)e( |
k − 1 t |
, |
||||||
dt |
|
|
dt |
|
e |
|
|
) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
dy ' |
|
|
|
|
d |
2 z |
|
|
|
dz |
|
|
|
|
|
|
|
|
|||
y'' = |
|
|
e− t |
= |
|
|
|
|
|
+ |
(2k − 1) |
|
+ |
k(k − |
1)z e(k− 2)t |
и т.д. |
||||||
|
|
|
|
2 |
|
|
||||||||||||||||
|
|
dt |
|
|
|
|
dt |
|
|
|
|
dt |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 5. Найти общее решение уравнения x4 y''+ (xy'− y)3 = 0 .
Решение. Положим F(x, y, y', y'') = x4 y''+ ( xy'− |
y) 3 . |
Имеем |
|
F (λ x,λ k y,λ k − 1 y',λ k − 2 y'') = λ 4λ k − 2 x4 y''+ (λ xλ k − 1 y'− λ k y)3 = |
λ k + 2 x4 y''+ λ 3k (xy'− y)3 = |
= λ 3 F (x, y, y', y'') (k=1), |
|
откуда следует, что данное уравнение является обобщенно – однородным
(m=3, k=1 ).
Выполним замену x = |
et , |
|
y = |
zet . Тогда |
|
|
|||||||||
Отсюда |
|
|
|
|
y' = z'+ z , y'' = (z''+ z)e− t . |
|
|||||||||
|
|
|
|
|
[et( z'+ z) − zet ]3 = 0 , z''+ z'+ z'3 = 0 . |
||||||||||
e4t (z''+ z)e− t + |
|||||||||||||||
Полученное уравнение явно не содержит независимой переменной t. |
|||||||||||||||
Пусть z' = p(z) , ( z'' = p |
dp |
). Тогда |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
dz |
|
|
|
|
|
|
|
|
|
dp |
|
|
|
|
dp |
+ |
p + |
|
3 |
= |
|
|
|
|
2 |
|
|||
p |
|
|
p |
|
0 , |
p |
|
|
+ 1+ p |
= 0 |
, |
||||
dz |
|
|
dz |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
откуда имеем два уравнения dp |
+ |
1+ |
p2 |
= 0 и p = |
0 . |
|
|||||||||
|
|
|
|
|
dz |
|
|
|
|
|
|
|
|
||
13

Из второго уравнения p = |
|
0 следует z' = |
0 , |
z = |
c или y = |
cx . |
|
||||||||||||||||
Из первого уравнения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dp |
= − |
dz , arctg p = |
|
c |
|
− |
z , |
p = |
tg(c − |
z) . |
|
|||||||||||
1+ p 2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
||
Поэтому |
|
|
tg(c1 − |
|
z) , ctg(c1 − |
z)dz = |
|
|
|
|
|||||||||||||
|
|
z' = |
|
|
dt , |
|
|
|
|||||||||||||||
|
|
∫ctg(c1 − |
z)dz = |
t − |
|
ln c |
(c >0) , |
|
|
|
|||||||||||||
sin(z − |
c ) |
|
ln |
|
sin(z − |
c1) |
|
= |
|
− t + |
ln c , |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
= |
|
c |
e− t |
( |
c |
2 |
≠ 0 |
|
z |
= |
c |
+ arcsin c |
e− t |
. |
|
||||||||
|
|
1 |
|
|
2 |
|
|
|
|
|
) , |
|
|
|
1 |
|
2 |
|
|
||||
Учитывая замену y = |
|
|
|
− t |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
zx , |
|
e |
|
= |
|
, находим y = |
x c1 + arcsin |
|
. |
||||||||||||||
|
|
x |
x |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если c1 = c , c2 = 0 , то имеем рассмотренное выше решение y = cx .
Замечание 1. В некоторых случаях найти решение дифференциального уравнения методом понижения порядка в виде явной или неявной функции затруднительно, однако удается получить решение в параметрической форме.
Пример 6 (к замечанию 1). Найти общее решение уравнения y' ' (1 + 2 ln y') = 1.
Решение. Пусть y' = t , y' ' = dxdt . Тогда уравнение примет вид
|
|
dt |
(1 + 2 ln t) = 1, или dx = (1 + |
2 ln t)dt , |
|
|
dx |
||
|
|
|
t(1 + 2 ln t)dt , |
|
откуда x = |
− t + 2t ln t + c1 . Так как dy = tdx , то dy = |
|||
откуда y = |
t 2 ln t + c2 . |
|
|
|
Общее решение запишется в параметрической форме:
|
x = t(− 1+ 2ln t) + c1 |
||
|
y = t |
2 |
ln t + c2 . |
|
|
||
14
§4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
Линейным дифференциальным уравнением n-го порядка называется уравнения вида
y(n) + |
a (x) y(n− 1) |
+ |
a |
2 |
(x) y(n− 2) |
+ ... + a |
n− 1 |
(x) y'+ a ( x) |
y = |
f( x) |
. |
(13) |
|
1 |
|
|
|
|
n |
|
|
Здесь функции a1 (x), a2( x) ,..., an( x) , (f )x заданы и непрерывны на интервале
(a,b) .
Если f (x) ≡ 0 , то уравнение (13) называется линейным однородным, если f (x) ≠ 0 , то уравнение (13) называется линейным неоднородным,
или линейным уравнением с правой частью.
Краткая |
запись линейного |
неоднородного |
уравнения (13) имеет вид |
L( y) = f( |
x) , где L – линейный дифференциальный оператор n-го порядка, т.е. |
||
|
L( y) = |
y (n) + a1 (x) y(n− 1) + ... + |
an (x) y , |
определенный на множестве n раз непрерывно дифференцируемых на (a, b)
функций.
Краткая запись линейного однородного уравнения соответственно имеет вид L( y) = 0 .
4.1. Решение линейных однородных и неоднородных дифференциальных уравнений n-го порядка методом понижения порядка уравнения.
Зная одно частное решение y1 (x) линейного однородного уравнения, можно с помощью замены искомой функции y(x) = y1( x) ∫ z( x) dx понизить
его порядок, а следовательно, и порядок соответствующего неоднородного уравнения (13) на единицу. Полученное уравнение (n-1)-го порядка относительно z также является линейным.
|
Пример 1. |
Дано уравнение y'''+ |
2 |
y''− y'+ |
1 |
y = |
x и известно частное |
||||||
|
|
x ln x |
|||||||||||
|
|
|
y1 = |
ln x |
|
x |
|
|
|
|
|||
решение |
соответствующего |
однородного |
|
уравнения: |
|||||||||
y'''+ |
2 |
y''− y'+ |
1 |
|
y = 0 . |
|
|
|
|
|
|
|
|
|
x ln x |
|
|
|
|
|
|
|
|
||||
|
x |
|
|
|
|
|
|
|
|
|
|||
|
Понизить порядок уравнения. |
ln x∫ zdx , где z |
|
|
|
||||||||
|
Решение. Выполним замену y = |
– новая неизвестная |
|||||||||||
функция. Тогда, |
подставляя соответствующие производные y' = |
1 |
∫ zdx + z ln x , |
||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
15
y'' = − |
1 |
∫ zdx + |
2z |
+ |
z'ln x , y''' = |
2 |
∫ zdx − |
3z |
+ |
|
3z' |
+ z''ln x |
в данное уравнение, по- |
|||||
x2 |
x |
x3 |
x2 |
|
|
x |
|
|||||||||||
лучим: |
|
|
|
|
3 |
+ 2ln x |
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
x . |
|||||||||
|
|
|
|
|
z''ln x + |
|
|
|
|
z'+ |
|
|
|
|
|
− |
ln x z = |
|
|
|
|
|
|
|
|
x |
x |
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Порядок линейного неоднородного уравнения понижен на единицу.
|
Пример 2. |
|
Найти общее |
|
|
решение |
уравнения |
y''+ |
2 |
y'+ y |
= 0 , если |
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|||||||
известно его частное решение y1 |
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Решение. Выполним замену y = |
|
|
∫ zdx , тогда |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y' = |
x cos x − sin x |
∫ zdx + |
|
|
sin x |
z |
, |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
y''= |
|
sin x |
z'+ |
|
2(xcos x − sin x) |
z − |
|
(x2 − |
2)sin x + |
2xcos x |
∫ zdx . |
|
|
|||||||||||||||||||||||
|
|
|
x |
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Имеем уравнение |
z'sin x + |
2z cos x = |
0 , |
|
|
решая которое |
|
найдем |
|
функцию |
||||||||||||||||||||||||||||
|
c1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2 x |
|
|
sin x |
|
|
c dx |
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
cos x |
|
|
||||||||||
Следовательно, |
y = |
|
∫ |
= |
(c2 − |
c1 ctg x) = c2 |
− c1 |
|
. |
|
||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
x |
|
sin |
2 x |
|
|
x |
|
x |
|
|
x |
|
|
||||||||||||||||||||||||
Общее решение уравнения: |
y = |
c2 |
sin x |
− c1 |
|
cos x |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§5. ЛИНЕЙНЫЕ ОДНОРОДНЫЕ УРАВНЕНИЯ
Линейное однородное уравнение n-го порядка имеет вид
y(n) + a1 (x) y(n− 1) + a2 (x) y(n− 2) + ... + an− 1 (x) y'+ an( x) y = 0 |
(14) |
или L( y) = 0 . |
|
Общее решение линейного однородного уравнения (14) записывается |
|
y = c1 y1 (x) + c2 y2( x) + ... + cn yn( x) , |
|
где c1 ,c2 ,...,cn – произвольные постоянные, а y1 (x), y2( x) ,..., yn( x) |
– фундамен- |
тальная система частных решений уравнения (14).
Для линейного однородного дифференциального уравнения второго порядка
y''+ a1 (x) y'+ a2( x) y = 0
16

общее решение имеет вид:
y = c1 y1 (x) + c2 y2( x) ,
где y1 (x) и y2 (x) – два линейно независимых решения (фундаментальная система).
Если для такого уравнения известно одно частное решение y1 (x) , то второе его частное решение линейно независимое с первым, можно
найти по формуле, являющейся следствием формулы Лиувилля – Остроградского
e− ∫ a1 ( x) dx
y2 (x) = y1( x) ∫ y12 (x) dx .
Таким образом, общее решение исходного уравнения имеет вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
∫ a1 ( x) dx |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
y = c1 y1 + c2 y1 ∫ |
e |
dx |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y 2 (x) |
|
|
|
|
|
|||||||||||||||||||||||||||||||
и называется формулой Абеля. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Пример 1. Найти общее решение уравнения (1 − |
x2 )y''− |
2xy'+ 2 y = |
0 . |
||||||||||||||||||||||||||||||||||||||||||||||
Решение. Непосредственной проверкой убеждаемся, что это уравне- |
|||||||||||||||||||||||||||||||||||||||||||||||||
ние имеет частное решение y1 = |
|
|
x . Найдем общее решение с помощью |
||||||||||||||||||||||||||||||||||||||||||||||
формулы Абеля, заметив, что a |
(x) = |
|
|
− |
2x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
1− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
2x |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
e∫ |
|
dx |
|
|
|
e− ln |
|
1− x2 |
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
||||||
2 |
|
∫ |
1− x2 |
|
|
∫ |
|
|
|
|
|
∫ |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
2 |
|
|
|
|
|
|
|||||||||
y = |
x |
|
|
x |
|
|
dx = |
x |
|
x |
|
|
dx |
= |
x |
|
|
|
x |
|
1− x |
|
|
|
= x |
|
± |
|
x |
|
|
+ |
2(1− x) |
+ |
2(1+ x) |
dx = |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
± |
1 |
|
+ |
1 |
|
|
|
|
1+ |
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
ln |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
1− |
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 + |
|
|
x |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Общее решение имеет вид: y = |
c1 x + |
|
|
c2 |
|
|
|
|
x ln |
|
|
|
|
|
± |
1 . |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
2 |
|
1− |
|
|
x |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
§6. ЛИНЕЙНОЕ ОДНОРОДНОЕ УРАВНЕНИЕ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Линейным однородным уравнением n-го порядка с постоянными коэффициентами называется уравнения вида:
y(n) + a1 y( n− 1) + a2 y( n− 2) + ... + an y = 0 , |
(15) |
где a1 ,a2 ,...,an – некоторые действительные числа.
17
Для нахождения частных решений составляют характеристическое уравнение
k n + a1k n− 1 + ... + an− 1k + an = 0 , |
(16) |
которое получается из уравнения (15), если искать частные решения этого
уравнения в виде y = ekx (метод подбора решений).
Уравнение (16) является уравнением n-й степени и имеет n корней действительных или комплексных, среди которых могут быть и равные.
Частные решения уравнения (15) зависят от вида корней характеристического уравнения (16), и при их нахождении полезно использовать следующую табл. 1.
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
|
|
|
|
Характер корня характеристического |
|
|
Частные решения |
|
|
|||||||||
|
|
|
|
уравнения (16) |
|
|
|
уравнения (15) |
|
|
|
||||
|
1) k – простой вещественный |
|
|
|
|
|
ekx |
|
|
|
|
|
|||
|
|
|
корень |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2) k – вещественный корень |
|
|
e kx , xe kx , x 2 e kx ,..., x r − |
1 e kx |
|
|
||||||||
|
|
|
кратности r |
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
α |
± β i |
– комплексно сопряженные |
|
|
e α x cos |
β |
x , e α x |
sin β |
x |
|
|
||
|
|
|
корни |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eα |
x cos β |
x , |
|
|
x (r − 1)eα |
|
|
|
|
|
4) |
α |
± β i |
– комплексно сопряженные |
|
|
xe α |
x cos |
β |
x,..., |
x cos |
β x |
|
||
|
|
|
корни кратности r |
|
eα |
x sin β x, |
|
|
x (r − 1)eα |
|
|
|
|||
|
|
|
|
|
|
|
xe α |
x sin |
β |
x,..., |
x sin β |
x |
|
||
|
|
Общее решение уравнения (15) записывается |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
y = c1 y1 + c2 y2 + ... + |
cn− 1 yn− 1 + cn yn , |
|
|
|
|
|
|
||||
где |
y1 , y2 ,..., yn – n частных линейно независимых решений, |
образующих |
|||||||||||||
фундаментальную систему, а c1 ,c2 ,...,cn – произвольные постоянные. |
|
|
|||||||||||||
|
|
Пример 1. Найти общее решение уравнения |
y'''− |
y''+ 4 y'− 4 y = 0 . |
|
|
|||||||||
|
|
Решение. Запишем характеристическое уравнение и найдем его корни. |
|||||||||||||
|
k3 − k2 + 4k − 4 = 0 , k 2 (k − 1) + 4( k − 1) = 0, |
(k 2 + |
4)(k − 1) = 0 , |
k1 = |
1, |
k2,3 |
= ± 2i . |
|
|
||||||
Все корни простые, следовательно, согласно табл. 1 соответствующие частные решения запишутся: y1 = ex , y2 = cos2x, y3 = sin 2x .
Общее решение имеет вид: y = c1ex + c2 cos 2x + c3 sin 3x .
18
Пример 2. Найти общее решение уравнения |
yV + 9 y''' = |
0 . |
|
||||||||
Решение. Напишем характеристическое уравнение |
k 5 + 9k 3 |
= 0 , где |
|||||||||
k1 = 0 корень кратности r = |
3 , |
k2,3 |
= |
± 3i . |
|
|
|
|
|
|
|
Частные решения: |
y1 = e0 x |
= 1 , |
y2 |
= |
x , |
y3 = x2 , y4 = |
cos3x , |
y5 |
= |
sin 3x . |
|
Общее решение: |
y = c1 + c2 x + |
c3 x2 + |
c4 cos3x + c5 sin 3x . |
|
|
|
|
||||
Пример 3. Найти частное решение уравнения y'''− |
3y''+ |
3y'− y = |
0 , удов- |
||||||||
летворяющее начальным условиям y(0) = 1, y'( 0) = 2, y'(' 0) = |
3 . |
|
|
|
|||||||
Решение. Характеристическое |
уравнение |
k 3 − 3k 2 + |
3k − 1 = 0 |
имеет |
|||||||
единственный корень k=1 кратности r=3, поэтому частные решения запишутся y1 = ex , y2 = xex , y3 = x2 ex . Следовательно, y = (c1 + c2 x + c3 x2 )ex – общее решение уравнения.
Для определения произвольных постоянных найдем производные
y'= (c1 + c2 x + c3 x2 )ex + (c2 + 2c3 x)ex , y''= (c1 + c2 x + c3 x2 )ex + 2(c2 + 2c3 x)ex + 2c3ex .
Подставляя начальные условия, получим систему уравнений:
c1 |
= |
1 |
|
|
|
||
|
c1 |
+ |
c2 |
= |
2 |
|
|
|
|
||||||
|
c |
+ |
c |
2 |
+ |
2c |
= 3. |
|
1 |
|
|
|
3 |
|
|
Откуда c1 = 1,c2 |
= 1,c3 = 0 . Следовательно искомое частное решение имеет вид |
|||||||||||||||||||
|
|
|
|
|
|
y = |
(1+ |
x)ex . |
|
|
|
|
|
|
|
|
|
|||
Пример 4. Найти общее решение уравнения |
0 . |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
yVI − 4 yV + 8IV − |
8 y III |
+ 4 yII = |
|
|
|
|
|
|
|
||||||
Решение. Составим характеристическое уравнение |
|
|
|
|
|
|||||||||||||||
и найдем его корни. |
|
k6 − 4k5 + 8k4 − 8k3 + 4k2 = 0 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0, k2 (k2 − |
2k + 2)2 = 0. |
|||||||
Имеем k2 (k4 − |
4k3 + |
8k2 − |
8k + 4) = |
0 , |
k2 (k4 + |
4k2 + |
4 − 4k3 + |
4k2 − 8k)= |
||||||||||||
Откуда k1 = k2 |
= |
0, k3 = k4 |
= 1+ i, k5 = |
k6 |
= 1 − i . |
|
|
|
|
|
|
|
|
|
|
|||||
Частные решение имеют вид: |
1, x, |
ex cos x, ex sin x, |
xex cos x, |
|
xex sin x . |
|
||||||||||||||
Общее решение запишется: |
y = |
c1 + |
c2 x + |
ex (c3 cos x + |
c4 sin x + |
c5 xcos x + |
c6 xsin x) . |
|||||||||||||
Пример 5. Найти общее решение уравнения |
yV + |
2 y = |
0 . |
|
|
|||||||||||||||
Решение. |
Корни характеристического уравнения k 5 + |
2 = 0 |
находим по |
|||||||||||||||||
формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k = |
5 |
− 2 = 5 2(cosπ+ |
isinπ) = |
5 |
|
cos |
π+ 2 πk |
+ i sin |
π+ 2 π k |
|
||||||||
|
|
|
|
2 |
5 |
|
|
|
5 |
, |
|
|||||||||
при k = 0,1,2,3,4 |
|
имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
19
