
- •Министерство образования и науки украины
- •Третий модуль Тема 3. Корреляционно-регрессионный анализ данных наблюдений
- •Последовательность проведения корреляционно-регрессионного анализа
- •Введение в тему
- •Последовательность проведения корреляционно-регрессионного анализа
- •3.2. Проверка данных статистического наблюдения на наличие выбросов
- •3.3. Общие сведения из корреляционно-регрессионного анализа
- •3.4. Форма корреляционной связи
- •3.5. Теснота корреляционной связи
- •Проверка на тесноту связи
- •3.6. Сила корреляционной связи
- •3.7. Методикаполученияуравнений линейной регрессии в случае малых выборок Последовательность проведения регрессионного анализа
- •Технологияопределения в среде эт коэффициентовлинейнойрегрессии в случае малых выборок
- •Прогнозирование на основе полученной модели регрессии
- •3.8. Понятие о многомерном корреляционном анализе
- •Определение Для расчета используем ту же матрицу третьего порядка. Расчет ведем по формуле:
- •Коэффициент множественной корреляции
- •3.9. Создание математических моделей регрессии
- •Парный нелинейный регрессионный анализ
- •Экономический смысл коэффициентов регрессии
- •Многомерный нелинейный регрессионный анализ
- •3.10. Методика получения уравнений парной линейной регрессии при большом объеме выборки
- •3.11. Понятие о мультиколлинеарности
- •Тесты для самоконтроля
- •Характеристика тестов темы 3:
- •Контрольные задания
Экономический смысл коэффициентов регрессии
Многомерный
регрессионный анализ позволяет
разграничить влияние факторных признаков.
Параметр регрессии
![]() при каждом факторном признаке
при каждом факторном признаке![]() дает оценку его влияния на величину
результативного признака
дает оценку его влияния на величину
результативного признака![]() в случае изменения
в случае изменения![]() на единицу при постоянстве всех
остальных факторов.
на единицу при постоянстве всех
остальных факторов.
Прогнозирование на основе полученной моделивыполняется аналогично прогнозам парной линейной регрессии.
Точечный
прогнозполучается при подстановке
прогнозных значений факторных признаков![]() в уравнение регрессии. Полученное
значение
в уравнение регрессии. Полученное
значение
![]() является
точечным прогнозом
результативного признака
является
точечным прогнозом
результативного признака![]() .
.
Интервальный
прогнозуказывает нижнюю и верхнюю
границу промежутка, в котором находится
истинное значение прогнозируемого
показателя![]() .Доверительный интервал определяется
выражением
.Доверительный интервал определяется
выражением
![]() ,
,
т.е. истинное значение
прогнозируемого показателя
![]() с вероятностью 1 -принадлежит доверительному интервалу.
с вероятностью 1 -принадлежит доверительному интервалу.
Пример 3.9. По данным таблицы 3.17 записать уравнение регрессии и выполнить анализ полученной модели.
Решение. Так как инструмент «Регрессия» может выполнять только линейный регрессионный анализ, то в итоге имеем следующее уравнение многомерной линейной регрессии
![]() Таблица
3.17. Результаты работы инструментаРегрессия
Таблица
3.17. Результаты работы инструментаРегрессия

Выполним анализ полученной модели регрессии:
коэффициент множественной корреляции равен 0,7084, следовательно, между результативным признаком и данными факторными признаками наблюдается сильная корреляционная связь;
коэффициент множественной детерминации
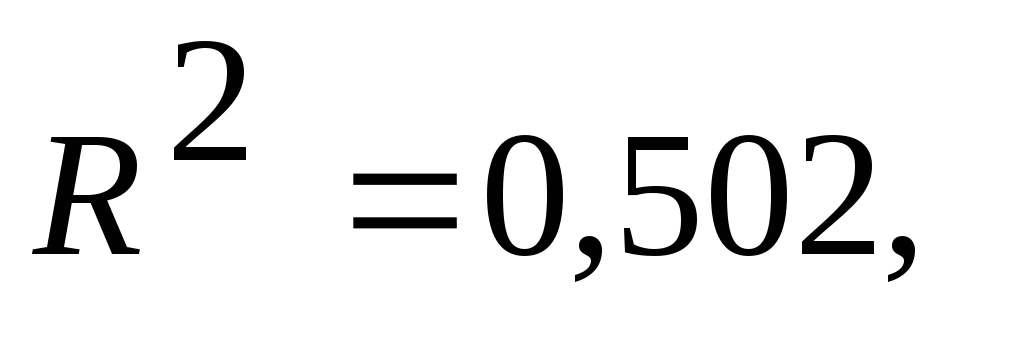 т.е.
только 50,2% дисперсии результативного
признака связано с данными факторными
признаками;
т.е.
только 50,2% дисперсии результативного
признака связано с данными факторными
признаками;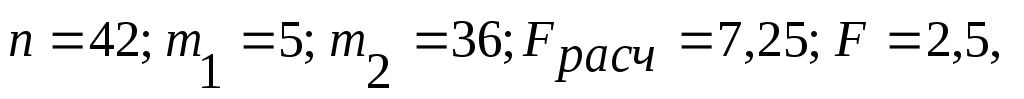 т.е.
расчетное значение критерия Фишера
больше критического значения и,
следовательно, уравнение регрессии в
целом статистически значимо и наблюдается
хорошее соответствие данным наблюдений;
т.е.
расчетное значение критерия Фишера
больше критического значения и,
следовательно, уравнение регрессии в
целом статистически значимо и наблюдается
хорошее соответствие данным наблюдений;критическое значение
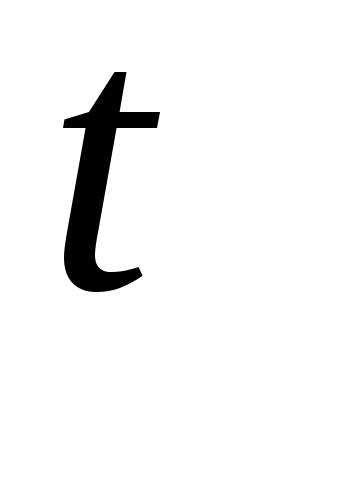 - статистики при уровне значимости
- статистики при уровне значимости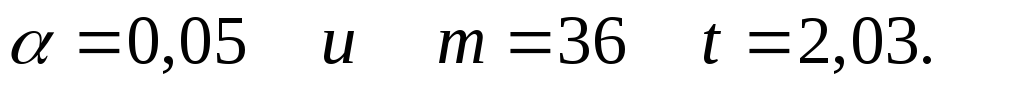 Только для двух коэффициентов, стоящих
при
Только для двух коэффициентов, стоящих
при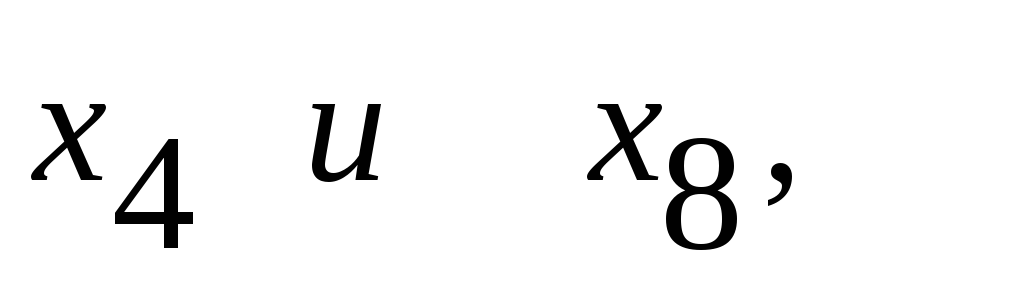 расчетные значения
расчетные значения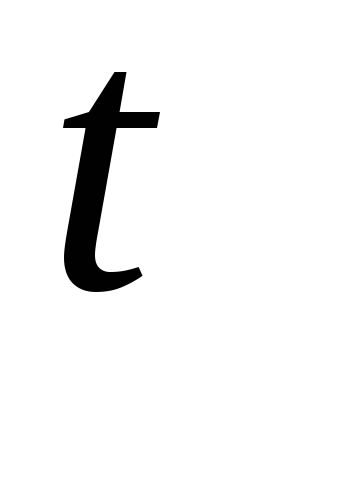 - статистики больше критического, т.е.
эти коэффициенты статистически значимы,
что подтверждается
- статистики больше критического, т.е.
эти коэффициенты статистически значимы,
что подтверждается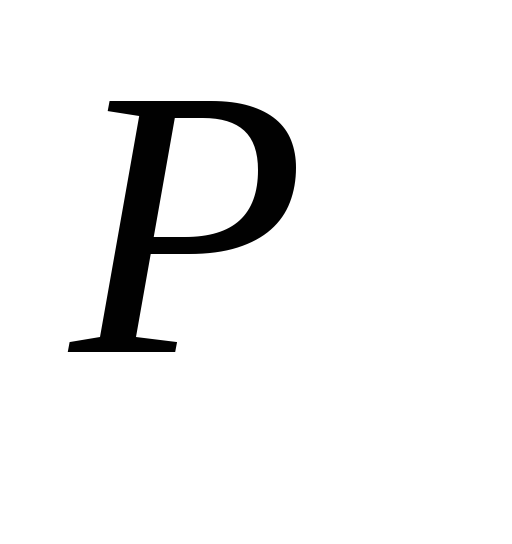 -
значениями и границами доверительного
интервала. Для остальных коэффициентов
нет причин отвергать нулевую гипотезу,
так как они могут принимать нулевые
значения. Об этом свидетельствуют
знаки границ доверительного интервала
каждого из этих коэффициентов.
-
значениями и границами доверительного
интервала. Для остальных коэффициентов
нет причин отвергать нулевую гипотезу,
так как они могут принимать нулевые
значения. Об этом свидетельствуют
знаки границ доверительного интервала
каждого из этих коэффициентов.
Следовательно, модель регрессии пригодна для принятия некоторых решений, но не для прогнозирования.
Проанализируем наличие парной корреляционной связи между факторными признаками, входящими в модель регрессии, по корреляционной матрице (рис.3.8):
наблюдается очень сильная связь между факторными признаками
 так
как коэффициент парной корреляции
между ними равен 0,97. Следовательно, в
многомерную модель регрессии включать
их вместе нельзя;
так
как коэффициент парной корреляции
между ними равен 0,97. Следовательно, в
многомерную модель регрессии включать
их вместе нельзя;
между признаками
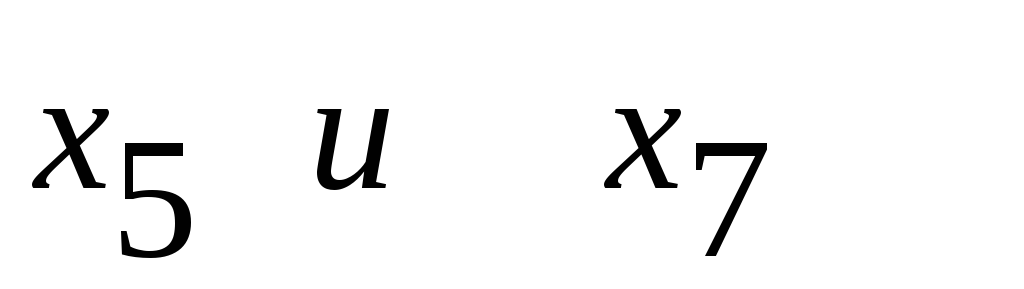 ,
а также между
,
а также между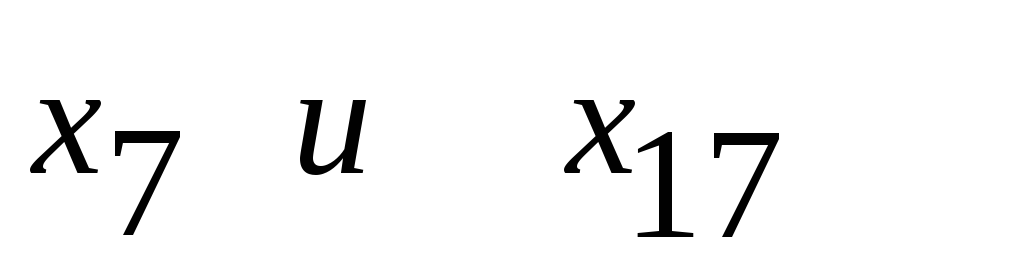 связь
умеренная;
связь
умеренная;признаки
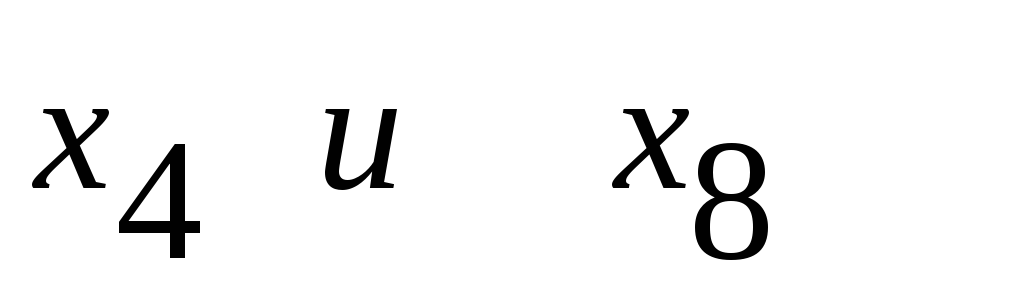 независимы
между собой;
независимы
между собой;между результативным признаком
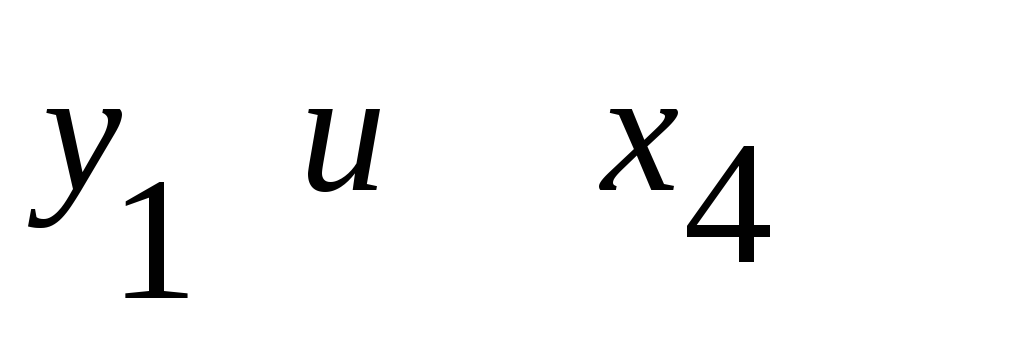 наблюдается
заметная связь, а между
наблюдается
заметная связь, а между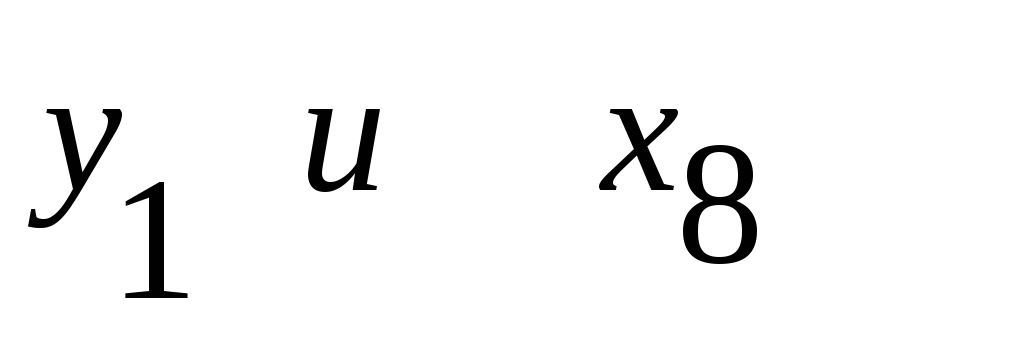 -
умеренная. С остальными факторными
признаками связь практически отсутствует.
-
умеренная. С остальными факторными
признаками связь практически отсутствует.

Рис.3.8. Корреляционная матрица
Обозначения
к корреляционной матрице:
![]() -
производительность труда (среднегодовая
выработка продукции на одного работника),
тыс. грн.;
-
производительность труда (среднегодовая
выработка продукции на одного работника),
тыс. грн.;![]() -
трудоемкость единицы продукции;
-
трудоемкость единицы продукции;![]() -
удельный вес рабочих в составе
промышленно-производственного персонала;
-
удельный вес рабочих в составе
промышленно-производственного персонала;![]() -коэффициент
сменности оборудования;
-коэффициент
сменности оборудования;![]() -
премии и вознаграждения на одного
работника, %;
-
премии и вознаграждения на одного
работника, %;![]() -
непроизводственные расходы, %.
-
непроизводственные расходы, %.
Следовательно, на основе исследуемой многомерной выборки можно сделать вывод, что из рассматриваемых факторных признаков на производительность труда оказывают влияние трудоемкость единицы продукции и премии. Эти факторные признаки следует включить в модель многомерной нелинейной регрессии.
Так как коэффициент детерминации сравнительно мал, то при разработке модели регрессии следует рассмотреть дополнительные неучтенные факторные признаки.
В
таблице 3.18 приведены результаты работы
инструмента «Регрессия» для модели
регрессии без факторного признака
![]() Выполните
анализ этой модели регрессии.
Выполните
анализ этой модели регрессии.
