3.9. Создание математических моделей регрессии

Предметом регрессионного анализа является исследование зависимости случайной величины от совокупности случайных и неслучайных величин. Регрессионный анализ позволяет на основе выборочных наблюдений создать математическую модель зависимости результативного признака от факторных признаков.

В зависимости от количества факторных признаков модель регрессии может быть парной и многомерной. Запишем в общем виде зависимость результативного признака от совместного и одновременного влияния факторных признаков(- количество факторных признаков)

(3.28)

где - функция регрессии, которая выражает объективную закономерную зависимость результативного признака от совместного влияния факторных признаков;- случайная величина, выражающая влияние неконтролируемых и неучтенных факторов, а также ошибок измерения.

Из выражения (3.28) имеем

(3.29)

т.е. - отклонение результативного признака от среднего значения, вычисленного по функции регрессии.

Оценкой функции регрессии является уравнение регрессии

(3.30)

Для парной линейной регрессии выражение (3.28) имеет вид:

(3.31)

где - параметры функции регрессии. Запишем уравнение регрессии для этого случая

(3.32)

где - оценки параметров функции регрессии - параметры уравнения регрессии или просто параметры регрессии.

Методика получения уравнений парной линейной регрессии приведена в параграфах 3.7 и 3.10.

Парный нелинейный регрессионный анализ

Пусть по виду корреляционного поля точек предполагается нелинейная зависимость результативного признака от факторного признака. Запишем в общем виде уравнение парной нелинейной регрессии

(3.33)

Требуется определить параметры регрессии с помощью метода наименьших квадратов, математическая запись которого имеет вид:

(3.34)

и надстройки «Поиск решения».

Размещение информации на рабочем месте ЭТ при определении параметров регрессии примера 3.5 с помощью надстройки “Поиск решения” представлено в таблице 3.15.

Таблица 3.15. Размещение информации

	A	B	C	D	E	F	G	H	I
1	a0	a1	a2	Значение целевой функции
2						=*		=*	=*
3	1	х	x^2	y	Yx	e	e^2	e1	e1^2
4	1	2,5	=b4^2	78	=*	=d4-e4	=f4^2	=d4-$i$2	=h4^2
5	1	2,6		80
18	1	4		105
19
20	15	3	2	=a20-c20-1			=g19/(a20-b20)		=i19/ (a20-b20)
21							=1-g20/ i20		=g21* d20/((1-g21)* c20)
22								F=	3,88

F2: = СУММКВРАЗН (e4:e18; d4:d18);

E4: = СУММПРОИЗВ(a4:c4;$a$2:$c$2);

H2: =КОРРЕЛ(d4:d18;e4:e18);I2: =СРЗНАЧ(d4:d18).

Результаты решения представлены в таблице 3.16.

Таблица 3.16. Результаты расчета

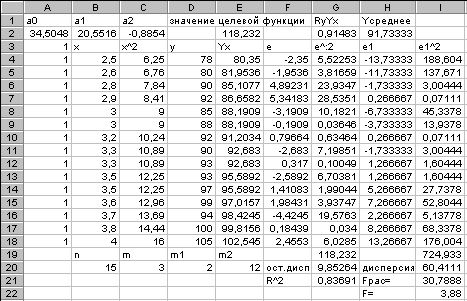Анализ результатов расчета. В итоге расчета получено:

• уравнение парной нелинейной регрессии

• коэффициент корреляции 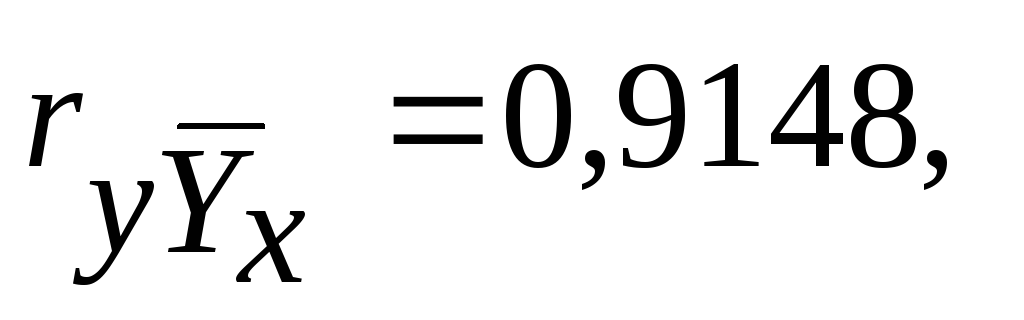что свидетельствует о высоком качестве полученной модели регрессии;

• коэффициент детерминации 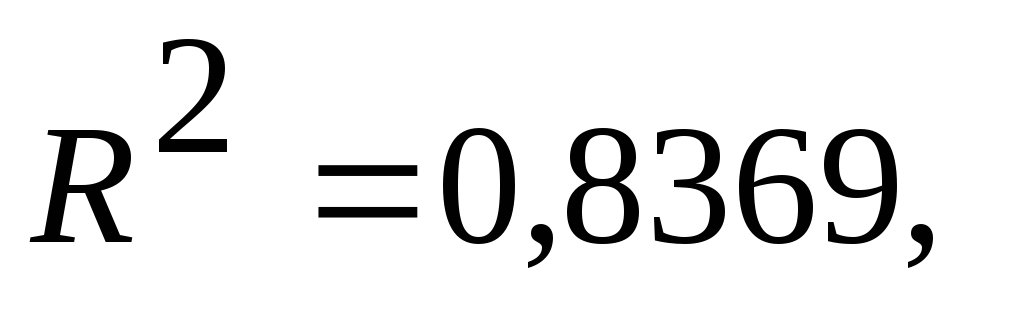т.е. 83,7% изменчивости стоимости внутренней площади оцениваемого объекта недвижимости связано с арендной платой;

• расчетное значение критерия Фишера больше критического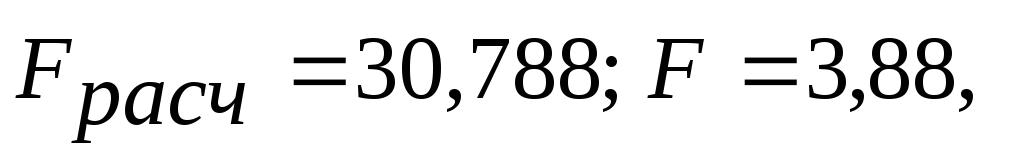следовательно, уравнение регрессии можно использовать для прогнозирования.

На рис.3.7 представлено уравнение парной нелинейной регрессии, полученное путем построения линии тренда. Анализ уравнений подтверждает их идентичность. Сравнение результатов расчета при парном линейном и нелинейном регрессионном анализе показывает, что они отличаются незначительно, т.е. для рассматриваемых признаков можно принять линейную модель регрессии.

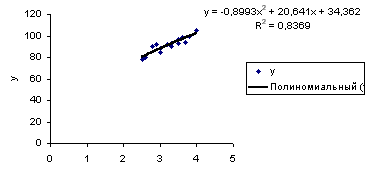
Рис. 3.7. Уравнение линии тренда

Многомерный линейный регрессионный анализ

Обобщенная математическая модель многомерной линейной функции регрессии (3.28) имеет вид

(3.36)

где – количество факторных признаков;– результативный признак;– отклонение;– параметры функции регрессии.

Уравнение многомерной линейной регрессии для этого случая

. (3.37)

Требование к факторным признакам, включаемым в математическую модель: факторы должны быть независимы друг от друга. Нарушение этого условия называется мультиколлинеарностью.

Коэффициенты уравнения регрессии получают с помощью инструмента «Регрессия» пакета анализа.

Анализ качества полученной моделипроводится аналогично анализу парной линейной регрессии.