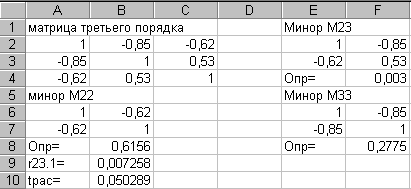
Определение Для расчета используем ту же матрицу третьего порядка. Расчет ведем по формуле:

Результаты расчета в среде ЭТ представлены в таблице 3.10. Частный коэффициент корреляции Оценим статистическую значимость частного коэффициента корреляции. Расчетное значение- статистикиКритическое значение - равно 2.

Так как расчетное значение - статистики меньше критического, то нет причин отвергать нулевую гипотезу.

Частный коэффициент корреляции показывает, что при фиксированном значении признака корреляция между признакамииотсутствует.

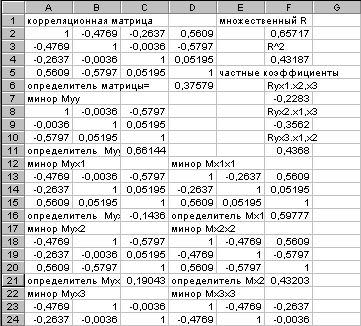
Таблица 3.10. Результаты расчета

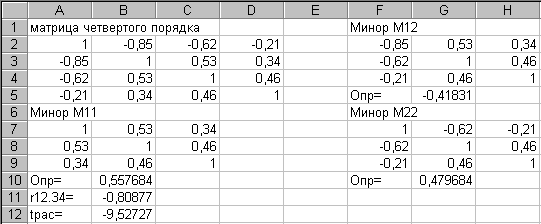
Определение частного коэффициента корреляции второго порядка Расчетная формула имеет вид:

(3.26)

Результаты расчета в среде ЭТ представлены в таблице 3.11. Значения миноров получены с помощью матричной функции МОПР мастера функций. Для рассматриваемого примера имеем следующие алгебраические дополнения: Тогда частный коэффициент корреляции

Таблица 3.11. Результаты расчета

Оценим значимость частного коэффициента корреляции.

Следовательно, нулевую гипотезу отвергаем. Можно говорить о наличии корреляционной связи между признакамиипри фиксированном значении признакови

Коэффициент множественной корреляции

Часто представляет интерес оценить связь одного из признаков со всеми остальными. Делается это с помощью коэффициента множественной корреляции

(3.27)

где - определитель корреляционной матрицы- алгебраическое дополнение к элементу

Оценкой коэффициента множественной корреляции является выборочный коэффициент множественной корреляции, определяемый по формуле

(3.28)

где - определитель корреляционной матрицы- алгебраическое дополнение к элементуКвадраты соответствующих коэффициентов множественной корреляции называют коэффициентами множественной детерминации и обозначают соответственно

Детерминация выражает долю дисперсии в исследуемом признаке, связанную с дисперсией в остальных признаках. Например, исследуется зависимость рентабельностипредприятия от признака- «премии и вознаграждения» и получено=0,458. Это означает, что примерно 45,8% меры изменчивости рентабельности связано с мерой изменчивости признака «премии и вознаграждения». В случае исследования трех переменных и более, как правило,>и показывает, что когда оптимальным образом соединяются остальные признаки в соответствии с уравнением регрессии, то это оказывает благотворное влияние на результативный признак. Рис.3.6 представляет геометрический смысл коэффициента детерминации.

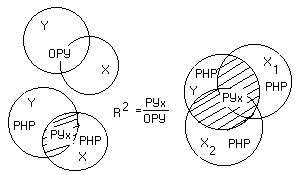
Рис. 3.6. Геометрический смысл коэффициента детерминации

Пример 3.7. Определить оценки коэффициентов множественной корреляции и детерминации первого признака со всеми остальными, используя данные примера 3.6.

Расчетная формула в этом случае имеет вид:

Результаты расчета в среде ЭТ представлены в таблице 3.12.

Статистическую значимость коэффициентов множественной корреляции и детерминации проверяют с помощью критерия Фишера. Проверяется нулевая гипотеза Для этого вычисляют статистику, имеющую- распределение сстепенями свободы (- число фиксированных признаков).

Таблица 3.12. Результаты расчета

По приложению 2 [10] находят критическое значение критерия Фишера. Если расчетное значение критерия Фишера больше критического, то нулевая гипотеза отвергается. В противном случае нет причин отвергнуть нулевую гипотезу.

Для рассматриваемого примера Нулевая гипотеза отвергается. Следовательно, можно говорить о корреляционной связи признакас остальными признаками.

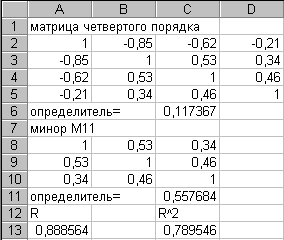
Пример 3.8. Для многомерной выборки объектов недвижимости получена корреляционная матрица, представленная в таблице 3.13. Обозначения в этой таблице:

• - стоимость 1м² внутренней площади, у.е.;

• - величина физического износа, %;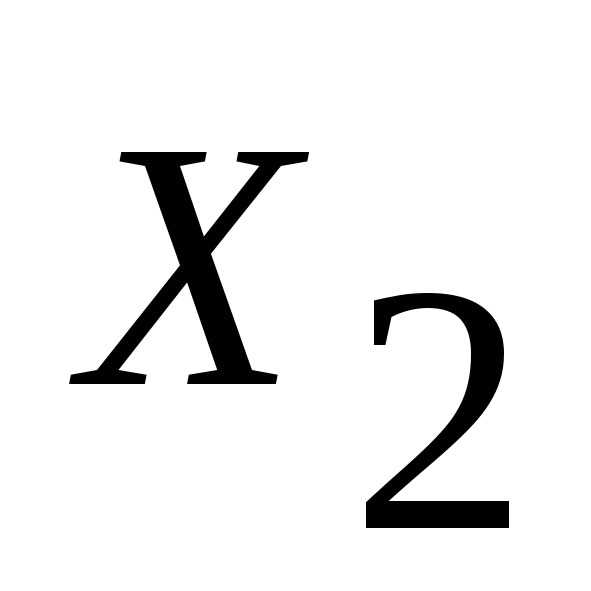

• - доля подвальных помещений в общей площади;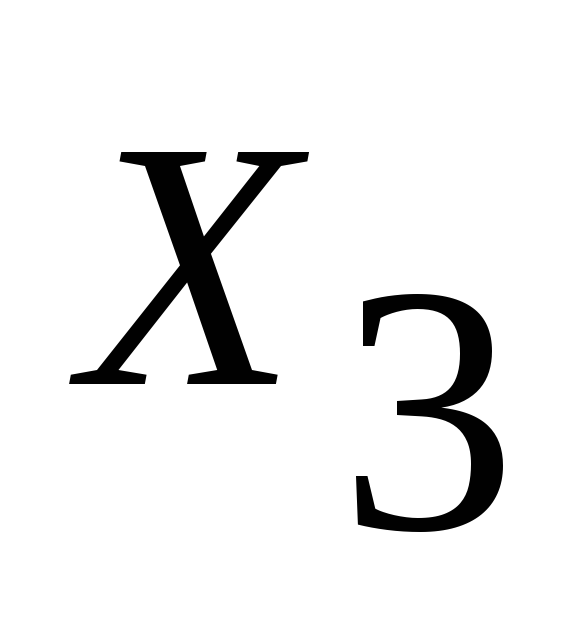

• - стоимость улучшений на 1м² внутренней площади, у.е.

Таблица 3.13. Корреляционная матрица

	1	-0,47691	-0,26374	0,560895
	-0,47691	1	-0,00362	-0,57971
	-0,26374	-0,00362	1	0,051953
	0,560895	-0,57971	0,051953	1

Определить выборочные частные коэффициенты корреляции результативного признака с каждым факторным признаком и коэффициенты множественной корреляции и детерминации.

Решение. Расчетные формулы в данном случае имеют вид:

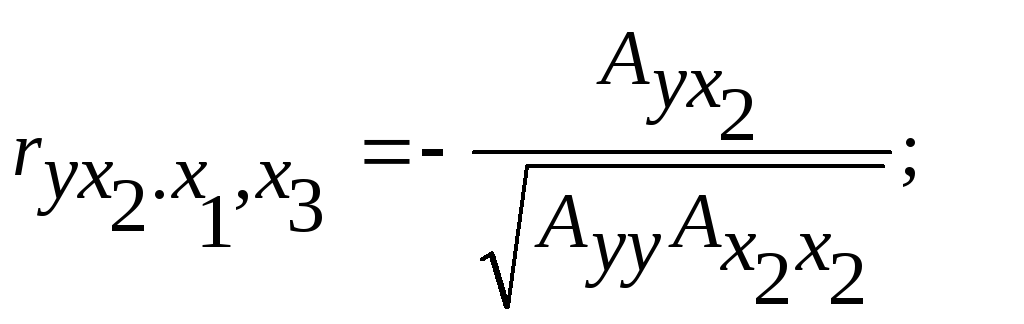
В таблице 3.14 приведены результаты расчета в среде ЭТ.

Сравнение частных коэффициентов корреляции с соответствующими коэффициентами парной корреляции показывает, например, что в парной корреляции между стоимостью 1 м² и величиной износа высока доля влияния остальных признаков, так как частный коэффициент корреляции меньше парного (). Это можно объяснить тем, что среди зданий с высоким уровнем износа в выборке чаще встречаются подвальные помещения, на реставрацию которых мало кто желает вкладывать средства.

Величина коэффициента множественной корреляции показывает, что наблюдается заметная связь между стоимостью 1 м² внутренней площади недвижимости и показателями уровня износа, доли подвальных помещений в общей площади, стоимости улучшений на 1 м² . Коэффициент множественной детерминации показывает, что только 43,2% общей дисперсии стоимости 1 м² внутренней площади недвижимости объясняется влиянием исследуемых факторных признаков. Следовательно, в математической модели регрессии не учтены еще важные факторные признаки.

Таблица 3.14. Результаты расчета