37. Формула интегрирования по частям для определенного интеграла.

Если ф-ции u(x) и v(x) и их призводные u(x) и v (x) непрерывны в промежутке a x  b ,то ф-ла интегрирования по частям для опред. интеграла имеет вид:

38. Применение определенного интеграла в экономике

Пусть функция z=f(t) описывает изменение производительности некоторого производства с течением времени. Найдем объем продукции u, произведенной за промежуток времени [0,T].

Отметим, что если производительность не изменяется с течением времени (f(x)– const), то объем продукции Δu, произведенной за некоторый промежуток времени [t,t+Δt], задается ф-лой Δu=f(t)Δt. В общем случае справедливо приближенное равенство Δu=f(ξ)Δt, где ξ Є [t,t+Δt], которое оказывается тем более точным, чем меньше Δt.

Разобьем отрезок [0,T] на промежутки времени точками: 0=t₀<t₁<t₂<…<t_n=T. Для величины объема продукции ∆u_i, произведенной за промежуток времени [t_i-1, t_i], имеем

∆u_i=f(ξ_i)∆t_i, где ξ_i Є [t_i-1, t_i], Δt=t_i– t_i-1, i= 1, 2, …, n. Тогда

.

При стремлении max Δt_i к нулю каждое из использованных приближенных равенств становится все более точным, поэтому.

Учитывая определение определенного интеграла, окончательно получаем

,

т.е. если f(t) – производительность труда в момент t, то есть объем выпускаемой продукции за промежуток [0,T].

Величина объема продукции, произведенной за промежуток времени [0,T], численно равна площади под графиком функции z=f(t), описывающей изменение производительности труда с течением времени, на промежутке [0,T] или .

39. Применение определенного интеграла для вычисления площадей фигур, длин дуг плоских кривых и объемов тел.

Прилож.№1: вычисление S-ей плоских фигур.

А) S фигуры в декартовой сис-ме корд-т; S криволин. трапеции:

♦ располож. выше оси ОХ (f(x)≥0, x€[a;b]): S=

♦ ниже ОХ (f(x)<0, x€[a;b]): S=−f(x)dx;

Б) Если плоская ф-ра опис-ся 2-мя кривыми(f₂(x)≤f₁(x)):

S=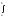f₁(x)dx−f₂(x)dx;

(Если плоская ф-ра имеет сложную форму, то прямыми, ║оси ОУ, ее следует разбить на части так, чтобы м-но было применить известные формулы.)

В) Если криволин. трапеция ограничена прчмыми: у=с, у=d, х=0, у=φ(х)≥0, то удобнее рассмотреть дифф-л по у: S=f(x)dy;

Прилож.№2: криволин. трап. задана параметрически, т.е. трапеция ограничена прямыми t€[α;β] ; x=a; x=b; y=0 :

S=│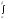y(t)·x'(t)dt │;

Прилож.№3: в полярной сис-ме координат. S фигуры, огранич. непрерывной линией r=r(φ) и 2-мя лучами φ=α, φ=β (при α<β), где r ,φ− полярные координаты. (Зная угол и радиус, определяется точное положение точки на плоскости) : S=½r²(φ)dφ;

40. Приближенные методы вычисления определенных интегралов.

41. Несобственные интегралы.

Опред. нтеграл от а до в ф-ии f(x), где промежуток интегрирования конечен (отрезок), называется собственным интегралом (f(x) непрерывна на [а,в]

Несобственный интеграл-опред. интеграл от непрерыв. ф-ии ,но с бесконечным промежутком интегрирования,или опред. интеграл с конечным промежутком интегрирования, но подинтегр.ф-ия имеет на нем бесконечный разрыв.

Пусть ф-ия f(x) непрерывна на интервале [а,+∞),если сущ-т конечный предел при в+∞,

в

то lim ∫f(x)dх (при в+∞)– несобств. интеграл первого рода

а

+∞ в

∫ f(x)dх= lim ∫f(x)dх (при в+∞)

а а

Если такой предел сущ-т, то говорят, что интеграл сходится,если нет-расход.

Аналогично вводится понятие несобст.инт. от (-∞,в]

42. Определение двойного интеграла.

43. Геометрический смысл двойного интеграла.

44. Сведение двойного интеграла к повторному.

45. Тройной интеграл.

46. Приложения кратных интегралов.

47. Основные понятия теории обыкновенных дифференциальных уравнений.

48. Задача Коши.

49. Теорема существования и единственности решения.

50. Составление дифференциального уравнения первого порядка.

51. Модели экономической динамики.

52. Дифференциальные уравнения первого порядка.

53. Методы интегрирования дифференциальных уравнений первого порядка.

54. Линейные дифференциальные уравнения первого порядка.

55. Линейные дифференциальные уравнения высших порядков.

56. Однородные и неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью.

57. Метод Лагранжа вариации произвольной постоянной.

58. Системы линейных дифференциальных уравнений второго порядка с постоянными коэффициентами.

59. Понятие числового ряда.

60. Сходимость числового ряда.

61. Простейшие свойства сходящихся рядов.

62. Необходимое условие сходимости числового ряда.

63. Признаки сходимости рядов с положительными членами.

64. Знакопеременные ряды.

65. Абсолютная и условная сходимость.

66. Знакочередующиеся ряды.

67. Признак Лейбница.

68. Функциональные ряды.

69. Степенные ряды.

70. Теорема Абеля.

71. Область и интервал сходимости степенного ряда.

72. Ряды Тейлора и Маклорена.

73. Разложение элементарных функций в степенные ряды.

74. Применение рядов к приближенным вычислениям.

75. Ряды Фурье.

76. Разложение функций в ряды Фурье.