25. Метод замены переменной.

Сущность интегрирования методом замены переменной заключается в преобразовании аргумента подынтегральной функции по некот. формуле, рассчитанной на то, чтобы интеграл в новой переменной оказался проще для вычисления.

x=φ(t); dx=φ’(t)dt; =

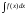Пример:(3x+2)⁵ dx ?

Замена:

3x+2=t

3dx=dt ; dx=1/3dt

Подставляем:

(3x+2)⁵dx=1/3t⁵dt=1/3*t⁶/6+C=1/18*t⁶+C

Заменив t через x получаем:

(3x+2)⁵dx=1/18*t⁶+C=1/18(3x+2)⁶+c

26. Формула интегрирования по частям.

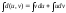
uv=

Пример.[u=x,du=dx,dv=sinxdx,v=-cosx]=-xcosx+=-xcosx+sinx

Метод интегрир-я по частям не каждый раз и не при всяком выборе из множителей u и dv дает возможность вычислить заданный интеграл. Умение увидеть целесообр-сть применения этого метода вырабатывается в практике интегрир-я.

27. Таблица неопределенных интегралов.

Табл. неопр-х интегралов нетрудно получить, воспользовавшись тем, что интегр-е явл. операцией, обратной дифференц-ю.

Таблица интегралов

1.;

2.

3.

4.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

28. Интегрирование простейших рациональных дробей.

Здесь имеется в виду след. Дроби:

; , где р(х)—целая рациональная функция

Если мы приведём в правильный вид 1 часть, то получим:

Если приведём в правильный вид 2 часть, то получим:

Если рассмотреть интегралы от функций 1 и 2, то получим:

=А==; решение сводится к сумме 2-х интегралов: или и

29. Интегрирование рациональных функций.

30. Интегрирование иррациональных функций.

31. Интегрирование выражений, содержащих тригонометрические функции.

32. Определенный интеграл.

33. Условия интегрируемости функций.

34. Формула Ньютона-Лейбница.

Для вычисления опред. интеграла от ф-ции f(x) в том случае,когда можно найти соответствующий неопред. интеграл F(x),служит ф-ла Ньютона-Лейбница:

т.е. опред. интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.

35. Основные свойства определенного интеграла.

1. постоянную можно выносить из-под знака опред. интеграла: = a

2. интеграл суммы функций равен сумме интегралов: = +

3. если на отрезке [a;b] для любого х f(x)≤φ(x), то

≤

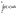
4. если m и М – наим. и наиб. знач. ф-и f(x) на [a;b], то m(b-a)≤ ≤ M(b-a)

5. теорема о среднем: если f(x) непрер. на [a;b], то на этом отрезке найдется такая т. E[a;b], что =(b-a)f(E)

6. для любых 3-х чисел a, b, c справедливо равенство:

=+ ,

если только все эти интегралы существуют

36. Замена переменной в определенном интеграле.

При вычислении оред. интеграла методом замены переменной (способом подстановки) опред. интеграл преобразуется с помощью подстановки u=(x) или x=(u) в опред. интеграл относительно новой переменной u.При этом старые пределы интегрирования a и b заменяются соответственно новыми пределами интегрирования  и ,кот. находятся из исходной подстановки.

Из первой подстановки новые пределы интегрирования вычисляются непосредственно:=(a), =(b).

Из 2-ой подстановки новые пределы интегрирования находятся путем реш. уравн. a=a) и b) относительно  и .

Таким образом,имеем