Вопросы и упражнения для самопроверки.

1. Дайте определение производной функции.

2. В чем состоит геометрический смысл производной?

3. В чем состоит физический смысл производной?

4. Дайте определение второй производной функции.

5. В чем состоит физический смысл второй производ­ной?

6. Напишите все формулы дифференцирования.

7. Сформулируйте условие постоянства функции.

8. Сформулируйте условия возрастания и убывания функции.

9. Сформулируйте необходимое условие существова­ния экстремума функции.

10. Сформулируйте достаточные условия существова­ния экстремума функции.

11. Как найти точки экстремума и экстремумы функ­ции?

12. Как найти наименьшее и наибольшее значения функции на отрезке?

13. Выпуклость функции. Точки перегиба.

14. Общая схема исследования функции.

15. Исследовать функцию и построить график. .

16. Исследовать функцию и построить график. .

17. Исследовать функцию и построить график. .

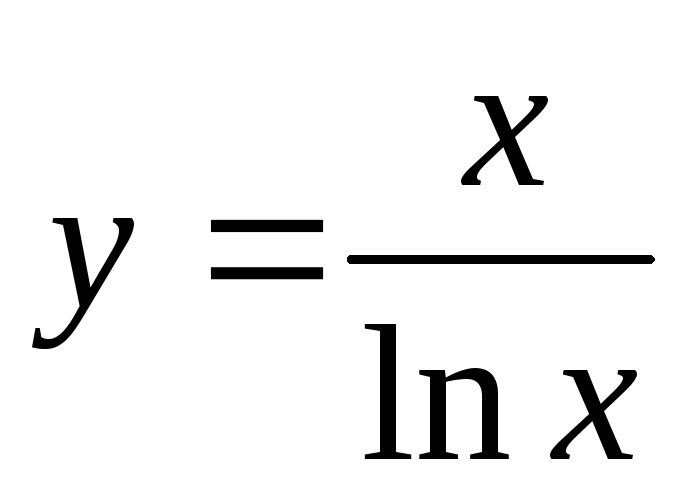18. Найдите производные функций: a) у = (2—z²)⁴; б) y = ln sin² (1—х),

в)

19. Найдите вторую производную функций: a) б)y=ln sin x; в) у=соs х.

20. Составьте уравнение касательной к кривой у=tg2x в начале координат.

21. При каком значении переменной х касательные к кривым у=х² и у=х³ параллельны

4. Дифференциал функции. Функции нескольких переменных

4.1. Понятие дифференциала функции

С понятием производной тесно связано важное понятие математики  по­нятие дифференциала.

Пусть y = f(x) есть некоторая функция, имеющая в определенной точке х производную f (х). Дадим аргу­менту х приращение х, тогда функция получит прира­щение y=f(x+x) - f(x).

По определению производной имеем Так как разность между переменной, имеющей предел, и этим пределом является бесконечно малой, тоесть величина бесконечно малая приx0:

где (х)0 при х0.

Тогда у=f (х)х+ (x)x.

Как видно, если функция y=f(x) имеет производную в точке х, то приращение функции в этой точке состоит из двух слагаемых. Второе слагаемое (х)x как про­изведение двух бесконечно малых величин есть беско­нечно малая более высокого, чем х. Если f (х)=0, то первое слагаемое f' (x)x имеет тот же по­рядок, что и \х. Значит, при малых х второе слагаемое менее важно, чем первое. Это первое слагаемое (неза­висимо от того, будет ли f' (x)=0) и называют диффе­ренциалом.

Дифференциалом функции y=f(x) в точке х назы­вается главная часть f' (x)x приращения функции у, линейно зависящая от приращения аргумента х.

Дифференциал обозначается символом dy. По опре­делению, dy=f' (x)x.

В частности, при f (x)=x получим dx=1x или dx=x, т.е. дифференциал аргумента равен его при­ращению.

Тогда dy = f' (x)dx, т.е. дифференциал функции у=f(x) в точке х равен произведению производной в точ­ке х на дифференциал аргумента.

Отсюда, так чтовыражение, которое мы рань­ше считали цельным символом, теперь можно рассмат­ривать как дробь, равную отношению дифференциала функции к дифференциалу аргумента.

Нахождение дифференциа­ла функции называется диф­ференцированием, так же как и нахождение производной.

Геометрически приращение функции у равно прираще­нию KN ординаты точки кри­вой, а дифференциал функции dy равен соответствен­ному приращению КР орди­наты касательной, проведен­ной к кривой в точке (х, f (x)), когда аргумент получает приращение х.

Пример 1. Найти дифференциал функции у= (2х³-4)⁵.

Решение. Находим производную данной функции:

у = 5 (2х³-4)⁴ (2х³-4) = 5 (2х³-4)⁴  6х² = 30х² (2х³-4)⁴.

Умножив производную на дифференциал аргумента, получим дифференциал функции:

dy = 30х² (2х³-4)⁴ dx.

Пример 2. Найти дифференциал функции

Решение. Сначала найдем производную данной функции:

Умножив производную на дифференциал аргумента, получим дифференциал функции: