4. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ

Тема 4.1. Производная функции

Определение 4.1 Производной функции в точке называется предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю, если этот предел существует и конечен:

или .

Для обозначения производной могут использоваться следующие эквивалентные символы:

.

Операция отыскания производной называется дифференцированием функции. Числовое значение производной функции в точке обозначается .

Теорема 4.1 Если: функция имеет производную в точке то она непрерывна в этой точке.

Обратное утверждение не всегда верно (исключение составляют угловые точки, а также точки возврата и перегиба с вертикальной касательный).

Геометрический смысл производной: производная в точке равна угловому коэффициенту касательной к кривой в точке (рис.4.1).

.

Механический смысл производной: производная есть скорость изменения функции в точке .

Пусть - постоянные; - некоторые дифференцируемые функции, причем - сложная функция по независимому аргументу , а является промежуточным аргументом.

Рис. 4.1

Основные правила дифференцирования

Основные формулы дифференцирования

Если функция задана неявно, т.е. уравнение не разрешено относительно , обе части этого уравнения дифференцируют по , а затем находят .

Если функция задана параметрически в виде

то

Производной -го порядка от функции называется производная от производной -го порядка:

.

Эта производная может обозначаться так

.

Для параметрически заданной функции производная ‑го порядка находится как

.

Задача 4.1 Найти производную функции , исходя из ее определения.

Решение

По определению .

Поэтому дадим аргументу приращение , вычислим приращение функции и найдем предел отношения :

Задача 4.2 Найти производные функций:

а)

б)

в)

г)

д) .

Решение

а)

б)

в)

г) По определению модуля

Тогда

д) Предварительно прологарифмируем обе части равенства, а затем продифференцируем их и помножим на :

Задача 4.3 Найти вторую производную неявно заданной функции

Решение

Введем новую переменную . Тогда уравнение будет выглядеть так:

Дифференцируем обе части уравнения:

Отсюда .

Но

Тогда

Так как то

Задача 4.4 Найти производную -го порядка от параметрически заданной функции:

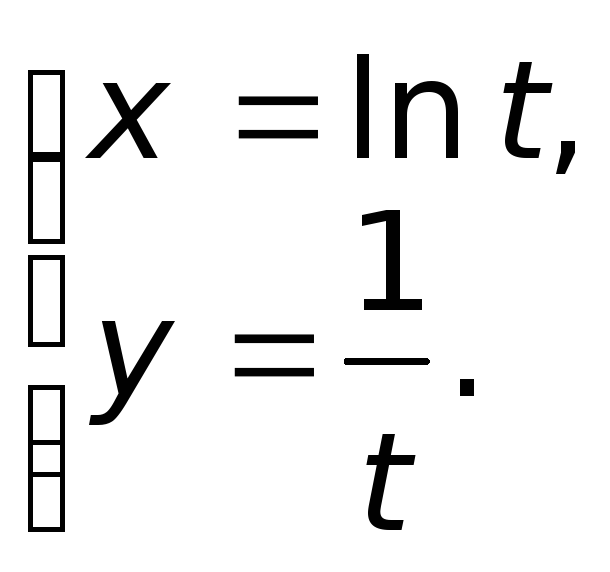
Решение

Для определения. производной -го порядка надо последовательно найти -1 предыдущую производную.

Очевидно, что

Тема 4.2. Дифференциал функции одной переменной

Определение 4.2 Дифференциалом функции называется главная часть ее приращения, линейная относительно приращения аргумента.

Определение 4.3 Дифференциалом аргумента называется приращение этого аргумента: .

Дифференциал функции определяется по формуле

.

Геометрический смысл дифференциала функции в точке : он численно равен приращению ординаты касательной к графику функции в этой точке.

Дифференциал функции используется, для приближенных вычислений:

.

Дифференциал -го порядка определяется как

.

Задача 4.5 Сравнить приращение и дифференциал функции при и .

Решение

Дав аргументу приращение , получим приращение функции :

Отсюда

По определению дифференциала

При заданных х, , а также учитывая, что , получим:

,

Задача 4.6 Найти приближенное значение .

Решение

Если приращение аргумента мало по абсолютной величине, то для приближенных, вычислений можно воспользоваться формулой

.

В примере . Тогда

Тема 4.3. Приложение дифференциального исчисления для исследования функций

Определение 4.4 Функция называется непрерывной при , если она определена в некоторой окрестности и

В противном случае функция в точке имеет разрыв.

Различают следующие виды точек разрыва.

Определение 4.5 Разрыв I рода - когда существуют конечные односторонние пределы и . В свою очередь, среди таких точек выделяют точки устранимого разрыва, если односторонние пределы одинаковы (функцию доопределяют: ), и неустранимого, если .

Определение 4.6 Разрыв II рода - когда хотя бы один из односторонних пределов не существует.

Теорема 4.2 Если при нахождении пределов возникает неопределенность типа или , целесообразно применить правило Лопиталя:

,

если последний существует.

Правило можно применять неоднократно до устранения неопределенности.

Определение 4.7 Точки, в которых функция достигает минимальное или максимальное значение, называется точками экстремума.

Для того, чтобы в точке функция принимала экстремальное значение, должны выполняться два условия существования экстремума -необходимое и достаточное.

Теорема 4.3 Необходимое условие: или не существует. Такие точки называются критическими, точками, I рода.

Теорема 4.4 Достаточное условие:

а) Производная слева и справа от критической точки имеет разные знаки. При смене знака производной с «+» на«-») в. точке функция достигает максимума; с «-» на «+» - минимума.

б) Вторая производная . Точка будет точкой максимума, если , и точкой минимума, если /"(^о)>0.

в) Если условие б) не выполняется, то определяется первая производная, отличная от нуля . При этом точка будет точкой экстремума, если -четное, а именно: максимума при и минимума при. Если - нечетное, то экстремума в точке не существует.

При нахождении и на отрезке следует дополнительно рассмотреть значение функции и на границах отрезка.

Теорема 4.5 Функция возрастает на интервалах, для которых , и убывает, если .

Определение 4.8 График функции называется выпуклым (вогнутым) вверх на интервале , если он расположен ниже (выше) касательной, проведенной в любой точке этого интервала.

Определение 4.9 Точкой перегиба называется точка, отделяющая выпуклую часть графика функции от вогнутой или наоборот. В точке должны выполняться два условия перегиба - необходимое и достаточное.

Теорема 4.6 Необходимое условие: или не существует. В этом: случае точка называется критической точкой II рода.

Теорема4.7 Достаточное условие: слева и справа от точки имеет различные знаки.

Теорема 4.8 Функция выпукла на интервале, где и вогнута в обратном, случае.

Определение 4.10 Прямая называется асимптотой кривой , если расстояние точки кривой от прямой стремится к нулю при неограниченном удалении указанной точки от начала координат.

Различают 2 вида асимптот: вертикальные и наклонные.

Прямая является вертикальной асимптотой кривой , если .

Прямая является горизонтальной асимптотой кривой если существует предел или .

Прямая является наклонной асимптотой кривой , если существуют пределы

или

Построение графиков функций по характерным точкам может осуществляться в следующей последовательности:

1. Найти область определения функции.

2. Определить точки пересечения с осями координат.

3. Исследовать функцию на симметрию (четность, нечетность), периодичность.

4. Исследовать функцию на непрерывность. Классифицировать точки разрыва, если последние существуют.

5. Исследовать функцию на экстремум, определить интервалы возрастания и убывания.

6. Исследовать функцию на перегибы, определить интервалы выпуклости, вогнутости.

7. Найти асимптоты графика функции.

8. Построить график функции.

Задача 4.7 Исследовать на непрерывность функцию

Решение

Используя определение модуля, можно записать

При терпит разрыв. Вычислим односторонние пределы:

Так как функция в точке имеет конечные несовпадающие пределы, то эта точка является точкой неустранимого разрыва 1 рода.

Задача 4.8 Исследовать и построить по характерным точкам график функции .

Решение

1. Областью определения данной функции является множество вещественных чисел.

2. Так как при также, то график функции пересекает координатные оси в начале координат.

3. . Так как и , то функция не является ни четной, ни нечетной, а, следовательно, не имеет симметрии ни относительно начала координат, ни относительно оси . Экспоненциальная функция не является периодической функцией.

4. Указанная функция является непрерывной на всей числовой оси.

5. Найдем критические точки 1 рода.

Из условия найдем единственное решение . Так как при переходе через эту точку производная меняет знак с «+» на «-», то является точкой максимума.

Интервал возрастания функции: .

Интервал убывания функции: .

6. Критические точки II рода определяются по второй производной.

.

Из определяем критическую точку .

Так как при переходе через эту точку меняет знак с «-» на «+», то будет точкой перегиба. Ее координаты равны

Интервал выпуклости функции: .

Интервал вогнутости функции: .

7. Так как , то вертикальной асимптоты не существует.

Горизонтальные асимптоты найдем из условий:

,

.

Следовательно, при неограниченном возрастании ось является горизонтальной: асимптотой При неограниченном убывании таковой не будет.

Так как при есть горизонтальная асимптота, то наклонной здесь не будет. Для интервала определим угловой коэффициент наклонной асимптоты из условия

.

Следовательно, здесь нет и наклонной асимптоты.

8. Наносим на координатную плоскость характерные точки и строим график функции (рис.4.2).

Рис.4.2

77