Односторонние пределы функций
Отметим,
что в определениях предела функции
никаких условий на способ стремления
к
не накладывалось. В этой связи имеют
следующие основные понятия.
Определение
3.9.Если значения функции
стремятся к числу
по мере стремления
к
со стороны меньших значений, то число
называется левосторонним пределом
функции в точке
,
т. е.
Определение
3.9.Если значения функции
стремятся к числу
по мере стремления
к
со стороны больших значений, то число
называется правосторонним пределом
функции в точке
,т. е.
Задача
3.5.Определить левосторонний и
правосторонний пределы функции
при
.
Проанализируем
показатель степени функции
.
При этом имеют два варианта.
а)
Если
,
то
при этом
.
б)
Если
,то
при этом 
.
Тема 3.4. Замечательные пределы Первый замечательный предел.
Предел
при
Функция
четная,
график ее представлен на рис.
3.3.
Рис. 3.3
Очевидно,
что при
отличается
неопределенностью
.
Если
есть радианная мера угла, то
и
.
Задача 3.6.Найти пределы функций.
а)
Приведенная задача сводится к первому замечательному пределу. При этом, имеем.
.
б)
.
Как
и в предыдущем примере, здесь
неопределенность типа
раскрывается путем применения первого
замечательного предела.
.
Второй замечательный предел
Числовая
последовательность
при
возрастает, но остается ограниченной.
Всякая возрастающая, но ограниченная
последовательность имеет предел. Предел,
к которому стремится
,
при
впервые определил Непер, обозначается
он через
,
т.е.
.
Число
еявляется иррациональным, кроме
того, оно трансцендентно и равно
=2,71828.
Функция
имеет пределом число
не только при целочисленных значениях
,но и тогда, когда
стремится к бесконечности, пробегая
числовую прямую непрерывно. Чтобы
отметить это обстоятельство, заменяя
на
имеем:
или
Последнее соотношение и определяет выражение для второго замечательного предела. Такой предел, выраженный через бесконечно малые, имеет вид
Задача 3.7.Найти пределы
а)
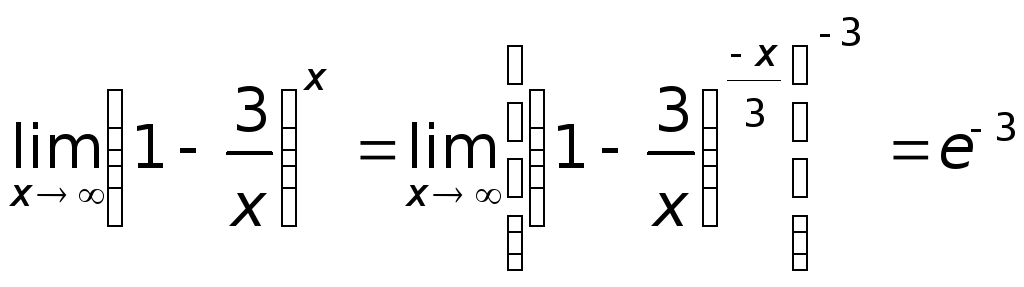
б)
Предел отношения многочленов при стремлении аргумента к бесконечности
Пусть
,
При
.
Тогда
Но
.
Следовательно,
Задача 3.8.Найти пределы
а)
.
б)
.