§ 34. Двойное векторное произведение

Пусть вектор а умножается векторно на вектор b, после чего получен­ный вектор [ab] умножается снова векторно на вектор с. В результате по­лучается так называемое двойное векторное произведение [[ab] с] (ясно, что [[ab] с] — вектор). Умножая вектор а векторно на [ab], получим двойное векторное произведение [a [[bс]].

Вообще говоря,

[[ab] с]  [a [bс]]

Докажем, что имеет место тождество

[[ab] с] = b(aс) — b(aс)

Доказательство. Введём (декартову прямоугольную) систему коор­динат. Чтобы облегчить выкладки, расположим оси координат специальным образом, а именно: ось Ох направим по вектору а, ось Оу поместим в плоскости векторов а и b (считая, что векторы а, b приведены к общему началу). В таком случае будем иметь:

a = {X₁; 0; 0}, b = {X₂; Y₂; 0}, с = {X₃; Y₃; Z₃},

Теперь находим:

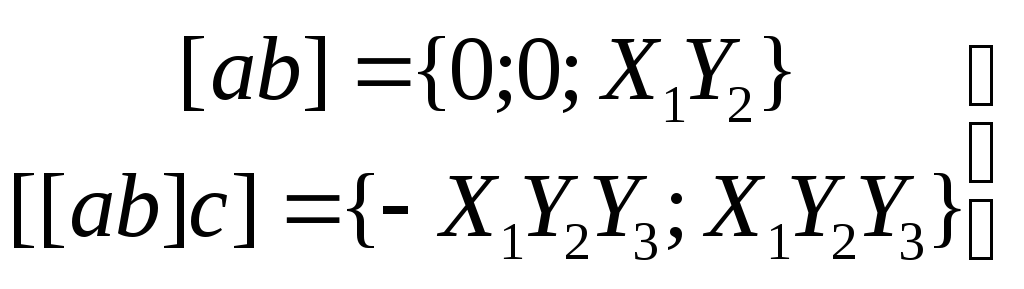
С другой стороны,

ас = Х₁Х₃; b(ас) = {Х₁Х₂Х,; Х₁X₂Х₃; 0},

bc = Х₂Х₃+ Y₂Y₃, a(bc) = {X₁X₂X₃ + X₁Y₂Y₃; 0; 0}.

Следовательно,

b (ас) — а (bс) = {— X₁X₂X₃; X₁Y₂Y₃; 0; }. (2)

Сравнивая правые части формул (1) и (2), получаем:

[[аb]с] = b(ас) — а(bс),

что и требовалось.

879. Доказать тождество

[a[bc]] = b(ac) — c(ab).

880. Решить задачу 864, используя тождества, данные в начале этого параграфа, и тождество задачи 879.

881. Даны вершины треугольника А(2; —1; —3), B(1; 2;—4) и С(3; —1; —2). Вычислить координаты вектора h, коллинеарного с его высотой, опущенной из вершины А на противоположную сторону, при условии, что вектор h образует с осью Оу тупой угол и что его модуль равен 2 .

882. Считая, что каждый из векторов а, b, с отличен от нуля, установить, при каком их взаимном расположении справедливо ра­венство

[a[bc]] = [[ab]c],

883. Доказать тождества:

1) [a[bc]] + [b] [ca] + [c[ab] = 0;

2) [ab] [cd] = (ас) (bd) — (ad) (bc);

3) [ab] [cd] + [ас] [db]+[ad] [bc] = 0;

4) [[ab] [cd]] = c(abd) — d(abc);

5) [ab] [bc] [ca] = (abc)²;

6) [а [а [а [ab]]]] = a⁴b при условии, что векторы а и b взаимно перпенди-кулярны;

7) [а (b [cd]]] = [ас] (bd) — [ad] (bc);

8) [a[b[cd]]] = (acd)b — (ab)[cd];

9) [аb]² [ас]² — ([ab] [ас]) = а² (аbс)²;

10) [[ab] [bc]} [[bс] [са]] [[са] [ab]] = (abc)⁴;

11) (аb) [cd] + (ас) \db] + (ad) [bc] = a (bcd);

12)

884. Три некомпланарных вектора a, b и с приведены к общему началу. Доказать, что плоскость, проходящая через концы этих векторов, перпендикулярна к вектору

[аb] + [bс] + [са

§ 36. Уравнение поверхности

Уравнением данной поверхности (в выбранной системе координат) на­зывается такое уравнение с тремя переменными

Р(х, у, z)=0,

которому удовлетворяют координаты каждой точки, лежащей на этой по­верхности, и не удовлетворяют координаты никакой точки, не лежащей на ней.

885. Даны точки М₁(2; —3; 6), М₂(0; 7; 0), М₃(3; 2; —4), М₄(2; 4; — 5),М₅(1; —4; —5), М₆(2; 6; — ). Установить, какие из них лежат на поверхности, определенной уравнениемх² + у² + 2² = 49, и какие не лежат на ней? Какая поверхность определена данным уравнением?

886. На поверхности х^а + у^а + r² = 9 найти точку, для кото­рой: 1) абсцисса равна 1, ордината равна 2; 2) абсцисса равна 2, ордината равна 5; 3) абсцисса равна 2, апликата равна 2; 4) орди­ната равна 2, апликата равна 4.

887. Установить, какие геометрические образы определяются следующими уравнениями в декартовых прямоугольных координатах пространства:

1) х = 0; 2) у = 0; 3) z = 0; 4) х —2 = 0;

5) y + 2 = 0; 6) z + 5 = 0; 7) х³ + у² + z² = 25;

8) (х — 2)² + (у + 3)² + (z — 5)² = 49;

9) х² + 2у² + 3z² = 0; 10) х² + 2у² + 3z² + 5 = 0;

11) х — у =0; 12) х + z = 0; 13) у — 2 = 0; 14) ху = 0;

15) хz = 0; 16) yz = 0; 17) хуz = 0; 18) х² —4х = 0;

19) ху — у^а = 0; 20) уz + z ² = 0.

888. Даны две точки F₁(—с; 0; 0) и F₂(c; 0; 0). Вывести урав­нение геометрического места точек, сумма расстояний которых до двух данных точек есть величина постоянная, равная 2а при усло­вии а>0, с>0; а>с.

Р е ш е н и е. Обозначим буквой М произвольную точку пространства, буквами х, у, z — её координаты. Так как точка М может занимать любое по­ложение, то х, у и z являются переменными величинами; их называют те­кущими координатами.

Точка М лежит на данной поверхности в том и только в том случае, когда

MF₁ + MF₂ = 2a. (1)

Это есть определение поверхности, выраженное символически. Выразим MF₁ и MF₂ — j через текущие координаты точки М:

MF₁ = , MF₂ = .

Подставим полученные выражения в равенство (1). Тем самым мы най­дём уравнение

(2)

которое связывает текущие координаты х, у, z. Это и есть уравнение дан­ной поверхности.

Действительно, для каждой точки М, лежащей на данной поверхности, выполняется условие (1) и, следовательно, координаты такой точки будут удовлетворять уравнению (2); для каждой точки, не лежащей на поверхности, условие (1) не будет выполняться и, следовательно, её координаты не будут удовлетворять уравнению (2). Таким образом, задача решена; дальнейшие выкладки имеют целью представить уравнение поверхности в более простом виде.

Уединим в уравнении (2) первый радикал:

возведём обе части этого равенства в квадрат и раскроем скобки; мы по­лучим:

x² + 2cx+с²+y² + z² =

= 4а² — 4а

или а

Снова, освобождаясь от радикала, найдём:

a²x² — 2a²cx + а²с² + a² y² + a² z² = a⁴ — 2а²сх + с²x²,

или

(а² — с²) х² + a²y² + a²2² = а² (а² — с²). (3)

Так как а > с, то а² — с² > 0; положительное число a² — с² обозначим через b². Тогда уравнение (3) примет вид

b²x² + а²y + a²z² = a²b³

или

Рассматриваемая поверхность называется эллипсоидом вращения. Урав­нение (4) называется каноническим уравнением этого эллипсоида.

889. Вывести уравнение сферы, центр которой находится в на­чале координат и радиус которой равен г.

890. Вывести уравнение сферы, центр которой С(α; β; γ) и ра­диус которой равен r.

891. Из точки Р(2; 6; —5) проведены всевозможные лучи до пересечения с плоскостью Oxz. Составить уравнение геометриче­ского места их середин.

892. Из точки А(3; —5; 7) проведены всевозможные лучи до пересечения с плоскостью Оху. Составить уравнение геометриче­ского места их середин.

893. Из точки С(—3; —5; 9) проведены всевозможные лучи до пересечения с плоскостью Oyz. Составить уравнение геометриче­ского места их середин.

894. Вывести уравнение геометрического места точек, раз­ность квадратов расстояний которых до точек F₁(2; 3;— 5) и F₂(2;— 7; —5) есть величина постоянная, равная 13.

895. Вывести уравнение геометрического места точек, сумма квадратов расстояний которых до двух точек F₁(— а; 0; 0) и F₂(а; 0; 0) равна постоянной величине 4а².

896. Вершины куба суть точки А(— а; — а; — а), В(а; —а; —а), С(—а; а; —а) и D(a; а; а). Составить уравнение геометрического места точек, сумма квадратов расстояний которых до граней этого куба есть величина постоянная, равная 8а².

897. Вывести уравнение геометрического места точек, равно­удалённых от двух точек М₁(1; 2; —3) и M₂(3; 2; 1).

898. Вывести уравнение геометрического места точек, сумма расстояний которых до двух данных точек F₁(0; 0; — 4) и F₂(0; 0; 4) есть величина постоянная, равная 10.

899. Вывести уравнение геометрического места точек, разность расстояний которых до двух данных точек F₁(0; — 5; 0) и F₂(0; 5; 0) есть величина постоянная, равная 6.