
- •§ 1. Ось и отрезки оси. Координаты на прямой
- •§ 2. Декартовы прямоугольные координаты на плоскости
- •§ 3. Полярные координаты
- •§ 4. Направленный отрезок. Проекция отрезка
- •На произвольную ось. Проекции отрезка на оси координат.
- •Длина и полярный угол отрезка. Расстояние
- •Между двумя точками
- •§ 5. Деление отрезка в данном отношении
- •§ 6. Площадь треугольника
- •§ 7. Преобразование координат
- •§ 8. Функция двух переменных
- •§ 9. Понятие уравнения линии. Задание линии при помощи уравнения
- •§ 10. Вывод уравнений заранее данных линий
- •§ 11. Параметрические уравнения линии
- •§ 12. Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых
- •§ 13. Неполные уравнения прямой. Совместное исследование уравнений двух и трёх прямых. Уравнение прямой «в отрезках»
- •§ 14. Нормальное уравнение прямой. Задача определения расстояния от точки до прямой
- •§ 15. Уравнение пучка прямых
- •§ 16. Полярное уравнение прямой
- •§ 17. Окружность
- •§ 18. Эллипс
- •§ 19. Гипербола
- •§ 20. Парабола
- •§ 21. Полярное уравнение эллипса, гиперболы и параболы
- •§ 22. Диаметры линий второго порядка
- •§ 23. Центр линии второго порядка
- •§ 24. Приведение к простейшему виду уравнения центральной линии второго порядка
- •§ 25. Приведение к простейшему виду параболического уравнения
- •§ 26. Уравнения некоторых кривых, встречающихся в математике и её приложениях
- •§ 27. Декартовы прямоугольные координаты в пространстве
- •§ 28. Расстояние между двумя точками. Деление отрезка в данном отношении
- •§ 29. Понятие вектора. Проекции вектора
- •§ 30. Линейные операции над векторами
- •§ 31. Скалярное произведение векторов
- •§ 32. Векторное произведение векторов
- •§ 33. Смешанное произведение трёх векторов
- •§ 34. Двойное векторное произведение
- •§ 36. Уравнение поверхности
- •§ 36. Уравнения линии. Задача о пересечении трёх поверхностей.
- •§ 37. Уравнение цилиндрической поверхности с образующими, параллельными одной из координатных осей
- •§ 38. Общее уравнение плоскости. Уравнение плоскости, проходящей через данную точку и имеющей данный нормальный вектор
- •§ 39. Неполные уравнения плоскостей. Уравнение плоскости «в отрезках»
- •40. Нормальное уравнение плоскости. Расстояние от точки до плоскости.
- •§ 41. Уравнения прямой
- •§ 42. Направляющий вектор прямой. Канонические уравнения прямой. Параметрические уравнения прямой
- •§ 43. Смешанные задачи, относящиеся к уравнению плоскости и уравнениям прямой
- •§ 44. Сфера
- •§ 45. Уравнения плоскости, прямой и сферы в векторной символике
- •§ 46. Поверхности второго порядка.
§ 21. Полярное уравнение эллипса, гиперболы и параболы
Полярное уравнение, общее по форме для эллипса, одной ветви гиперболы и параболы имеет вид
![]() ,
(1)
,
(1)
где , — полярные координаты произвольной точки линии, р — фокальный параметр (половина фокальной хорды линии, перпендикулярной к её оси), — эксцентриситет (в случае параболы = 1). Полярная система координат при этом выбрана так, что полюс находится в фокусе, а полярная ось направлена по оси линии в сторону, противоположную ближайшей к этому фокусу директрисы.
628. Дано
уравнение эллипса
![]() =
1. Составить его полярное уравнение,
считая, что направление полярной оси
совпадает с положительным направлением
оси абсцисс, а полюс находится:
=
1. Составить его полярное уравнение,
считая, что направление полярной оси
совпадает с положительным направлением
оси абсцисс, а полюс находится:
1) в левом фокусе эллипса; 2) в правом фокусе.
629. Дано
уравнение гиперболы
![]() =
1. Составить полярное уравнение её
правой ветви, считая, что направление
полярной оси совпадает с положительным
направлением оси абсцисс, а полюс
находится:
=
1. Составить полярное уравнение её
правой ветви, считая, что направление
полярной оси совпадает с положительным
направлением оси абсцисс, а полюс
находится:
1) в правом фокусе гиперболы; 2) в левом фокусе.
630. Дано
уравнение гиперболы
![]() =
1. Составить полярное уравнение её
левой ветви, считая, что направление
полярной оси совпадает с положительным
направлением оси абсцисс, а полюс
находится:
=
1. Составить полярное уравнение её
левой ветви, считая, что направление
полярной оси совпадает с положительным
направлением оси абсцисс, а полюс
находится:
1) в левом фокусе гиперболы; 2) в правом фокусе.
631. Дано уравнение параболы у2 = 6х. Составить её полярное уравнение, считая, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится в фокусе параболы.
632. Определить, какие линии даны следующими уравнениями в полярных координатах:
1)
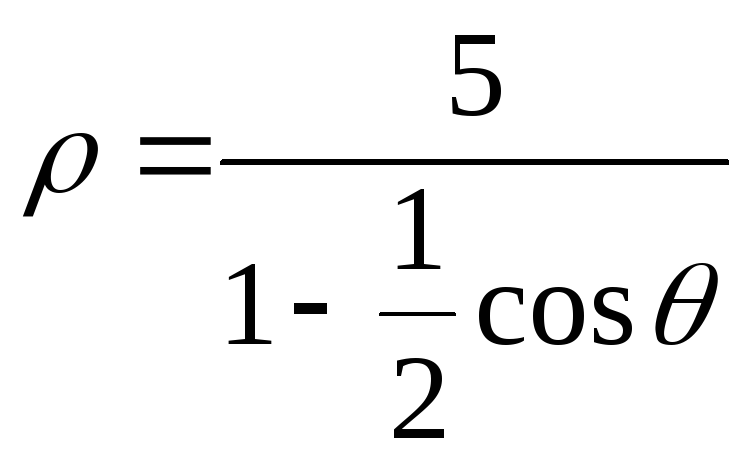 ,
2)
,
2)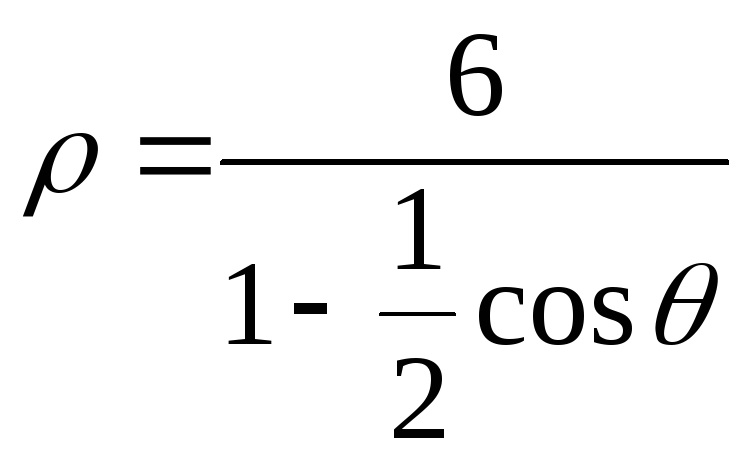 , 3)
, 3)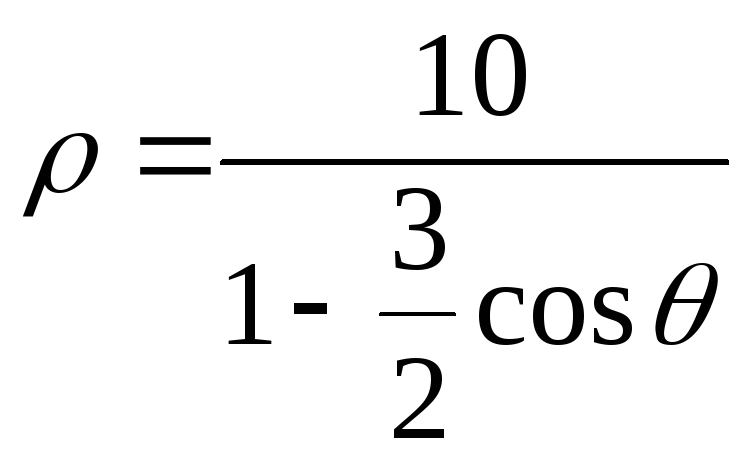 ,
,
4)
![]() ,
5)
,
5)![]() , 6)
, 6)![]() ,
,
633.
Установить, что уравнение 1)
![]() ,
определяет эллипс, и найти его полуоси.
,
определяет эллипс, и найти его полуоси.
634.
Установить, что уравнение
![]() определяет правую ветвь гиперболы
и найти ей полуоси.
определяет правую ветвь гиперболы
и найти ей полуоси.
635.
Установить, что
уравнение
![]() определяет
эллипс, и составить полярные уравнения
его директрис.
определяет
эллипс, и составить полярные уравнения
его директрис.
636.
Установить, что уравнение
![]() определяет
правую ветвь гиперболы, и составить
полярные уравнения директрис и асимптот
этой гиперболы.
определяет
правую ветвь гиперболы, и составить
полярные уравнения директрис и асимптот
этой гиперболы.
637. На
эллипсе
![]() найти точки, полярный
радиус которых равен 6.
найти точки, полярный
радиус которых равен 6.
638. На
гиперболе
![]() найти
точки, полярный радиус которых равен
3.
найти
точки, полярный радиус которых равен
3.
639. На
параболе
![]() найти точки:
найти точки:
1) с наименьшим полярным
радиусом; 2) с полярным радиусом, равным
параметру параболы.![]()
640. Дано
уравнение эллипса
![]() Составить его полярное уравнение
при условии, что направление полярной
оси совпадает с положительным направлением
оси абсцисс, а полюс находится в центре
эллипса.
Составить его полярное уравнение
при условии, что направление полярной
оси совпадает с положительным направлением
оси абсцисс, а полюс находится в центре
эллипса.
641. Дано
уравнение гиперболы
![]() .Составить
её полярное уравнение при условии,
что направление полярной оси совпадает
с положительным направлением оси
абсцисс, а полюс находится в центре
гиперболы.
.Составить
её полярное уравнение при условии,
что направление полярной оси совпадает
с положительным направлением оси
абсцисс, а полюс находится в центре
гиперболы.
642. Дано уравнение параболы у2 = 2рх. Составить её полярное уравнение при условии, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится в вершине параболы.
§ 22. Диаметры линий второго порядка
В курсе аналитической геометрии доказывается, что середины параллельных хорд линии второго порядка лежат на одной прямой. Эта прямая называется диаметром линии второго порядка. Диаметр, делящий пополам какую-нибудь хорду (а значит, и все параллельные ей), называется сопряжённым этой хорде (и всем хордам, которые ей параллельны). Все диаметры эллипса и гиперболы проходят через центр. Если эллипс задан уравнением
![]() ,
(1)
,
(1)
то его диаметр, сопряжённый хордам с угловым коэффициентом k, определяется уравнением
![]() .
.
Если
гипербола задана уравнением
![]() ,
(2)
,
(2)
то её диаметр, сопряжённый
хордам с угловым коэффициентом k,
определяется уравнением
![]() .Все диаметры параболы
параллельны её оси. Если парабола задана
уравнением y2
= 2px
то её диаметр,
сопряжённый хордам с угловым коэффициентом
k,
определяется уравнением
.Все диаметры параболы
параллельны её оси. Если парабола задана
уравнением y2
= 2px
то её диаметр,
сопряжённый хордам с угловым коэффициентом
k,
определяется уравнением
![]() .
.
Если один из двух диаметров эллипса или гиперболы делит пополам хорды, параллельные другому, то второй диаметр делит пополам хорды, параллельные первому. Такие два диаметра называются взаимно сопряжёнными.
Если k
и k'
— угловые коэффициенты
двух взаимно сопряжённых диаметров
эллипса (1), то
![]() (3)
(3)
Если k и k' — угловые коэффициенты двух взаимно сопряжённых диаметров гиперболы (2), то
![]() (4)
(4)
Соотношения (3) и (4) называются условиями сопряжённости диаметров соответственно для эллипса и для гиперболы. Диаметр линии второго порядка, перпендикулярный к сопряжённым хордам, называется главным.
643.
Составить уравнение диаметра эллипса
![]() ,
проходящего через
середину его хорды, отсекаемой на прямой
2х — у
— 3 = 0.
,
проходящего через
середину его хорды, отсекаемой на прямой
2х — у
— 3 = 0.
644.
Составить уравнение хорды эллипса
![]() ,
проходящей
через точку А
(1; —2) и делящейся ею пополам.
,
проходящей
через точку А
(1; —2) и делящейся ею пополам.
645. Составить уравнения двух взаимно сопряжённых диаметров эллипса х2 + 4у2 = 1, из которых один образует с осью Ох угол в 45°.
646. Составить уравнения двух взаимно сопряжённых диаметров эллипса 4х2 + 9у2 = 1, из которых один параллелен прямой х + 2у —5 = 0.
647. Составить уравнения двух взаимно сопряжённых диаметров эллипса х2 + 3у2 = 1, из которых один перпендикулярен к прямой 3х + 2у — 7 = 0.
648.На чертеже изображён эллипс. Пользуясь циркулем и линейкой, построить его центр.
649.Доказать, что оси эллипса являются единственной парой его главных диаметров.
650. Пользуясь свойствами сопряжённых диаметров, доказать, что каждый диаметр окружности является главным.
651. а) В эллипс вписан равнобедренный треугольник так, что одна его вершина совпадает с одной из вершин эллипса. Доказать, что основание этого треугольника параллельно одной из осей эллипса.
б) Доказать, что стороны прямоугольника, вписанного в эллипс, параллельны осям этого эллипса.
в) На чертеже изображён эллипс. Пользуясь циркулем и линейкой, построить его главные диаметры.
652.Доказать, что хорды эллипса, соединяющие его произвольную точку с концами любого диаметра этого эллипса, параллельны паре его сопряжённых диаметров.
653. а) Доказать, что сумма квадратов двух сопряжённых полудиаметров эллипса есть величина постоянная (равная сумме квадратов его полуосей).
б) Доказать, что площадь параллелограмма, построенного на двух сопряжённых полудиаметрах эллипса, есть величина постоянная (равная площади прямоугольника, построенного на его полуосях).
654.
Составить уравнение диаметра гиперболы
![]() ,
проходящего через середину её хорды,
отсекаемой на прямой 2х
— y + 3
= 0.
,
проходящего через середину её хорды,
отсекаемой на прямой 2х
— y + 3
= 0.
655. Дана
гипербола
![]() .
Составить уравнение
её хорды,
.
Составить уравнение
её хорды,
которая проходит через точку А(3; —1) и делится точкой А пополам.
656. Составить уравнения двух сопряжённых диаметров гиперболы х2— 4у2 = 4, из которых один проходит через точку А (8; 1).
657.Составить уравнения сопряжённых диаметров гиперболы
![]() ,
угол между которыми равен 45°.
,
угол между которыми равен 45°.
658.На чертеже изображена гипербола. Пользуясь циркулем и линейкой, построить её центр.
659.Доказать, что оси гиперболы являются единственной парой её главных диаметров.
660.На чертеже изображена гипербола. Пользуясь циркулем и линейкой, построить её главные диаметры.
661. Составить уравнение диаметра параболы у2 = 12х, проходящего через середину её хорды, отсекаемой на прямой 3х + y — 5 = 0.
662. Дана парабола у2 = 20х. Составить уравнение её хорды, которая проходит через точку А(2; 5) и делится точкой А пополам.
663.Доказать, что ось параболы является единственным её главным диаметром.
664.На чертеже изображена парабола. Пользуясь циркулем и линейкой, построить её главный диаметр.
