Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет пищевых технологий

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

matra.rozpaxyhk.pdf

Скачиваний:

Добавлен:

12.02.2016

Размер:

761.1 Кб

Скачать

☆

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

3.Елементи аналітичної геометрії [1, c. 76 - 83, 97 - 113], [2, c. 26 - 43].

3.1.Пряма лінія на площині.

Розглянемо окремі види рівнянь прямих ліній на площині:

1) Рівняння прямої з кутовим коефіцієнтом.

Рівняння прямої має вигляд: y = kx + b ,

де k = tgj – кутовий коефіцієнт прямої, j –кут утворений прямою і додатним напрямом осі Ох, а b – ордината точки перетину прямої з віссю Оy.

2) Загальне рівняння прямої.

Вектор n = (A; B), який перпендикулярний до прямої, називають нормальним вектором прямої або вектором нормалі. Будемо вважати відомими координати точки M 0 (x0 ; y0 ), що лежить на прямій, а M (x; y) – довільна точка прямої.

Рівняння вигляду:

A(x - x0 )+ B(y - y0 )= 0

визначає пряму, що проходить через задану точку M 0 (x0 , y0 ) із заданим

нормальним вектором n = (A; B). Останнє рівняння можна переписати у вигляді:

Ax + By + C = 0,

яке називають загальним рівнянням прямої. Тут C = -Ax0 - By0 .

Кутовий коеффіцієнт k прямої визначається так: k = - A .

Коефіцієнти A і B є координатами нормального вектора до прямої, а тому вони дозволяють одержати уявлення про її розташування на площині.

Якщо A = 0 , B ¹ 0 , то рівняння такої прямої має вигляд: By + C = 0 – пряма паралельна осі абсцис. При C = 0 пряма y = 0 визначає вісь Ox .

Якщо A ¹ 0 , B = 0 , то рівняння прямої набуває вигляду: Ax + C = 0. Дана пряма паралельна осі ординат. При C = 0 рівняння x = 0 є рівнянням вісі Oy .

Якщо C = 0 , то Ax + By = 0 . Рівнянню задовольняє точка О(0,0) і пряма проходить через початок координат.

3) Рівняння прямої, яка проходить через задану точку і має заданий кутовий коефіцієнт.

Нехай пряма проходить через точку M 0 (x0 ; y0 ) і її напрям задається кутовим коефіцієнтом k . Рівняння цієї прямої має вигляд:

y- y0 = k(x - x0 ).

4)Рівняння прямої, яка проходить через дві задані точки.

Нехай	пряма проходить через точкиM (x ; y ) і			M	2	(x	; y	2	), тоді
y2 - y1 = k(x2	1	1	1		2	2		2
y2 - y1 = k(x2	- x1 ) або

k = y2 - y1 . x2 - x1

Підставимо значення k в рівняння y - y1 = k(x - x1 ) та отримаємо:

x - x1 = y - y1 x2 - x1 y2 - y1

– рівняння прямої, яка проходить через дві задані точки.

5) Рівняння прямої у відрізках на осях.

x - a y - 0

Пряма проходить через точки M 1 (а;0) і M 2 (0;b), тоді : 0 - a = b - 0 , x + y =1– рівняння прямої у відрізках на осях.

6)Канонічне рівняння прямої.

Нехай пряма проходить через задану точку M 0 (x0 ; y0 ) і задано ненульовий

® ®

вектор s = (m;n ,)який паралельний до прямої. Вектор s називають напрямним вектором прямої. В цьому випадку рівняння прямої має вигляд:

x - x0 = y - y0 – канонічне рівняння прямої.

3.2.Кут між двома прямими, умови паралельності і перпендикуляр-

ності двох прямих на площині.

Нехай прямі L1 і L2 задані рівняннями з кутовими коефіцієнтами

y = k

x + b

і y = k

x + b , де k

= tga

, k

= tga

, a

= ç L , Ox ÷

= ç L , Ox ÷ .

Тоді tgj = tg(a

tga2 - tga1

k2 - k1

- a

, j = ç L , L

÷ .

+ tga1 tga2

+ k1k2

Звідси tgj = k2 - k1 . 1 + k1k2

Якщо необхідно визначити гострий кут між прямими, формула набуває

вигляду: tgj = k2 - k1 . 1 + k1k2

Якщо

L || L , то

j = 0, tgj = 0 ,

- k1

= 0 ,

- k

= 0 . Отже, рівність

1 + k1k2

k1 = k2 –умова паралельності прямих.

При L

^ L

, j =

, ctgj = 0 ,

1 + k1k2

= 0 , 1 + k

= 0 . Таким чином, умо-

k2 - k1

ва перпендикулярності прямих має вигляд k1k2 = -1.

Приклад. Скласти рівняння прямої, якщо вона задається точкою

M 0 (1;-2) та вектором нормалі n = (- 4;2). Побудувати пряму.

Розв`язання.

Підставимо значення M 0 (x0 ; y0 )= M 0 (1;-2) та n = (A; B)= (- 4;2) в рівнян-

ня A(x - x0 )+ B(y - y0 )= 0 : - 4 × (x -1)+ 2 × (y - (- 2))= 0 , - 4x + 2 y + 8 = 0 .
Отже, 2x - y - 4 = 0 – рівняння шуканої прямої.
Для побудови прямої на площині достатньо двох точок . Одна точка
M 0 (1;-2) задана, а координати другої точки M1 (x1 ; y1 ) знайдемо так: нехай
x1 = 0 , тоді 2 × 0 - y1 - 4 = 0, y1 = -4 . Отже, M 1 (0;-4). Пряму зображено на рис 2.
Рис.2.					Рис. 3.
Приклад. Скласти рівняння прямої, що вона задається точкою M 0 (- 3;3)
®
та напрямним вектором s = (2;-1). Побудувати пряму.
Розв`язання. x - x0	= y - y0 . Враховуючи, що x0 = -3 , y0 = 3, m = 2 ,
m	n
n = -1, одержимо: x - (- 3) = y - 3 , -(x +3)= 2(y -3), x + 2 y -3 = 0. Рівнянню
2	-1
прямої (рис.3.) задовольняють точки M 0 (- 3;3), M 1 (3;0).
Приклад. Скласти рівняння прямої, що проходить через задану точку
M 0 (4;-1) і має кутовий коефіцієнт k = - 1 . Побудувати пряму.
		2			k = - 1 в рівняння
Розв`язання. Підставимо x = 4 ,		y	0	= -1,	k = - 1 в рівняння
	0		0		2
					2
y - y0 = k(x - x0 ). Отже,	y - (-1 )= - 1 (x - 4), 2 y + 2 = -х + 4 , x + 2 y - 2 = 0 . Для
	2
побудови прямої (рис.4.) використаємо точки M 0 (4;-1) і M 1 (2;0).
Рис.4.					Рис. 5.
		13

Приклад. Скласти рівняння прямої, що проходить через дві задані точки M 1 (-1;2) і M 2 (2;1). Побудувати пряму.

Розв`язання. Виходячи із рівняння

x - x1

y - y1

та враховуючи, що

x2 - x1

y2 - y1

x1 = -1, y1 = 2 , x2 = 2 ,

y2 =1, одержимо:

x - (-1)

y - 2

x +1

y - 2

, 3(y - 2)= -(x +1), x + 3y - 5 = 0 .

1 - 2

2 - (-1 )

-1

Для побудови прямої (рис.5.) використаємо точки M 1 (-1;2) і M 2 (2;1).

Приклад. Скласти рівняння прямої, що відтинає на осях Ох і Оу відповідно відрізки a = -4 і b = 3. Побудувати пряму.

Розв`язання. Використаємо рівняння у відрізках на осях x + y =1, a b

x+ y =1. Помножимо останнє рівняння на –12, тоді 3x - 4 y +12 = 0 . Для по-

-4 3

будови прямої (рис.6.) маємо точки

Рис. 6.

M 0 (- 4;0) і M 1 (0;3).

Рис. 7.

Приклад. У трикутнику, заданому вершинами A(- 2;3), B(5;1) і C(7;5) знайти:

1)рівняння і довжину медіани AM , проведеної з вершини A ;

2)рівняння висоти AN , проведеної з вершини A ;

3)рівняння прямої L , що проходить через вершину A паралельно стороні BC ;

4)побудувати у декартовій прямокутній системі координат трикутник ABC , відрізки AM , AN та пряму L .

Розв`язання. 1) За умовою AM – медіана, тому точка M ділить сторону

BC навпіл, та xM =

xB + xC

5 + 7

= 6 , yM

yB + yC

1 + 5

= 3, M (6;3).

Далі використаємо рівняння

x - xM

y - yM

прямої, що проходить че-

yA - yM

xA - xM

рез дві задані точки M (6;3) і A(- 2;3). Маємо

x - 6

y - 3

x - 6

y - 3

- 2 - 6

- 8

3 - 3

0 × (x - 6)= -8(y - 3). Отже y - 3 = 0 – рівняння медіани AM . Довжина об-

AM =

числюється за формулою:

(xM - xA )2 + y(M - yA )2

AM = 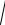(6 - (- 2))2 + (3 - 3)2 = 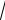82 = 8 .

2) За умовою задачі AN ^ BC , тому kBC × kAN = -1. Знайдемо

kBC

- yC

, потім k AN

= -

і використаємо рівняння y - yA = kAN (x - xA ).

kBC

xB - xC

Отже, kBC =

1 - 5

- 4

= 2 , k AN = -

, A(- 2;3), y - 3 = -

(x + 2),

- 2

5 - 7

2 y - 6 = -(x + 2), x + 2 y - 4 = 0 – рівняння висоти AN , проведеної з вершини A .

L || BC ,

тому

= kBC , тобто

kL = 2 . Далі

використаємо

y - yA = kL (x - xA ),

y - 3 = 2(x + 2), 2x - y + 7 = 0 – рівняння прямої L , що про-

ходить через вершину A паралельно стороні BC . Трикутник ABC зображено на рис. 7.

3.3. Криві другого порядку.

Нехай задано загальне рівняння другого степеня, яке не містить добутки змінних x і y : Ax2 + By 2 + Cx + Dy + E = 0.

Дане рівняння визначає: або коло при	A = B ¹ 0 , або еліпс при A × B > 0 ,
або гіперболу приA × B < 0 , або	параболу приA = 0, B ¹ 0 (або

B = 0, A ¹ 0 ). При цьому можливі випадки виродження: для еліпса (кола) – в точку або уявний еліпс (коло), для гіперболи – в пару прямих, що перетинаються, для параболи – в пару паралельних прямих.

Методом виділення повних квадратів відносно кожної змінної рівняння

Ax2 + By 2 + Cx + Dy + E = 0 можна привести до вигляду:

(x - x0 )2

+ (y - y0 )2

= R2

рівняння кола радіуса R з

центром

точці

C(x0 ; y0 ).

(x - x0 )2

+ (y - y0 )2

=1 – рівняння еліпса з центром у точціC(x

; y

) і

півосями a і b.

(x - x0 )2

- (y - y0 )2

= ±1

– рівняння гіперболи

центром

точці

C(x0 ; y0 ) і півосями a і b.

(y - y0 )2

= ±2 p(x - x0 ) або (x - x0 )2 = ±2 p( y - y0 )

– рівняння параболи

з вершиною в точці C(x0 ; y0 ), симетричної відносно прямої y = y0 або x = x0 .

Якщо у наведених рівняннях покласти x0 = y0

= 0 , то одержимо канонічні

рівняння відповідних кривих.

Приклад. Встановити тип кривої 25x2 + 9 y 2

+100x -18 y -116 = 0 та по-

будувати її.

Розв’язання. За умовою A = 25, B = 25, A × B > 0 , то рівняння описує еліпс. Далі виділимо повний квадрат відносно змінної х та змінної у:

25(x2 + 4x) + 9( y2 - 2 y) -116 = 0 ;

25(x2 + 2 × 2 × x + 4 - 4) + 9( y2 - 2 ×1× y +1 -1) -116 = 0 ;
25(x + 2)2		-100 + 9( y -1)2 - 9 -116 = 0 ; 25(x + 2)2 + 9( y -1)2 = 225 ;
(x + 2)2	+ (y -1)2		=1. Одержали рівняння еліпса з центром у точці С(–2;1)
9		25
та півосями а=3 та b= 5 (рис. 8.).
Приклад.		Встановити тип кривої 9x2 -16 y 2 + 36x +160 y - 508 = 0			та по-
будувати її.
Розв’язання. A = 9, B = -16, A × B < 0 , тому маємо гіперболу.
Виділимо повний квадрат:
9(x2 + 4x + 4 - 4) -16( y 2				-10 y + 25 - 25) - 508 = 0 ;
9(x + 2)2 - 36 -16( y - 5)2				+ 400 - 508 = 0 ; 9(x + 2)2 -16( y - 5)2 =144 ;
(x + 2)2	- (y - 5)2		=1. Одержали рівняння гіперболи з центром у точці С(–
16		9
2;5) та півосями а=4 та b= 3 (рис. 9.).
Рис. 8.				Рис. 9.

Приклад. Встановити тип кривої y2 + 10 y - 4x + 9 = 0 та побудувати її.

Розв’язання. A = 0, B =1– парабола.

y2 + 10 y + 25 - 25 - 4x + 9 = 0 , (y + 5)2 = 4x +16 , (y + 5)2 = 4(x + 4). Одер-

жали рівняння параболи з вершиною у точці С(–4;–5). Знайдемо точки перетину параболою вісі Ox і Oy :

Ox : y = 0 , - 4x + 9 = 0 , x = 9 ;

Oy : x = 0 , y2 +10 y + 9 = 0 , x1 = -1, x2 = -9 .

Парабола зображена на рис.10.

Рис. 10.

Запитання до самоконтролю

1.Дайте означення рівняння лінії на площині.

2.Запишіть рівняння прямої з кутовим коефіцієнтом. Який геометричний зміст у ньому мають коефіцієнти k і b ?

3.Запишіть рівняння прямої, що проходить через дві дані точки. Як можна визначити k ?

4.Загальне рівняння прямої. Які координати має нормальний вектор цієї

прямої?

5.Канонічне рівняння прямої.

6.Запишіть формулу обчислення кута між двома прямими, якщо їх задано рівняннями з кутовими коефіцієнтами. Як виражаються умови паралельності, перпендикулярності цих прямих?

7.Навести канонічні рівняння кола, еліпса, гіперболи і параболи.

4.Вступ до математичного аналізу [1, c.131 - 190], [2, c. 44 - 64]

Число A називається границею функції f (x) в точці x0 , якщо для будь-

якого числа e > 0 існує таке число d(e) > 0 , що для всіх значень x ¹ x0 ,					які за-
довольняють нерівність	x - x0	< d , має місце нерівність	f (x)- A	< e .	Якщо

число A є границею функції f (x) при x , що прямує до x0 , то цей факт симво-

лічно записується так: lim f (x)= A .

x®x 0

Наведемо основні теоретичні відомості:
1) Функція	f (x)	називається	нескінченно	малою приx ® x0 , якщо
lim f (x) = 0 .
x®x0	f (x) називається нескінченно великою при x ® x0 , якщо має
2) Функція	f (x) називається нескінченно великою при x ® x0 , якщо має
місце одна із рівностей:		lim f (x) = ¥ ,	lim f (x) = +¥ ,	lim f (x) = -¥ .
		x®x0	x®x0	x®x0
3) Функція	f (x) називається обмеженою при x ® x0 , якщо існує таке число

M > 0 та окіл точки x0 , такий, що f (x) £ M для всіх значень x із цього околу.

4.1. Властивості нескінченно малих функцій.

Якщо функція f (x)

нескінченно мала при x ® x0 , то і – f (x)

також

нескінченно мала при x ® x0 .

Якщо функції f1 (x)

f2 (x) нескінченно малі при x ® x0 , то їхні сума

та різниця f1 (x) + f2 (x) і

f1 (x) - f2 (x) також нескінченно малі при x ® x0 .

3) Якщо при x ® x0

функція f (x)

нескінченно мала, а функція g (x) —

обмежена, то їхній добуток f (x) g (x) і частка

f (x)

є також нескінченно мали-

g(x )

ми функціями при x ® x0 .

4.2. Властивості нескінченно великих функцій:

Якщо при x ® x0

функція f (x)

має скінчену границю (lim f (x)= A) , а

x®x0

функція g (x) – нескінченно велика ç lim g (x )= ¥÷, то:

è x®x0

f (x)

lim

(

+ g x

¥,

=lim

= 0.

)

( ) )

x®x0

g (x )

x®x0

Якщо lim f (x)= A,(A > 0),

lim g(x)= 0 , причому g (x)

додатна в деяко-

x®x0

f (x)

x®x0

му околі точки x , то lim

= +¥.

x®x0

g (x )

Якщо lim f (x) = +¥ і k > 0 , то lim (kf (x)) = +¥ .

x®x0

Якщо lim f (x) = ¥ і lim g (x) = ¥ , то lim ( f (x)g (x)) = ¥ .

x®x0

ями.

4.3. Зв'язок між нескінченно малими і нескінченно великими функці-

Якщо f (x) при x ® x0

– нескінченно велика функція, то функція

нескінченно мала.

f (x )

Якщо при x ® x0

функція g (x) – нескінченно мала, то функція

–

(x )

нескінченно велика, за умови, що в деякому околі точкиx0

функція g (x) не

перетворюється на нуль.

При обчисленні границь функцій використовують такі формули при умо-

ві, що означені в них границі існують і скінченні:

lim C = C , де C = const ;

2) lim ( f (x) ± g (x)) lim= f (x) ± lim g (x),

x®x0

lim ( f (x)× g (x))

lim= f (x)× lim g (x ), 4) lim C × f (x) = C lim f (x );

x®x0

5) lim

x®x0

f (x ) g (x )=

lim f (x)

x®x0		, де
lim g (x )
x®x0

		g(x )	æ		lim g(x)
lim g (x) ¹ 0 ;6)	lim ( f (x ))	g(x )	æ	öx®x
lim g (x) ¹ 0 ;6)	lim ( f (x ))		= ç lim	f (x )÷	0 .
x®x0	x®x0		è x®x0	ø

В усіх формулах не виключається можливість, що x0 = ¥ .

При обчисленні границь, які містять тригонометричні та обернені тригонометричні функції, використовують першу важливу границю:

lim sin x = 1.

x®0

Наслідками першої важливої границі є такі границі:

lim

sin (a x)

= lim

tg (a x)

=a , lim

arcsin(a x)

=a , lim

arctg(a x)

=a .

x®0

Якщо a(x)

та b (x)

нескінченно малі при x ® x0

та lim

a(х)

=1, то

x®x0 b (х )

a і b називаються еквівалентними нескінченно малими величинами. Еквівалентність нескінченно малих величин a і b позначається: a ~ b .

Наведемо ряд еквівалентностей, які використовуються при знаходженні границь, за умови, що функція a(x) – нескінченно мала:

1.sin a(x) ~ a(x) ;

2.tga(x) ~ a(x) ;

3.arcsina(x) ~ a(x) ;

4.arctga(x) ~ a(x) ;

5.1 - cosa(x) ~ a 2 (x) ;

6.aa( x) - 1 ~ a(x) ln a ;

7.ea (x) -1 ~ a(x) ;

8.ln(1 + a(x)) ~ a(x) ;

9 log a (1 + a(x)) ~ a(x) ln a ; 10. (1 + a(x))l -1 ~ l ×a(x) .

Зокрема, при l =	1	еквівалентність 10 набуває вигляду:			- 1 ~	a(x)	.
				1 + a(x)

2			2
При знаходженні границі відношення двох			нескінченно малих -ве

личин можна кожну (або тільки одну) з них замінювати іншою нескінченно малою величиною, їй еквівалентною, тобто якщо a ~a1 і b ~ b1, то

lim	a	= lim	a1	= lim	a	= lim	a1	.

x®а b		x®а b		x®а b		x®а b
				1		1

4.4. Обчислення границь.

Якщо f (x) є функцією елементарною, то при x ® a (точка a – належить області визначення функції) обчислення границі функції зводиться до простої підстановки значення x = a у функцію f (x) , тобто

lim f (x) = f (a).

x®a

Приклад. Знайти границю функції lim (x3 - 5x 2 + 2x + 4).

x®-3

Розв’язання. Задана функція є елементарною, вона визначена в точці

х = -3 , тому знаходимо границю функції як значення функції в точціх = -3 :

lim (x3 - 5x 2 + 2x + 4) = f (-3) = (-3)3 - 5 × (-3) 2 + 2 × (-3) + 4 = -74.

x®-3

Приклад. Знайти lim

- 3x + 5

x®-1

Розв’язання. lim

- 3x + 5

(-1)2

- 3

×(-1) + 5

1 + 3 + 5 9

x + 4

x®-1

-1 + 4

Якщо x прямує до нескінченності або до числа, що не належить області

визначення f (x) , то для

знаходження

границі необхідно

провести спеціальне

дослідження, яке називають розкриттям невизначеностей. Розглянемо розкриття деяких невизначеностей:

ì¥ü

1) Невизначеність виду í ý , якщо вона задана відношенням двох мно-

î¥þ

гочленів.

ì¥ü

Правило: для розкриття невизначеності í ý , заданої відношенням двох

î¥þ

многочленів, потрібно поділити чисельник і знаменник на старший степінь x у цих многочленах і перейти до границі.

Приклад. Знайти границю lim

3x4 - 5x2 +1

+ 7x4

Розв’язання.

x®¥ 2x - 4x3

3x4 - 5x2 +1

ì¥

3 -

3 - 0 + 0

lim

= í

lim=

2 4

0 - 0 + 7

x®¥ 2x - 4x3 + 7x4

î¥

þ x®¥ 2x - 4x3

+ 7x4

x®¥

+ 7

ì0ü

2) Невизначеність виду í ý, якщо вона задана відношенням двох мно-

î0þ

гочленів.

ì0ü

Правило: для розкриття невизначеності í ý, заданої відношенням двох

î0þ

многочленів, потрібно розкласти чисельник і знаменник на множники, скоротити на критичний множник (множник, через який чисельник і знаменник прямує до нуля) і перейти до границі.

Приклад. Знайти границю lim	2x2	-11x + 5	.

		-14x - 5
x®5 3x2

Розв’язання. Маємо відношення двох многочленів. Безпосередньою підстановкою переконуємося, що чисельник і знаменник відношення є нескінченно малі величини. Щоб виділити критичний множник необхідно чисельник і знаменник відношення розкласти на множники за формулою:

ax2 + bx + c = a(x - x1)(x - x2 ), де x1 і x2 – корені тричлена.

2x2 -11x + 5 = 0, D =121 - 40 = 81,

x =

11 - 9

, x

1 ö

2x2

-11x + 5

ì0

-11x +

5 = 2(x - 5)ç x -

÷,

lim

2 ø

= í

3x2

-14x - 5 = 0, D =196 + 60 =162 ,

x®5 3x2 -14x - 5

x =

14 -16

= -

, x

= 5,

1 ö

-14x -

5 = 3(x - 5)ç x +

3 ø

2(x - 5)ç x -

2x - 1

= lim

x®5

ö x®5

3x + 1 16

3(x - 5)ç x +

ì0ü

3) Невизначеність виду í ý, якщо вона задана ірраціональними виразами.

î0þ

Правило: необхідно ірраціональність із чисельника(знаменника) перенести в знаменник (чисельник) помноживши на спряжений вираз, спростити, скоротити на критичний множник і знову перейти до границі.

У випадку, якщо маємо

вираз a - b ,

то спряженим до нього є

вираз

так як (

)(

) = a - b ;

спряженим до

- b є

+ b , (

- b)(

+ b) = a - b2 ; так само:

(a -

)(a +

) = a2 - b .

lim

1 -

Приклад. Знайти границю

2 - x

x®1 x2 -1

Розв’язання. Позбавляємось ірраціональності в чисельнику шляхом множення чисельника на 1 + 2 - x . Щоб не змінилось значення відношення, необхідно і знаменник помножити на1 + 2 - x . Далі відношення скорочуємо на критичний множник ( x -1) і переходимо до границі:

lim

2 - x

0 ü

= lim

2 - x)(1 +

2 - x)

= í

x 2

(x 2

- 1)(1 +

x®1

- 1

0 þ x®1

2 - x

)

= lim

1 - 2 + x

= lim

x -1

x®1 (x 2 - 1)(1 +

2 - x

)

x®1

(x - 1)(х + 1)(1 + 2 - x)

= lim

x®1

(х + 1)(1 + 2 - x )

ì0ü

4) Невизначеність виду í ý, якщо вона задана тригонометричними

î0þ

виразами.

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.02.2016301.59 Кб113Magistratura_OGG_95_pitan.docx
#
12.02.20161.84 Mб9mag_8.03050901_bo_12.doc
#
11.02.2016356.86 Кб49mag_8.14010101_grs_2014(2).doc
#
12.02.20167.16 Mб86Makarov_S._Yu._Slavskaya__I._L_._Innovatsii_v_tekhnologii_i_oborudovanii_prigotovleniya_vodok.pdf
#
20.09.201984.95 Кб1Matematika.docx
#
12.02.2016761.1 Кб22matra.rozpaxyhk.pdf
#
10.11.20195.21 Mб45Meetings and Negitiations.doc
#
17.11.2019456.7 Кб6MET-mas-obs.doc
#
14.11.2019607.23 Кб6Method 2011.doc
#
18.11.2019438.27 Кб5metMex-повна.doc
#
23.08.2019951.81 Кб10Metod diplom bakalavr BTMS.doc